Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Flächen und Volumina/Volumina: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 17: | Zeile 17: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
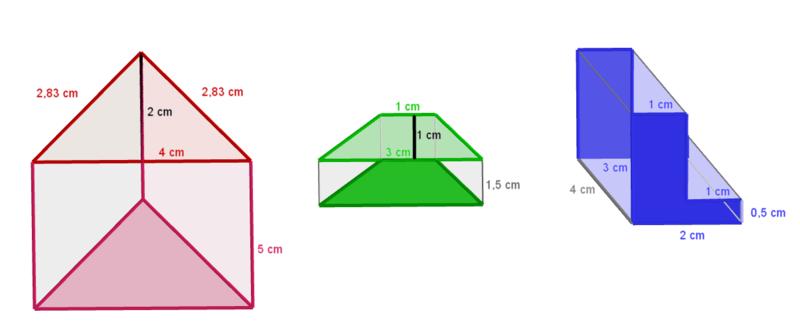
Für alle drei Prismen gilt <math> V= G \cdot h. </math> | Für alle drei Prismen gilt <math> V= G \cdot h. </math> | ||
# Die Grundseite ist ein Dreieck: Es gilt <math> V= G \cdot h = \frac{1}{2} \cdot 4 \cdot 2 \cdot 5 = 4 \cdot 5 =20 </math> [cm<sup>3</sup>]. | |||
|Lösung anzeigen|Lösung verbergen}} | |Lösung anzeigen|Lösung verbergen}} | ||
Version vom 19. April 2020, 11:37 Uhr
Info
Hast du schon mal ein riesiges Paket bekommen, in dem nur ein kleiner Gegenstand enthalten war? Viel Luft und wenig Inhalt? Auf der vorherigen Seite hast du dich bereits mit Verpackungen beschäftigt. Häufig geht es nicht nur um das Material, das eine Verpackung verbraucht, sondern auch den Raum, den eine Verpackung einnimmt bzw. zur Verfügung stellt. Das Volumen eines Quaders oder eines Würfels kannst du bereits berechnen. Auf dieser Seite erfährst du, wie man dieses Wissen nutzen kann, um das Volumen von anderen Prismen oder einem Zylinder zu bestimmen.
Erklärvideo
Erfahre in dem folgenden Video, wie man das Volumen eines Prismas oder eines Zylinders berechnet. Stoppe das Video, wenn es dir an einer Stelle zu schnell geht. Höre dir schwierige Stellen mehrfach an.
Merke
Das Volumen V von Prismen und Zylindern mit der Grundfläche G und der Höhe h berechnet man mit der Formel
Für einen Zylinder mit der Höhe h und dem Radius r der Grundfläche G gilt demnach
Anwendung
Für alle drei Prismen gilt
- Die Grundseite ist ein Dreieck: Es gilt [cm3].
Aufgabe 2
Zeichne einen Zylinder mit dem Durchmesser cm und der Höhe cm in dein Heft. Ermittle das Volumen des Zylinders.
Das Volumen eines Zylinders berechnet sich als Produkt aus Grundfläche und Höhe: [cm3].