Einführung von Funktionen: Unterschied zwischen den Versionen
Markierung: 2017-Quelltext-Bearbeitung |
Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 107: | Zeile 107: | ||
|Lösung zeigen | Lösung verstecken}}|Lösung}} | |Lösung zeigen | Lösung verstecken}}|Lösung}} | ||
{{ | |||
| | {{Fortsetzung|weiter=Funktion - eine eindeutige Zuordnung|weiterlink= Agnes lint/Funktion - eine eindeutige Zuordnung}} | ||
}} | |||
Version vom 26. März 2020, 15:07 Uhr
Einführung von Funktionen
Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.
- FA 1.3: Zwischen tabellarischer und graphischer Darstellung von Funktionen wechseln können
- FA 1.4: Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im Kontext deuten können
Funktionen – was ist das eigentlich genau?
Wir Menschen erkennen und suchen in unserer Welt seit jeher nach Zusammenhängen und versuchen Verbindungen zwischen unterschiedlichsten Ereignissen herzustellen.
So kann etwa ein Zusammenhang wischen der Körpergröße und dem Körpergewicht festgestellt werden. Die Körpergröße ist dabei ursächlich für das Körpergewicht. Im folgenden Lernpfad wirst du erfahren, wie man Zusammenhänge mit sogenannten Funktionen genau beschreiben und graphisch sichtbar machen kann.
Einführung des Funktionsbegriff
Um den vorher bereits besprochenen Zusammenhang zwischen Körpergröße und Gewicht untersuchen zu können, müssen wir zu allererst eine Wertetabelle erstellen. Dabei wird in der ersten Spalte die Körpergröße und in die zweite Spalte das Gewicht eingetragen.
Eine Tabelle, die eine Zuordnung darstellt, nennt man Wertetabelle.
- In der ersten Spalte stehen die Werte der unabhängigen Größe, in der zweiten die der abhängigen.
- Die Einheiten der Größen sollen ebenso angegeben sein.
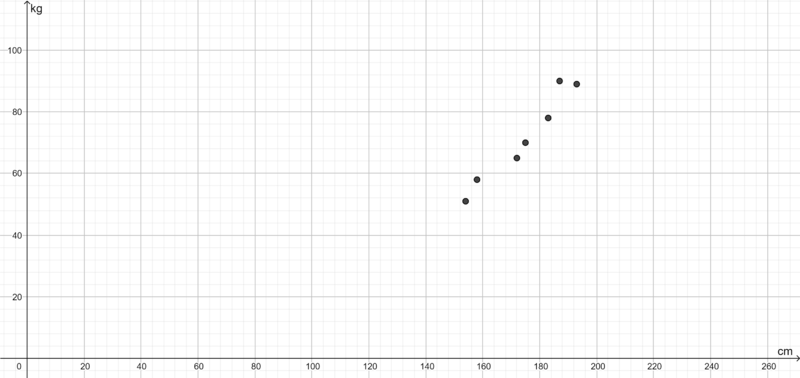
Körpergröße (in cm) Gewicht (in kg) 154 51 158 58 161 57 172 65 178 70 183 78 187 90 193 89
Um den Graphen einer Zuordnung zu erhalten, werden Wertepaare in ein Koordinatensystem eingezeichnet.
- Die unabhängige Variable wird auf die waagrechte Achse (Abszisse) eingetragen, die abhängige Größe in Richtung der senkrechten Achse (Ordinate).
- Die Beschriftung der Achsen ist bei jedem Graphen sehr wichtig. Es muss ersichtlich sein welche Werte auf den einzelnen Achsen aufgetragen werden und in welcher Einheit sie aufgetragen werden.
Um den Zusammenhang zwischen Körpergröße und Körpergewicht graphisch sichtbar zu machen, werden die Wertepaare nun in ein Koordinatensystem eingetragen.
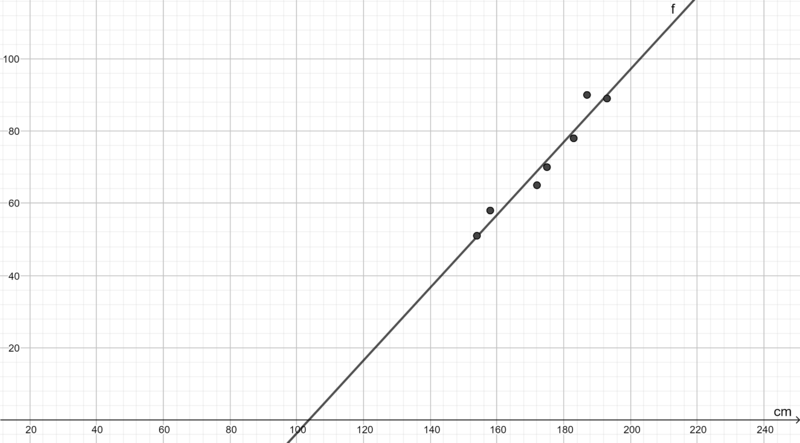
Man erkennt nun, dass die Wertepaare zumindest annähernd auf einer geraden Linie liegen. Natürlich berührt die Linie nicht alle Punkt, allerdings erhält man so eine sogenannte Annäherung.
.png)
Die gerade Linie ergibt also für jeden beliebigen x-Wert einen zugehörigen y-Wert (nicht nur für unsere bereits eingetragenen Punkte.)
Die Termdarstellung drückt den Zusammenhang zwischen zwei Größen in Form einer Gleichung aus. Für diese Darstellungsart ist es unbedingt notwendig, die einzelnen Größen des Zusammenhangs durch Buchstaben zu benennen und mit den dazugehörigen Einheiten klar auszuweisen.
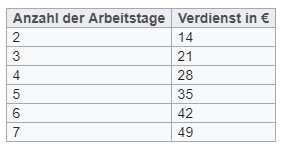
Die Schreibweise f(x) (gesprochen "f von x") drückt aus, dass die Größe f von der unabhängigen Größe x abhängt.Antonia soll ihrer Mutter mindestens zwei und höchstens sieben Tage lang helfen. Sie erhält dafür jeden Tag 7 €. Antonias Verdienst hängt von der Anzahl der Arbeitstage ab.
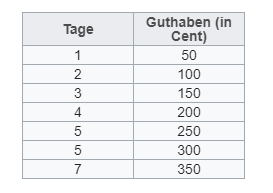
- Erstelle eine Tabelle, die Antonias Verdienst in Abhängigkeit von den Arbeitstagen zeigt.
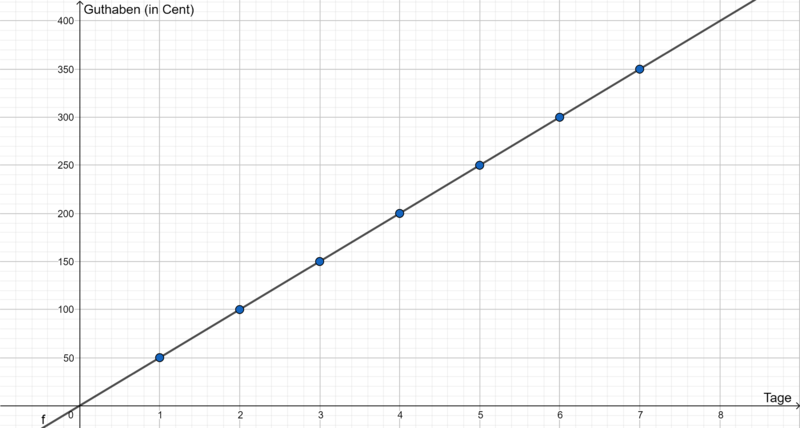
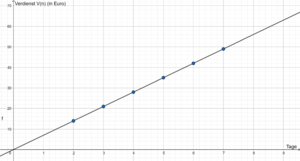
- Zeichne den Graphen der Zuordnung.
- Gib einen Term für die dargestellte Zuordnung an.
Zunächst müssen Variablen für die beiden Größen der Zuordnung gewählt werden. n: Anzahl der Arbeitstage V(n): Verdienst nach n Arbeitstagen in Euro (€)
Termdarstellung:
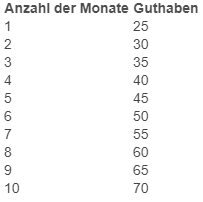
Joshua hat bereits 20€ angespart. Er plant in den nächsten zehn Monaten sein Erspartes jeweils am Monatsende um 5€ zu vermehren.
- Erstelle eine Tabelle, die das monatliche Guthaben in den zehn Monaten darstellt.
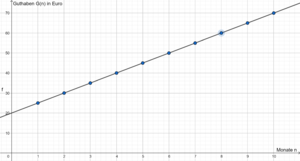
- Zeichne den Graphen der Zuordnung.
- Gib einen Term für die dargestellte Zuordnung an.
Zunächst müssen Variablen für die beiden Größen der Zuordnung gewählt werden. n: Anzahl der Monate G(n): Guthaben nach n Monaten in Euro (€) Termdarstellung:
