Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als Steigung der Tangente: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
==Die Steigung einer Sekante== | ==Die Steigung einer Sekante== | ||
[[Datei:Beispielbild Sekante.png|rand|459x459px]] | [[Datei:Beispielbild Sekante.png|rand|459x459px]] | ||
<br />{{Box|Aufgabe 2|a) Geben Sie die Definition einer Sekante, wie Sie sie im obigen Bild zu sehen ist an. <br/> | <br />{{Box|Aufgabe 2.2|a) Geben Sie die Definition einer Sekante, wie Sie sie im obigen Bild zu sehen ist an. <br/> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1={{Box|Sekante|Eine Sekante ist eine Gerade, die den Graphen einer Funktion in (mindestens) zwei Punkten schneidet.|Merksatz}}|2=Lösung anzeigen|3=Lösung verbergen}} | ||
b) Geben Sie an wie sich die Steigung <math>m</math> einer Sekante der Funktion <math>f</math> durch die Punkte <math>P(x_0|f(x_0))</math> und <math>Q(x|f(x))</math> allgemein berechnen lässt. <br/> | b) Geben Sie an wie sich die Steigung <math>m</math> einer Sekante der Funktion <math>f</math> durch die Punkte <math>P(x_0|f(x_0))</math> und <math>Q(x|f(x))</math> allgemein berechnen lässt. <br/> | ||
{{Lösung versteckt|1=[[Datei:Differerenzenquotient Hilfe.png|rand|600x600px]]|2=Hilfe anzeigen|3=Hilfe verbergen}} | {{Lösung versteckt|1=[[Datei:Differerenzenquotient Hilfe.png|rand|600x600px]]|2=Hilfe anzeigen|3=Hilfe verbergen}} | ||
{{Lösung versteckt|1= | |||
{{Box|Der Differenzenquotient|Die Steigung des Graphen einer linearen Funktion kann mit Hilfe des Differenzenquotienten berechnet werden. | |||
c) Berechnen Sie in | Ist eine Funktion <math>f</math> auf einem Intervall <math>[x_0;x]</math> definiert, so gibt der Differenzenquotient | ||
{{Lösung versteckt|1=Text zum Verstecken|2=Lösung anzeigen|3=Lösung verbergen}} | |||
<math>\frac{\Delta{y}}{\Delta{x}}=\frac{f(x_0)-f(x)}{x_0-x}</math> die Steigung <math>m</math> der Geraden durch die Punkte <math>A=(x_0|f(x_0))</math> und <math>B=(x|f(x))</math> an. | |||
Die Differenzen können auch als <math>\Delta{y} </math>und <math>\Delta{x}</math>geschrieben werden. Der griechische Großbuchstabe Delta steht hier als Symbol für die Differenz der x- und y-Werte. |Merksatz}}|2=Lösung anzeigen|3=Lösung verbergen}} | |||
c) Berechnen Sie in folgender Graphik die Steigung der Sekante durch die Punkte P und Q. <br/> | |||
{{Lösung versteckt|1=Graphik {{Lösung versteckt|1=Hilfe|2=Hilfe anzeigen|3=Hilfe verbergen}}|2=Graphik anzeigen|3=Graphik verbergen}}{{Lösung versteckt|1=Text zum Verstecken|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
==Die Steigung der Tangente== | ==Die Steigung der Tangente== | ||
<br />{{Box|Aufgabe 3|Wir betrachten die Funktion <math>f(x)=x^3+x</math>, den festen Punkt <math>P(x_0|f(x_0))</math> mit <math>x_0=1</math>und den flexiblen Punkt <math>Q(x|f(x))</math>. | <br />{{Box|Aufgabe 2.3|Wir betrachten die Funktion <math>f(x)=x^3+x</math>, den festen Punkt <math>P(x_0|f(x_0))</math> mit <math>x_0=1</math>und den flexiblen Punkt <math>Q(x|f(x))</math>. | ||
<br/> | <br/> | ||
Nähern Sie den Punkt Q in 4 Schritten so nahe wie es das Applet zulässt dem Punkt P. <br/> | Nähern Sie den Punkt Q in 4 Schritten so nahe wie es das Applet zulässt dem Punkt P. <br/> | ||
Halten Sie die Schritte in folgender Tabelle schriftlich fest. Entnehmen Sie die benötigten Werte | Halten Sie die Schritte in folgender Tabelle schriftlich fest. Entnehmen Sie die benötigten Werte [[/Aufgabe 3 a)|<u>diesem Applet</u>]]. | ||
{{Lösung versteckt| | {{Lösung versteckt| Text |2=Lösung anzeigen|3=Lösung verbergen}} | ||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
| Zeile 68: | Zeile 77: | ||
|} | |} | ||
<br /> | <br /> | ||
{{Box|Aufgabe 4| | {{Box|Aufgabe 2.4| | ||
Beschreiben Sie auf was zu achten ist, wenn mit Hilfe der Steigung der Sekante durch zwei Punkte der Funktion die Steigung der Tangente möglichst genau bestimmen will. | Beschreiben Sie auf was zu achten ist, wenn mit Hilfe der Steigung der Sekante durch zwei Punkte der Funktion die Steigung der Tangente möglichst genau bestimmen will. | ||
{{Lösung versteckt|Applets|Applets anzeigen|Applets verbergen}} | {{Lösung versteckt|Applets|Applets anzeigen|Applets verbergen}} | ||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
Aktuelle Version vom 21. August 2019, 10:17 Uhr
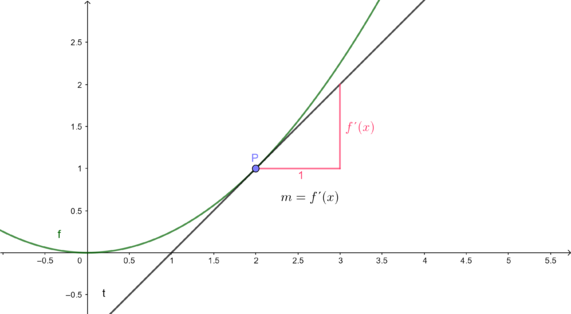
Die Tangente
a) In diesem Applet sehen Sie zwei verschiedene Tangenten. Nennen Sie Unterschiede und Gemeinsamkeiten der beiden Tangenten
b) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie was Sie sehen.
c) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie was Sie sehen.
e) Treffen Sie eine Aussage über die Steigung der Tangente und die Steigung der Funktion im Berührpunkt mit der Tangente.
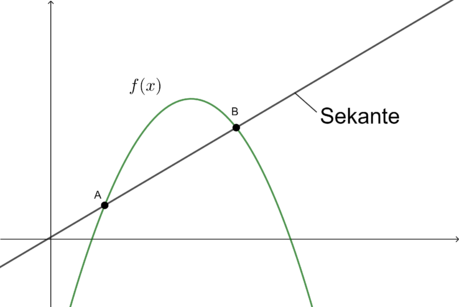
Die Steigung einer Sekante
a) Geben Sie die Definition einer Sekante, wie Sie sie im obigen Bild zu sehen ist an.
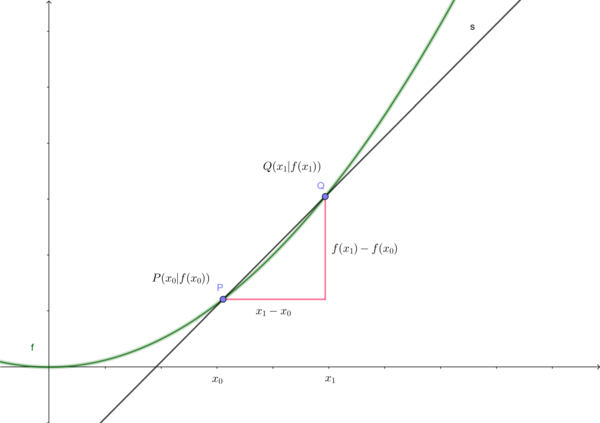
b) Geben Sie an wie sich die Steigung einer Sekante der Funktion durch die Punkte und allgemein berechnen lässt.
Die Steigung des Graphen einer linearen Funktion kann mit Hilfe des Differenzenquotienten berechnet werden.
Ist eine Funktion auf einem Intervall definiert, so gibt der Differenzenquotient
die Steigung der Geraden durch die Punkte und an.
Die Differenzen können auch als und geschrieben werden. Der griechische Großbuchstabe Delta steht hier als Symbol für die Differenz der x- und y-Werte.c) Berechnen Sie in folgender Graphik die Steigung der Sekante durch die Punkte P und Q.
Die Steigung der Tangente
Wir betrachten die Funktion , den festen Punkt mit und den flexiblen Punkt .
Nähern Sie den Punkt Q in 4 Schritten so nahe wie es das Applet zulässt dem Punkt P.
Halten Sie die Schritte in folgender Tabelle schriftlich fest. Entnehmen Sie die benötigten Werte diesem Applet.
| Schritt 1 | |||
| Schritt 2 | |||
| Schritt 3 | |||
| Schritt 4 |
Beschreiben Sie auf was zu achten ist, wenn mit Hilfe der Steigung der Sekante durch zwei Punkte der Funktion die Steigung der Tangente möglichst genau bestimmen will.