Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Zusammenfassung Grundvorstellungen zum Ableitungsbegriff: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 40: | Zeile 40: | ||
==='''Die Ableitung als lokale lineare Approximation'''=== | ==='''Die Ableitung als lokale lineare Approximation'''=== | ||
Um zu erläutern welche Rolle die Ableitung bei der lokalen linearen Approximation einer Funktion einnimmt, wird zunächst geklärt wie | Um zu erläutern welche Rolle die Ableitung bei der lokalen linearen Approximation einer Funktion einnimmt, wird zunächst geklärt wie Funktionen lokal, also in sehr kleinen Umgebungen verhalten. | ||
Zoomt man in verschiedene Funktionen hinein so erkennt man, dass sich Funktionen einerseits lokal linear, also geradlinig oder oder andererseits nicht linear verhalten können (Aufgabe ??). | Zoomt man in verschiedene Funktionen hinein so erkennt man, dass sich Funktionen einerseits lokal linear, also geradlinig oder oder andererseits nicht linear verhalten können (Aufgabe ??). | ||
Verhält sich eine | Verhält sich eine Funktion <math>f</math>um eine Stelle <math>x_0</math>lokal linear, so existiert an dieser Stelle auch die Ableitung <math>f'(x_0)</math>. {{Lösung versteckt|Da sich in einem lokal linearen Teilausschnitt des Graphen um <math>x_0</math> der Abstand zwischen <math>x_0</math> und einem <math>x_1</math> durch nähern von <math>x_1</math> an <math>x_0</math> beliebig stark verkleinern lässt, existiert der Grenzwert des Differenzenquotienten und die Funktion <math>f</math> besitzt an der Stelle <math>x_0</math> eine Ableitung. |genauer erklärt|ausblenden}} | ||
Der Graph der Linearisierung der Funktion <math>f</math>um die Stelle <math>x_0</math>ist dann die Tangente von <math>f</math>an der Stelle <math>x_0</math>. | Der Graph der Linearisierung der Funktion <math>f</math>um die Stelle <math>x_0</math>ist dann die Tangente von <math>f</math>an der Stelle <math>x_0</math>. | ||
Da sich Tangente und Funktionsgraph in einer hinreichend kleinen Umgebung kaum unterscheiden, spricht man von einer lokal linearen Approximation. | Da sich Tangente und Funktionsgraph in einer hinreichend kleinen Umgebung kaum unterscheiden, spricht man von einer '''lokal linearen Approximation'''. | ||
Durch diese Linearisierung der Funktion um die Stelle <math>x_0</math>lassen sich demzufolge auch andere x-Werte nähern. | Durch diese Linearisierung der Funktion um die Stelle <math>x_0</math>lassen sich demzufolge auch andere x-Werte nähern. Diese Näherungen lassen sich wie folgt ausdrücken. | ||
<math>f(x)=f(x_0)+f'(x_0)(x-x_0 | <math>f(\tilde{x})=f(x_0)+f'(x_0)(x-x_0) </math> | ||
[[Datei:Lokal lineare Approximation.png|alternativtext=|links|mini|350x350px]] | |||
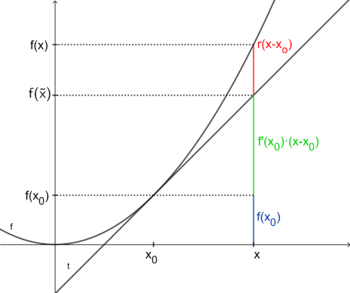
Wie zu erkennen ist setzt sich ein durch die Tangente approximierter x-Wert aus den in der Abbildung farblich gekennzeichneten Summanden zusammen. <math> | |||
Wie zu erkennen ist, setzt sich ein durch die Tangente approximierter x-Wert aus den in der Abbildung farblich gekennzeichneten Summanden zusammen. <math>r(x-x_0)</math>ist die Differenz zwischen Funktion und Tangente und lässt sich als Approximationfehler interpretieren. Je näher der approximierte x-Wert der Stelle <math>x_0</math>kommt, desto kleiner wird der Approximationsfehler und umso genauer wird die Näherung durch die Tangente. {{Lösung versteckt|kommt noch |mehr zum Approximationsfehler |ausblenden}} | |||
Aktuelle Version vom 20. August 2019, 13:52 Uhr
Auf dieser Seite finden Sie die Grundvorstellungen, die Sie sich in diesem Lernpfad selbst erschließen können in einer detaillierten Zusammenfassung. Die Zusammenfassung können Sie auch als PDF oder Word Dokument herunterladen.
Die Ableitung
Im folgender werden vier Grundvorstellungen zur Ableitung erläutert. Es ist zu beachten, dass sich aufgrund der Überschneidungen und Ergänzungen die Grundvorstellungen nicht isoliert zu betrachten sind.
Diese Definition kann mit folgenden Grundvorstellungen interpretiert und gedeutet werden.
Die Ableitung als lokale (momentane) Änderungsrate
Die Grundvorstellung der Ableitung als lokale oder auch momentane Änderungsrate baut auf dem Verständnis von Änderungsprozessen auf, die bereits in der Sekundarstufe 1 behandelt wurden. Es wird nun also neben der absoluten Änderung und der mittleren (durchschnittlichen) Änderungsrate auch die lokale Änderungsrate beschrieben.
Wie auch in der Bearbeitung des Lernpfades lässt sich diese Grundvorstellung am besten über einen Weg-Zeit-Zusammenhang erschließen.
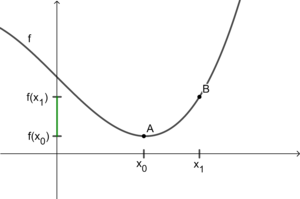
So entspricht im Kontext eines Weg-Zeit-Zusammenhangs die absolute Änderung der Wegzunahme vom Zeitpunkt bis und die mittlere Änderungsrate der mittleren (durchschnittlichen) Geschwindigkeit im Intervall . Da sich die mittlere Änderungsrate über ein Steigungsdreieck, also über den Differenzenquotienten berechnen lässt, ist sie graphisch mit der Steigung der Sekante zu deuten.
Durch sukzessive Verkleinerung dieses Intervalls, beispielsweise durch die Näherung von an , lässt sich dann der genäherten Stelle eine lokale (momentane) Änderungsrate zuschreiben, die der momentanen Geschwindigkeit entspricht. Die Verkleinerung des Intervalls kann sowohl tabellarisch (siehe Aufgabe ??) als auch graphisch-dynamisch (siehe Aufgabe ??) erfolgen. Die lokale Änderungsrate ist dementsprechend graphisch als die Steigung des Graphen an der Stelle , also der Steigung der Tangente im Berührpunkt zu interpretieren.
Die Ableitung als Steigung der Tangente
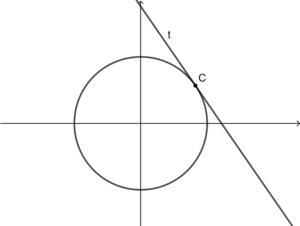
Wie der Name schon sagt, ist bei dieser Grundvorstellung die Ableitung als Steigung der Tangente zu interpretieren. Es gilt also die bereits vorhandene Vorstellung der Tangente, die im Zusammenhang mit Kreisen erworben wurde, auf das Analytische zu erweitern.
In der Kreisgeometrie der Sekundarstufe 1 wurde die Tangente als eine Gerade definiert, die genau einen gemeinsamen Punkt (Berührpunkt) mit dem Kreis hat. In der Analysis hingegen ist die Tangente von an der Stelle die Gerade, die den Graphen von in einem Punkt berührt und die gleiche Steigung wie der Graph von an dieser Stelle hat.
Die Ableitung entspricht also der Steigung von an der Stelle und ebenso der Steigung der Tangente von an der Stelle . Veranschaulichen lässt sich dies durch das Funktionenmikroskop (Aufgabe ??), das bei starkem Hineinzoomen in einen Graph zeigt wie sich die Tangente an den Graphen anschmiegt und letztlich nicht mehr von ihm zu unterscheiden ist.
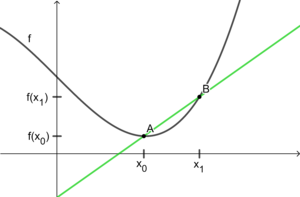
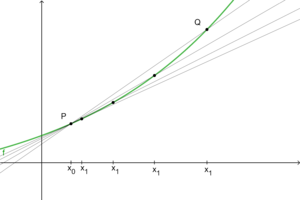
Hergeleitet wird die Ableitung, also die Steigung der Tangente bei dieser Grundvorstellung über die Steigung von Sekanten. Die Steigung der Sekante durch zwei Punkte und eines Funktionsgraphen kann mittels Steigungsdreieck und Differenzenquotienten leicht berechnet werden. Lässt man nun den Abstand zwischen und durch nähern von an immer kleiner werden, so erhält man die Steigung die der Graph in diesem endlos verkleinerbaren Intervall hat. Es entsteht also letztendlich die punktuelle Steigung des Graphen an der Stelle . Graphisch-dynamisch lässt sich dies durch die Näherung des Punktes an den Punkt visualisieren (Aufgabe ??).
Es entsteht eine Gerade, die den Graphen lediglich berührt und die gleiche Steigung wie der Graph im Punkt , also an der Stelle hat. Die Tangente. Als die Steigung der Tangente ergibt sich somit der Grenzwert des Differenzenquotienten , die Ableitung .
Die Ableitung als lokale lineare Approximation
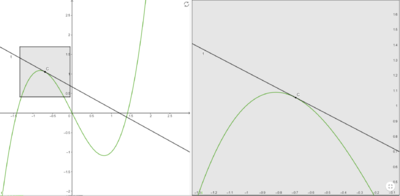
Um zu erläutern welche Rolle die Ableitung bei der lokalen linearen Approximation einer Funktion einnimmt, wird zunächst geklärt wie Funktionen lokal, also in sehr kleinen Umgebungen verhalten.
Zoomt man in verschiedene Funktionen hinein so erkennt man, dass sich Funktionen einerseits lokal linear, also geradlinig oder oder andererseits nicht linear verhalten können (Aufgabe ??).
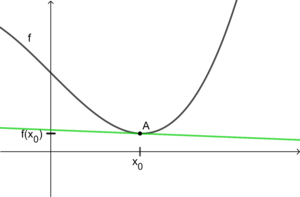
Verhält sich eine Funktion um eine Stelle lokal linear, so existiert an dieser Stelle auch die Ableitung .
Der Graph der Linearisierung der Funktion um die Stelle ist dann die Tangente von an der Stelle .
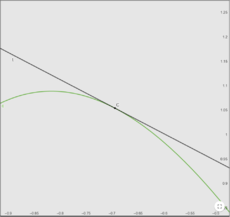
Da sich Tangente und Funktionsgraph in einer hinreichend kleinen Umgebung kaum unterscheiden, spricht man von einer lokal linearen Approximation.
Durch diese Linearisierung der Funktion um die Stelle lassen sich demzufolge auch andere x-Werte nähern. Diese Näherungen lassen sich wie folgt ausdrücken.
Wie zu erkennen ist, setzt sich ein durch die Tangente approximierter x-Wert aus den in der Abbildung farblich gekennzeichneten Summanden zusammen. ist die Differenz zwischen Funktion und Tangente und lässt sich als Approximationfehler interpretieren. Je näher der approximierte x-Wert der Stelle kommt, desto kleiner wird der Approximationsfehler und umso genauer wird die Näherung durch die Tangente.