Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Vorwissen: Unterschied zwischen den Versionen
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br />{{Box|Info|Auf dieser Seite werden alle Voraussetzung wiederholt, die Sie zur Bearbeitung des Lernpfades benötigen. | {{Navigation verstecken|{{Vorlage:Lernpfad-Navigation| | ||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Vorwissen|Vorwissen]]<br/> | |||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale Änderungsrate|Die Ableitung als lokale Änderungsrate]] <br/> | |||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als Steigung der Tangente|Die Ableitung als Steigung der Tangente]]<br/> | |||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale lineare Approximation|Die Ableitung als lokale lineare Approximation]]<br/> | |||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Zusammenfassung Grundvorstellungen zum Ableitungsbegriff|Zusammenfassung Grundvorstellungen zum Ableitungsbegriff]] | |||
[[Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Infos für Lehrkräfte|Infos für Lehrkräfte]]}}}}<br /> | |||
{{Box|Info|Auf dieser Seite werden alle Voraussetzung wiederholt, die Sie zur Bearbeitung des Lernpfades benötigen. | |||
Das Vorwissen steht Ihnen auch als PDF zur Verfügung. |Kurzinfo | Das Vorwissen steht Ihnen auch als PDF zur Verfügung. |Kurzinfo | ||
}} | }} | ||
| Zeile 7: | Zeile 14: | ||
==='''Sekanten an Funktionsgraphen'''=== | ==='''Sekanten an Funktionsgraphen'''=== | ||
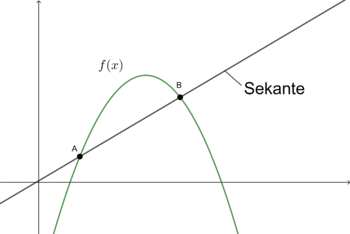
Eine Sekante ist eine Gerade, die den Graphen einer Funktion in zwei Punkten schneidet. | Eine Sekante ist eine Gerade, die den Graphen einer Funktion in (mindestens) zwei Punkten schneidet. | ||
[[Datei:Beispielbild Sekante.png|mini|350x350px|Sekante des Funktionsgraphen <math>f(x) | [[Datei:Beispielbild Sekante.png|mini|350x350px|Sekante des Funktionsgraphen <math>f(x) | ||
</math> durch die Punkte <math>A</math> und <math>B</math>.|alternativtext=|ohne]] | </math> durch die Punkte <math>A</math> und <math>B</math>.|alternativtext=|ohne]] | ||
| Zeile 29: | Zeile 36: | ||
===='''Die h - Schreibweise'''==== | ===='''Die h - Schreibweise'''==== | ||
Anstatt die Änderung der y-Werte <math>\Delta{y}=f(x_1)-f(x_0)</math> in Relation zur Differenz <math>\Delta{x}=x_1-x_0</math> zu setzen, kann man den Differenzenquotienten auch wie folgt schreiben: <math>\frac{f(x_0+h)-f(x_0)}{h}</math> | Anstatt die Änderung der y-Werte <math>\Delta{y}=f(x_1)-f(x_0)</math> in Relation zur Differenz <math>\Delta{x}=x_1-x_0</math> zu setzen, kann man den Differenzenquotienten auch wie folgt schreiben: <math>\frac{f(x_0+h)-f(x_0)}{h}</math> | ||
[[Datei:H-Methode_Diff.png|verweis=https://unterrichten.zum.de/wiki/Datei:H-Methode_Diff.png|alternativtext=|rand|zentriert|450x450px]] | [[Datei:H-Methode_Diff.png|verweis=https://unterrichten.zum.de/wiki/Datei:H-Methode_Diff.png|alternativtext=|rand|zentriert|450x450px]]<br /> | ||
==='''Änderungsprozesse'''=== | |||
In folgender Tabelle sind mehrere Beispiele illustriert, die Ihnen Szenarien aufzeigen, deren absolute und mittlere Änderungen Sie bereits mit dem Wissen aus der Sekundarstufe 1 beschreiben können. | |||
{| class="wikitable" | {| class="wikitable" | ||
|+Beispiele für Bestandsgrößen und deren Änderungen | |+Beispiele für Bestandsgrößen und deren Änderungen | ||
| Zeile 62: | Zeile 67: | ||
|} | |} | ||
=====''' | <br /> | ||
[[Datei: | |||
Bei einem Experiment wurde die Temperatur einer Flüssigkeit in 10 Minuten Abständen gemessen. Die mittlere Änderungsrate der Temperatur lässt sich nun mit Hilfe des Differenzenquotient berechnen | ===='''Die absolute Änderung'''==== | ||
Die absolute Änderung ist die Änderung <math>f(x_1)-f(x_0) </math>eines Bestandes vom Zeitpunkt (oder einer anderen unabhängigen die sich auf den Bestand auswirkt) <math>x_1-x_0</math>. | |||
===='''Die mittlere Änderungsrate'''==== | |||
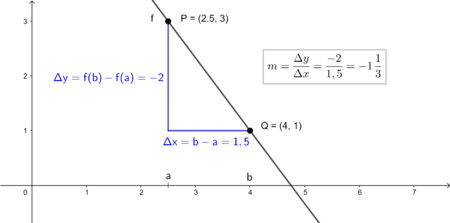
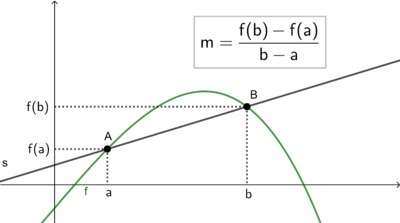
Die mittlere (durchschnittliche) Änderungsrate ist die relative Änderung eines Bestandes in einem gegebenen Intervall. Sie entspricht der Steigung <math>m</math>der Sekante durch die Punkte <math>A=(a|f(a))</math> und <math>B=(b|f(b))</math> der Bestandsfunktion <math>f</math> und lässt sich mit Hilfe des Differenzenquotienten berechnen. | |||
[[Datei:Mittlere Änderungsrate als Sekantensteigung .png|alternativtext=|ohne|mini|400x400px|Bestandsfunktion f und die mittlere Änderungsrate im Intervall [a,b] als Steigung der Sekante durch die Punkte A und B.]] | |||
<br /> | |||
{| class="wikitable" | |||
|+ | |||
Beispiele für mittlere Änderungsraten | |||
!unabhängige Größe | |||
!abhängige Größe | |||
!mittlere Änderungsrate | |||
|- | |||
|Zeit | |||
|Wegstrecke | |||
|Durchschnittsgeschwindigkeit | |||
|- | |||
|Zeit | |||
|Geschwindigkeit | |||
|Mittlere Beschleunigung | |||
|- | |||
|Zeit | |||
|Wassermenge in einem Becken | |||
|mittlere Zuflussgeschwindigkeit | |||
|} | |||
====='''Beispiel: Wassertemperatur'''===== | |||
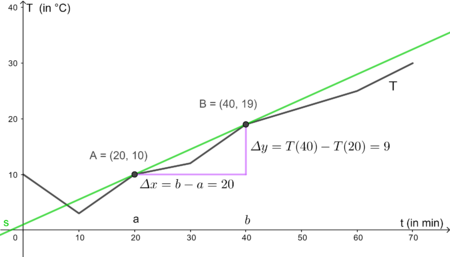
[[Datei:Differenzenquotient Temp.png|mini|450x450px|Bestandsfunktion <math>T(x)</math>]] | |||
Bei einem Experiment wurde die Temperatur einer Flüssigkeit in 10 Minuten Abständen gemessen. Die mittlere Änderungsrate der Temperatur im Intervall <math>[a;b]</math>lässt sich nun mit Hilfe des Differenzenquotient berechnen. | |||
<math>\frac{\Delta{y}}{\Delta{x}}=\frac{T(b)-T(a)}{b-a}=\frac{9 C}{20 min}=0,45\frac{C}{min}</math> | <math>\frac{\Delta{y}}{\Delta{x}}=\frac{T(b)-T(a)}{b-a}=\frac{9 C}{20 min}=0,45\frac{C}{min}</math> | ||
Von der zwanzigsten bis zur vierzigsten Minute nimmt die Temperatur also im durchschnitt 0,45 Grad Celsius pro Minute zu. Für die Steigung der Sekante durch die Punkte <math>A=(a|T(a))</math>und <math>B=(b|T(b))</math> gilt in dementsprechend <math>m=0,45</math>. | |||
Aktuelle Version vom 20. August 2019, 16:11 Uhr
Auf dieser Seite werden alle Voraussetzung wiederholt, die Sie zur Bearbeitung des Lernpfades benötigen.
Das Vorwissen steht Ihnen auch als PDF zur Verfügung.
Bild mit Wiederholung einfügen
Sekanten an Funktionsgraphen
Eine Sekante ist eine Gerade, die den Graphen einer Funktion in (mindestens) zwei Punkten schneidet.
Lineare Funktionen
Lineare Funktion sind Funktionen, die eine Funktionsgleichung der Form oder haben. Der Graph einer linearen Funktion ist eine Gerade. Die Zahl gibt den Wert der Steigung an und die Zahl gibt den y-Wert des Schnittpunkts der Geraden mit der y-Achse an.
Der Differenzenquotient
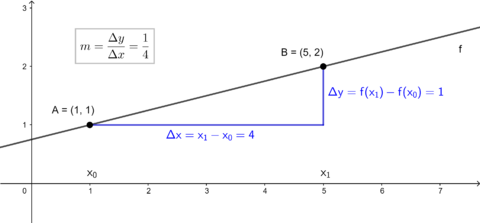
Die Steigung des Graphen einer linearen Funktion kann mit Hilfe des Differenzenquotienten berechnet werden.
Ist eine Funktion auf einem Intervall definiert, so gibt der Differenzenquotient
die Steigung der Geraden durch die Punkte und an.
Die Differenzen können auch als und geschrieben werden. Der griechische Großbuchstabe Delta steht hier als Symbol für die Differenz der x- und y-Werte.
Beispiele
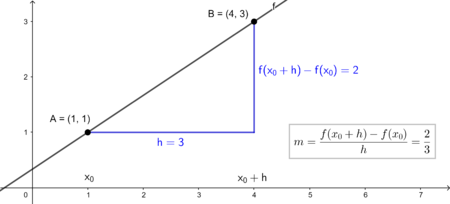
Die h - Schreibweise
Anstatt die Änderung der y-Werte in Relation zur Differenz zu setzen, kann man den Differenzenquotienten auch wie folgt schreiben:
Änderungsprozesse
In folgender Tabelle sind mehrere Beispiele illustriert, die Ihnen Szenarien aufzeigen, deren absolute und mittlere Änderungen Sie bereits mit dem Wissen aus der Sekundarstufe 1 beschreiben können.
| Bestandsgröße | Zuflüsse | Abflüse |
|---|---|---|
| Anzahl der Schüler | Einschulungen | Schulabgänger |
| Treibstoffmenge im Tank | Tanken an der Tankstelle | Treibstoffverbrauch |
| Kontostand | Zubuchung | Abbuchung |
| Anzahl der Hotelgäste | ankommende Gäste | abreisende Gäste |
| Staatsverschuldung | Staatseinnahmen | Staatsausgaben |
Die absolute Änderung
Die absolute Änderung ist die Änderung eines Bestandes vom Zeitpunkt (oder einer anderen unabhängigen die sich auf den Bestand auswirkt) .
Die mittlere Änderungsrate
Die mittlere (durchschnittliche) Änderungsrate ist die relative Änderung eines Bestandes in einem gegebenen Intervall. Sie entspricht der Steigung der Sekante durch die Punkte und der Bestandsfunktion und lässt sich mit Hilfe des Differenzenquotienten berechnen.
| unabhängige Größe | abhängige Größe | mittlere Änderungsrate |
|---|---|---|
| Zeit | Wegstrecke | Durchschnittsgeschwindigkeit |
| Zeit | Geschwindigkeit | Mittlere Beschleunigung |
| Zeit | Wassermenge in einem Becken | mittlere Zuflussgeschwindigkeit |
Beispiel: Wassertemperatur
Bei einem Experiment wurde die Temperatur einer Flüssigkeit in 10 Minuten Abständen gemessen. Die mittlere Änderungsrate der Temperatur im Intervall lässt sich nun mit Hilfe des Differenzenquotient berechnen.
Von der zwanzigsten bis zur vierzigsten Minute nimmt die Temperatur also im durchschnitt 0,45 Grad Celsius pro Minute zu. Für die Steigung der Sekante durch die Punkte und gilt in dementsprechend .