Anwendungsbezogene Extremwertaufgaben: Unterschied zwischen den Versionen
Main>Joerg Stadlinger |
Keine Bearbeitungszusammenfassung |
||
| (183 dazwischenliegende Versionen von 10 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad | __NOTOC__ | ||
{{Box|1=Lernpfad|2= | |||
Üben, Anwenden und Veranschaulichung von Extremwertaufgaben an anwendungsbezogenen Beispielen. | |||
*'''Voraussetzung: '''Kenntnisse über die Ableitungsfunktion und die Bestimmung von Extremwerten | |||
*'''Zeitbedarf:''' eine Unterrichtsstunde/mehrere Unterrichtsstunden | *'''Zeitbedarf:''' eine Unterrichtsstunde/mehrere Unterrichtsstunden | ||
*'''Material:''' Stift und Papier, Konzentration | *'''Material:''' Stift und Papier, Konzentration | ||
}} | [[Datei:Logo Mathematik-digital 2011.png|200px|right|verweis=Mathematik-digital|Mathematik-digital]] | ||
|3=Lernpfad}} | |||
==Einführung== | |||
Willkommen zum Lernpfad "Anwendungsbezogene Extremwertaufgaben". Hier findet ihr Aufgaben, in denen die Bestimmung von Extremwerten anhand von Beispielen aus dem Alltag eingeübt und vertieft werden kann. | |||
'''Kurz zur Wiederholung:''' | |||
Ein Extremwert ist der größte bzw. kleinste Wert einer Funktion (in einem gewissen Bereich). Hier kannst du dir nochmal die formale Definition eines Extremwerts einblenden. | |||
{{Lösung versteckt| | |||
[[Bild:Einführungsgrafik4.png|right|200px]] | |||
Es sei <math> U \subseteq\mathbb R </math> eine Teilmenge der Reellen Zahlen (z.B. ein Intervall) und <math> f\colon U\to\mathbb R </math> eine Funktion. | Es sei <math> U \subseteq\mathbb R </math> eine Teilmenge der Reellen Zahlen (z.B. ein Intervall) und <math> f\colon U\to\mathbb R </math> eine Funktion. | ||
f hat an der Stelle <math> x_0\in U </math> | f hat an der Stelle <math> x_0\in U </math> | ||
| Zeile 24: | Zeile 30: | ||
* ein lokales Maximum, wenn es ein Intervall <math> I = (a,b) </math> gibt, das <math> x_0 </math> enthält, so dass <math> f(x_0)\geq f(x) </math> für alle <math> x\in I\cap U </math> gilt; | * ein lokales Maximum, wenn es ein Intervall <math> I = (a,b) </math> gibt, das <math> x_0 </math> enthält, so dass <math> f(x_0)\geq f(x) </math> für alle <math> x\in I\cap U </math> gilt; | ||
* ein globales Maximum, wenn <math> f(x_0)\geq f(x) </math> für alle <math> x\in U </math> gilt. | * ein globales Maximum, wenn <math> f(x_0)\geq f(x) </math> für alle <math> x\in U </math> gilt.|2=Definition einblenden|3=Definition ausblenden}} | ||
Um diesen Wert zu finden, ist es sinnvoll die Ableitung der Funktion näher zu betrachten. Diese beschreibt nämlich anschaulich die Steigung einer angelegten Tangente an der ursprünglichen Funktion. Bei einem Extremwert, ist diese Tangente waagrecht, d.h. die Ableitungsfunktion an dieser Stelle ist Null. | |||
Diesen Sachverhalt kannst du dir nochmal in folgender Skizze näher anschauen: | |||
<ggb_applet width="805" height="469" version="4.2" id="wfwmyqtg" showreseticon="false" enablerightclick="false" errordialogsactive="true" enablelabeldrags="false" showmenubar="false" showtoolbar="false" showtoolbarhelp="false" showalgebrainput="false" usebrowserforjs="true" allowrescaling="true" /> | |||
Du siehst hier die Funktion <math>a \cdot x^3 + b \cdot x^2 + c \cdot x + d</math>, an der du die Werte a, b, c und d verändern kannst. Wie du siehst, gibt es an bestimmten Stellen maximale und minimale Werte. Betrachte nun folgende Aspekte: | |||
*Welchen Einfluss haben die Parameter a, b, c und d auf die Funktion? Wo liegen die Unterschiede? | |||
*Wo befinden sich die Maxima und Minima der Funktion | |||
*Blende die Ableitungsfunktion ein. Welchen Zusammenhang siehst du? Wie ändert sich die Ableitung mit der Veränderung von a, b, c und d? Was erkennst du bei der Änderung von d? | |||
*Um den Zusammenhang deutlicher zu sehen, klicke auf das Kontrollkästchen Extremwerte | |||
==Wozu überhaupt Extremwerte?== | |||
Extremwerte geben maximale bzw. minimale Größen bei vorgegebenen Randbedingungen an und sind Lösungen bei sogenannten Optimierungsproblemen, d.h. sie geben den idealen Zusammenhang der Funktionsgrößen wieder. Im folgenden soll dies an drei Beispielen verdeutlicht werden. Als erstes wollen wir untersuchen, auf welchem Weg ein Ziel am schnellsten erreicht werden kann (dies ist nicht immer der direkteste Weg). Danach schauen wir uns an, wie man eine größtmögliche Schachtel aus vorgegebenen Karton basteln kann. Als letztes soll untersucht werden, in welchem Winkel man einen Ball werfen muss, um damit eine maximale Wurfweite zu erzielen. | |||
Dies ist ein Ausschnitt aus einem breiten Anwendungsbereich von Extremwertaufgaben bzw. der Differentialrechnung. Denn auch in der Natur werden meist Zustände angenommen, die minimale Energie benötigen und somit über Extremwertbestimmungen ermittelt werden könne. | |||
Nun aber zu unseren Aufgaben... | |||
==Beispiele für anwendungsbezogene Extremwertaufgaben (mit Lösungsanleitung)== | |||
===Extremwertaufgabe mit Nebenbedingung: Der schnellste Weg=== | |||
{{Box|1=Aufgabe 1|2= | |||
[[Bild:AckerStraße2.jpg|left|133px]] | |||
Ein Acker liegt an einer geradlinigen Straße. Ein Fußgänger befindet sich auf dem Acker im Punkt A und möchte möglichst schnell zu einem Punkt B auf der Straße gelangen. Der Fußpunkt C des Lotes von A auf die Straße hat von A die Entfernung 400m und die Entfernung B nach C betrage | |||
(a.) 1000m | |||
(b.) 100m. | |||
Auf der Straße kann sich der Fußgänger doppelt so schnell fortbewegen wie auf dem Acker. Welchen Weg soll er einschlagen? | |||
|3=Arbeitsmethode}} | |||
{{Achtung|Versuche zuerst die Aufgabe ohne Hilfestellung zu lösen!}} | |||
'''Hilfestellung:''' | |||
'''1. Stelle die Aufgabensituation in einer Skizze dar (Teilaufgabe a))''': | |||
Beschrifte, was gegeben und gesucht ist. Gebe den Bekannten und Unbekannten passende Namen. | |||
{{Lösung versteckt|Hier kannst die die Aufgabensituation in einer Skizze betrachten (links der y-Achse im Koordinatensystem) und nebenstehend den Graphen der zu minimierenden Funktion f in der Variablen d (rechts der y-Achse im Koordinatensystem). Diese Funktion f musst du nachher noch bestimmen. | |||
Indem du den Punkt D verschiebst, ändert sich d und somit auch der Funktionswert f(d), was zu dem rechten Graphen führt (grüne Spur). | |||
Bevor wir zur Extremwertberechnung kommen, hier einige Vorüberlegungen: | |||
* Verschiebe den Punkt D und betrachte den nebenstehenden Graphen (grün)! | |||
* Bei welchem Wert d wird der Funktionswert von f minimal? Lese den Wert näherungsweise an der x-Achse bzw. an der Anzeige der Streckenlänge d ab. | |||
* Wie groß sind jeweils die Streckenlängen auf dem Acker a (braune Linie)und der Straße (rote Linie)? Wie kann man diese berechnen? | |||
Notiere deine Gedanken und überprüfe später diese Werte durch die genaue Berechnung des Extremwertes und somit der Streckenlängen, die auf dem Acker und der Straße zurückgelegt werden müssen. | |||
<ggb_applet width="900" height="500" id="admpmehu" showResetIcon="true" /> | |||
}} | |||
'''2. Zielfunktion für Teilaufgabe a)''' : | |||
Erkenne die Zielfunktion und formuliere sie als mathematische Funktion in Abhängigkeit von den Ausgangsgrößen und Unbekannten. | |||
{{Lösung versteckt|Der Weg des Fußgängers setzt sich aus 2 Teilstrecken zusammen, nämlich aus einem geraden Weg über den Acker von A nach D (D liegt auf der Straße), also Strecke a (braune Linie), und dem Teilstück b (rote Linie) von D nach B auf der Straße. | |||
* Sei d der Abstand von C (Fußpunkt des Lotes durch A auf die Straße) und D, wobei <math>0 \le d \le 1000</math> . | |||
* Die Länge des Weges von D nach C, also die rote Strecke b, ist 1000 - d. | |||
* Da der Fußgänger auf dem Acker nur halb so schnell voran kommt wie auf der Straße, müssen die dort zurückzulegenden Meter doppelt gezählt werden. | |||
Die Überlegungen führen uns zu folgender '''Zielfunktion''': | |||
<math>f(x)=2*a+(1000-d)</math> | |||
Diese ist zu minimieren. | |||
}} | |||
'''3. Nebenbedingung in Zielfunktion für Teilaufgabe a)''': | |||
Erkenne die Nebenbedingung, die unabhängige Größen der Zielfunktion zueinander in Beziehung setzt, formuliere sie als mathematischen Ausdruck und setze sie in die Zielfunktion so ein, dass eine äquivalente Zielfunktion für den zu optimierenden Wert in Abhängigkeit von nur einer Variablen entsteht. | |||
{{Lösung versteckt|Die Länge des Weges a von A nach D ist nach Pythagoras <math>a=\sqrt{400^2+d^2}</math> . | |||
Mit dieser Nebenbedingung <math>a=\sqrt{400^2+d^2}</math> ergibt sich durch Ersetzen von a in der [[Mathematik-digital/Testlernpfad Hofmeier/Zielfunktion|Zielfunktion]]: | |||
''' <math>f(d)=2*\sqrt{400^2+d^2}+ (1000-d)= min!</math>''' | |||
}} | |||
'''4. Bestimmung des Extremwertes der Zielfunktion für Teilaufgabe a) und b):''' | |||
Bestimmung des Extremwertes durch Nullsetzen der ersten Ableitung und Überprüfung des Vorzeichens der zweiten Ableitung. | |||
{{Lösung versteckt|1= | |||
'''Teilaufgabe a)''' | |||
* Um den Extremwert der Zielfunktion bzw. den schnellsten Weg, um von A nach B zu kommen, zu bestimmen, benötigen wir die erste Ableitung dieser Funktion, die wir gleich 0 setzen, also <math>f'(d)=0</math>: | |||
<math>f'(d)=(2d/\sqrt{400^2+d^2})-1=0</math> | |||
* Durch Auflösen dieser Bedingung nach d erhält man als Lösung | |||
<math>d=\sqrt{\frac{400^2}{3}}\approx230.94</math> | |||
* Um nachzuprüfen, ob an dieser Stelle ein lokales Minimum (schnellster Weg) vorliegt, berechnen wir die zweite Ableitung der Zielfunktion f<nowiki>''</nowiki>(d) und prüfen, ob durch Einsetzen von unserer Lösung in f<nowiki>''</nowiki>(d) eine Zahl größer als 0 vorliegt, also ob f<nowiki>''</nowiki>(d)>0: | |||
Es gilt <math>f''(d)=[2*\sqrt{400^2+d^2}-d^2/\sqrt{400^2+d^2}]/(400^2+d^2)</math> | |||
und somit <math>f''(\sqrt{\frac{400^2}{3}})>0</math> | |||
* Die Weglänge über die Straße, also die Entfernung von Punkt D zu B, beträgt also | |||
<math>1000-\sqrt{\frac{400^2}{3}}\approx769.04</math>. | |||
Die Weglänge über den Acker beträgt | |||
<math>a=\sqrt{400^2+\sqrt{400^2/3} }\approx461.8</math>. | |||
'''Teilaufgabe b)''' | |||
* Wenn allerdings der Abstand zwischen B und C nur 100m beträgt, so lautet die zu minimierende Zielfunktion | |||
<math>f(d)=2*\sqrt{400^2+d^2}+(100-d)</math> | |||
* Die Ableitung hiervon ist die gleiche wie in Teilaufgabe a) schon betrachtet: | |||
' | <math>f'(d)=(2d/\sqrt{400^2+d^2})-1</math>. | ||
Setzt man diese Ableitung gleich 0, so hat sie für <math>0\le d\le100</math> keine Nullstelle bzw. keine Lösung. Hiermit gibt es in diesem Fall kein lokales Minimum. Die Funktion ist im Intervall [0,100] also streng monoton, weshalb der minimale Wert am Rand des Definitionsbereiches liegen muss, also entweder bei <math>d=0</math> oder bei <math>d=100</math>. | |||
* Durch Einsetzen von d = 0 erhält man <math>f (0)=2*400+100=900</math> | |||
== | Durch Einsetzen von d = 100 erhält man <math>f (100)=2*412+100-100=824</math> | ||
Da der Funktionswert für d=100 der kleinere ist, führt folglich der kürzeste Weg von A nach B auf gerader Linie direkt über den Acker. | |||
}} | |||
<math> x( | ===Bastelstunde: Falten einer Schachtel=== | ||
{{Box|1=Aufgabe 2|2= | |||
Von einem rechteckigen Karton mit Seitenlängen '''a''' und '''b''' (mit '''b''' <math>\le</math> '''a''') schneidet man an den Ecken Quadrate der Seitenlänge '''x''' aus, so dass man damit eine oben offene Schachtel falten kann. Die Schachtel besteht dabei aus der Grundfläche '''G''' und den Seitenflächen '''S1''' bis '''S4'''. | |||
::a.) Berechne '''x''' in Abhängigkeit von '''a''' und '''b''' für den Fall, dass das Schachtelvolumen möglichst groß ist. | |||
::b.) Was ergibt sich im Sonderfall '''a''' <math>=</math> '''b'''? | |||
::c.) Wie groß ist das maximale Volumen für '''a''' <math>=</math> 21 und '''b''' <math>=</math> 16?|3=Arbeitsmethode}} | |||
{{Achtung|Schreibe deine Gedanken, den Rechenweg und deine Ergebnisse auf einem Blatt Papier nieder. | |||
Falls du an einer Stelle nicht weiterkommst oder du zum Schluss die Lösungen vergleichen möchtest, kannst du folgende Hinweise zu Hilfe nehmen:}} | |||
Fertige eine Skizze der Aufgabenstellung an, in welche die gegebenen und gesuchten Variablen eingezeichnet werden. Dadurch sind die Zusammenhänge leichter ersichtlich. | |||
{{Lösung versteckt|Falls du die Aufgabenstellung richtig gelesen und verstanden hast, müsste deine Skizze jetzt so aussehen: | |||
[[bild:lernpfad.jpg|left]] | |||
Wie man im Bild (links) leicht erkennen kann, wird die längere Seite der ausgeschnittenen Schachtel mit <math> (a-2 \cdot x) </math> und die kürzere mit <math> (b-2 \cdot x) </math> bezeichnet. | |||
Die folgende interaktive Skizze (unten) ist dazu gedacht, dass du die Zusammenhänge der Aufgabenvariablen besser erkennst und ein bisschen mit diesen "herumspielen" kannst. | |||
Benutze dafür den Schieberegler. Ziehst du den Reglerpunkt nach links, werden die auszuschneidenden Quadrate kleiner, nach rechts werden sie größer. Zeitgleich verändert sich rechts neben der y-Achse das Volumen der "zusammengefalteten" Schachtel, welches als grüner Graph dargestellt wird. Außerdem wird dir zu jedem Volumen der zugehörige Wert der Quadratseitenlänge in türkis auf der x-Achse abgebildet. Als konkretes Beispiel dient ein Karton mit den Maßen 14cm x 10 cm. | |||
<ggb_applet width="960" height="590" id="xkcdqumt" showResetIcon="true" /> | |||
Für welches '''x''' bastelt man die Schachtel mit dem größten Volumen? | |||
Versuche es durch Ausprobieren und Ablesen!}} | |||
'''Lösungsweg zu Teilaufgabe a.)''' | |||
Nun gilt es, mit Hilfe der Variablen in der Skizze die Formel für das Schachtel-Volumen aufzustellen. Weißt du noch, wie man das Volumen eines Quaders berechnet? | |||
{{Lösung versteckt|Wie du dich vielleicht erinnerst, berechnet man das Volumen eines Quaders mit dem Merksatz "Länge mal Breite mal Höhe". Hier in unserem Fall lautet die Formel also: | |||
<math> \begin{matrix} V(x) &=& (a-2x) \cdot (b-2x) \cdot x \\ \ &=&(ab-2ax-2bx+4x^2) \cdot x \\ \ &=&4x^3-2ax^2-2bx^2+abx \end{matrix} </math> | |||
}} | |||
Jetzt bilden wir die erste Ableitung der Volumenformel '''V(x)''' und setzen diese gleich Null, um "Kandidaten" für Extrempunkte zu bekommen. | |||
{{Lösung versteckt|<math> \begin{matrix} V^\prime(x) &=&12x^2-4ax-4bx+ab \\ \ &=&12x^2-4(a+b)x+ab \end{matrix} \qquad \qquad \stackrel{!}{=} \ 0 </math> | |||
Mit Hilfe der "Mitternachtsformel" erhalten wir maximal 2 mögliche Extremstellen (da dies ein Polynom zweiten Grades ist): | |||
<math> \begin{matrix} x_{1,2} &=&\frac {4(a+b)\pm \sqrt{16(a+b)^2-4 \cdot 12 \cdot ab}}{24} \\ \ &=&\frac{4a+4b \pm \sqrt{16a^2+32ab+16b^2-48ab}}{24} \\ \ &=&\frac{4a+4b \pm \sqrt{16a^2-16ab+16b^2}}{24} \\ \ &=&\frac{4a+4b \pm 4\sqrt{a^2-ab+b^2}}{24} \\ \ &=&\frac{a+b \pm \sqrt{a^2-ab+b^2}}{6}\end{matrix} </math> | |||
:<math> \Rightarrow \qquad x_1 =\frac{a+b+ \sqrt{a^2-ab+b^2}}{6} \quad , \quad x_2 =\frac{a+b- \sqrt{a^2-ab+b^2}}{6}</math> | |||
}} | |||
Für welchen unserer Extremstellen-"Kandidaten" das Schachtelvolumen maximal wird, sehen wir nun durch sukzessives Einsetzen der erhaltenen Punkte in die zweite Ableitung der Volumenformel '''V(x)'''. | |||
{{Lösung versteckt|<math> {V^\prime}^\prime (x) = 24x-4a-4b </math> | |||
:<math> \Rightarrow </math> | |||
:::<math> {V^\prime}^\prime (x_1) = 4(a+b+ \sqrt{a^2-ab+b^2})-4a-4b =4 \sqrt{a^2-ab+b^2} \qquad > \ 0 \qquad \Rightarrow \quad x_1 \ ist \ Minimum </math> | |||
:::<math> {V^\prime}^\prime (x_2) = 4(a+b- \sqrt{a^2-ab+b^2})-4a-4b =-4 \sqrt{a^2-ab+b^2} \quad < \ 0 \qquad \Rightarrow \quad x_2 \ ist \ Maximum </math> | |||
'''Ergebnis:''' Nach Herausschneiden von Quadraten der Seitenlänge '''<math>x_2</math>''' an den Ecken des Kartons besitzt die gefaltete Schachtel das größtmögliche Volumen! | |||
}} | |||
'''Lösungsweg zu Teilaufgabe b.)''' | |||
Für den Sonderfall '''<math> a = b </math>''' ersetzen wir also nun die Variable '''b''' durch die Variable '''a''', was bedeutet, dass unser Karton jetzt quadratisch ist. Dadurch erhalten wir sofort zwei neue Lösungen für die Seitenlänge '''x''' der herauszuschneidenden Quadrate. | |||
{{Lösung versteckt|<math> x_{1,2} = \frac{2a \pm \sqrt{a^2-a^2+a^2}}{6} = \frac{2a \pm a}{6} </math> | |||
:<math> \Rightarrow </math> | |||
:::<math> x_1 = \frac{a}{2} \quad \Rightarrow \quad Fuer \ diesen \ Fall \ gibt \ es \ keine \ Schachtel, \ da \ (a-2x_1)=0 </math> | |||
:::<math> x_2 = \frac{a}{6} \quad \Rightarrow \quad {V^\prime}^\prime (x_2) = 24 \left( \frac{a}{6} \right) -4a-4a = -4a \quad < \ 0 \qquad \Rightarrow \quad x_2 \ ist \ Maximum </math> | |||
'''Ergebnis:''' Die Schachtel hat die Kanten '''a/6''', '''4a/6''' und '''4a/6'''. Das ist das Verhältnis '''<math> 1 \ : \ 4 \ : \ 4 </math>'''. | |||
}} | |||
'''Lösungsweg zu Teilaufgabe c.)''' | |||
Zum Schluß haben wir noch zwei konkrete Werte für unsere Kartonseitenlängen gegeben, nämlich '''<math> a = 21 </math>''' und '''<math> b = 16 </math>'''. Wie groß ist hierfür das maximale Volumen '''<math>V_\mathrm{max} (x) </math>'''? | |||
{{Lösung versteckt|Dazu setzen wir zunächst '''a''' und '''b''' in die Formel unseres Maximums aus Teilaufgabe a.) ein: | |||
<math>x = \frac{a+b- \sqrt{a^2-ab+b^2}}{6} = \frac{37- \sqrt{441-336+256}}{6} = \frac{37-19}{6} = 3 </math> | |||
Jetzt wissen wir, welche Länge die Quadrate haben, die wir an den Ecken des Kartons ausschneiden müssen. Mit diesem Wert lässt sich schließlich '''<math>V_\mathrm{max} (x) </math>''' berechnen: | |||
<math> V_\mathrm{max} (x) = (21-6) \cdot (16-6) \cdot 3 = 15 \cdot 10 \cdot 3 = 450 </math>. | |||
'''Skizze zur Veranschaulichung:''' | |||
Dies | Dies ist ein interaktives Koordinatensystem, in dem man durch Einstellen der Kartonseitenlängen '''a''' und '''b''' das Volumen der Schachtel durch die Funktion '''f''' in Abhängigkeit von '''x''' angezeigt bekommt. Auf der x-Achse ist die Seitenlänge der auszuschneidenden Quadrate und auf der y-Achse das Schachtelvolumen angegeben. | ||
<math> x | Vorgehensweise: Mit Hilfe der Schieberegler stellt man die gewünschten Seitenlängen des Kartons ein. Dadurch verändert sich der Graph der Funktion '''f'''. Im höchsten Punkt der nach unten geöffneten Parabel ist dann das maximale Volumen der erzeugten Schachtel angegeben. Senkrecht unterhalb dieses Punktes auf der x-Achse lässt sich dann leicht der Wert '''x''' ablesen, für den das maximale Schachtelvolumen erreicht wird. Die zweite Nullstelle des Graphen neben der Nullstelle '''<math> x = 0 </math>''' zeigt an, ab welcher Größe der auszuschneidenden Quadrate keine Schachtel mehr gefaltet werden kann. Der restliche Verlauf des Graphen ab der zweiten Nullstelle ist irrelevant. | ||
Hier fehlt noch ein Geogebra-Applet | |||
<ggb_applet width="400" height="300" filename="VolumenSkizze.ggb" showResetIcon="true" /> | |||
}} | }} | ||
===Der schräge Wurf=== | |||
{{Box|1=Aufgabe 3|2= | |||
Nun wollen wir untersuchen, in welchem Winkel du einen Ball nach vorne oben werfen musst, um eine möglichst große Wurfweite zu erzielen und welche maximale Höhe der Ball dabei jeweils erreicht.|3=Arbeitsmethode}} | |||
'''1. Skizze:''' | |||
Als erstes solltest du eine Skizze von einem Wurf nach schräg oben anfertigen. Wo befindet sich dabei der entscheidende Winkel <math>\alpha</math>? Was sind die entscheidenden Größen? | |||
''Falls du nicht weiterkommst, findest du hier die Skizze des Wurfes:'' | |||
{{Lösung versteckt|Skizze: | {{Lösung versteckt|Skizze: | ||
<ggb_applet width="400" height="250" | <ggb_applet width="400" height="250" id="nnwqsbbt" showResetIcon="true" /> | ||
}} | Als feste Größe ist die Abwurfgeschwindigkeit <math>\vec v_{0}</math> anzusehen. Dies ist die Geschwindigkeit, die du durch deine Wurfbewegung dem Ball in einer bestimmten Richtung mitgibst. Der entscheidende Parameter ist der Winkel <math>\alpha</math>.}} | ||
Entscheidend ist nun die Zerlegung der Bewegung in eine x- und eine y-Komponente. Versuche zunächst, die Geschwindigkeit an Hand der Skizze in diese Komponenten zu zerlegen. | |||
{{Lösung versteckt | {{Lösung versteckt|Die Größen <math> v_{x} </math> und <math> v_{y} </math> lassen sichmit Hilfe von <math>\alpha</math> wie folgt bestimmen: | ||
<math> v_{x}=v_{0} \cdot cos(\alpha) </math> und | <math> v_{x}=v_{0} \cdot cos(\alpha) </math> und | ||
| Zeile 88: | Zeile 335: | ||
}} | }} | ||
'''2. Physikalische Formeln''' | |||
Wir wollen allerdings die Flugweite und Flughöhe, nicht die jeweiligen Geschwindigkeiten betrachten. Erinnerst du dich, wie die Ortskomponenten in der Physik mit den Geschwindigkeitskomponenten zusammenhängen? Schreibe die entsprechenden Gleichungen auf! | |||
{{Lösung versteckt | {{Lösung versteckt|Der Ort des Wurfobjekts ergibt sich aus dem Anfangsort, der Geschwindikeit in die jeweilige Richtung mal die entsprechende Zeit und die Geschwindigkeitsänderungen (welche über die Beschleunigung ausgedrückt werden) mal die quadratische Zeit: | ||
<math> x(t)=v_{ | <math> x(t)=x_{0}+v_{0} \cdot t + \frac{1}{2} \cdot a_{0} \cdot t^2 </math> | ||
Dies müssen wir nun in x- und y-Richtung ausdrücken. In x-Richtung bleibt die Geschwindigkeit (wenn wir die Reibung vernachlässigen) über die ganze Strecke konstant und wir starten am Anfangspunkt 0: | |||
<math> x(t)=v_{x} \cdot t = v_{0} \cdot cos(\alpha) \cdot t</math> | |||
In y-Richtung starten wir ebenfalls am Anfangspunkt 0, allerdings nimmt die Geschwindigkeit mit der Erdbeschleunigung g ab: | |||
<math> y(t)=v_{y} \cdot t - 1/2 \cdot g \cdot t^2 = v_{0} \cdot sin(\alpha) \cdot t - 1/2 \cdot g \cdot t^2</math> | |||
}} | }} | ||
'''3. Nebenbedingung formulieren''' | |||
Nun musst du dir klar werden, welche Größen du darstellen willst! In unserem Fall: Wurfweite x in Abhängigkeit des Wurfwinkels <math> \alpha </math>. Steht dies schon da? Oder steht in der Funktion eine Variable, die stört bzw. nicht gegeben ist? Dann musst du diese Variable durch deine eigentlich interessanten Größen ausdrücken, oder anders gesagt, eine Nebenbedinung formulieren. | Nun musst du dir klar werden, welche Größen du darstellen willst! In unserem Fall: Wurfweite x in Abhängigkeit des Wurfwinkels <math> \alpha </math>. Steht dies schon da? Oder steht in der Funktion eine Variable, die stört bzw. nicht gegeben ist? Dann musst du diese Variable durch deine eigentlich interessanten Größen ausdrücken, oder anders gesagt, eine Nebenbedinung formulieren. | ||
Tipp: Nicht erschrecken vor zunächst etwas unhandlichen Termen. | |||
''Tipp: Nicht erschrecken vor zunächst etwas unhandlichen Termen.'' | |||
Falls du nicht weiterkommst, findest du hier die Nebenbedingung mit entsprechender Auflösung: | Falls du nicht weiterkommst, findest du hier die Nebenbedingung mit entsprechender Auflösung: | ||
{{Lösung versteckt | |||
{{Lösung versteckt|Störend ist bei uns noch die Variable t. Wir interessieren uns ja nur für den Zeitpunkt, an dem der Ball/Stein oder ähnliches wieder auf dem Boden aufkommt. Dies ist genau der Zeitpunkt, bei dem unsere zweite Ortsfunktion y(t) (also die Höhe) wieder 0 ist. Als Funktion: | |||
<math> y(x)=v_{y}(t) \cdot t - \frac{1}{2} \cdot g \cdot t^2 = v_{0}(t) \cdot sin(\alpha) \cdot t - \frac{1}{2} \cdot g \cdot t^2 =0 </math> | <math> y(x)=v_{y}(t) \cdot t - \frac{1}{2} \cdot g \cdot t^2 = v_{0}(t) \cdot sin(\alpha) \cdot t - \frac{1}{2} \cdot g \cdot t^2 =0 </math> | ||
| Zeile 123: | Zeile 383: | ||
}} | }} | ||
Wenn du die Nebenbedingung formuliert hast und umgeformt hast, kannst du die störende Variable durch für die Aufgabe | '''4. Nebenbedingung einsetzen und Funktion aufstellen''' | ||
Wenn du die Nebenbedingung formuliert hast und umgeformt hast, kannst du die störende Variable durch die für die Aufgabe wesentlichen Größen ausdrücken und in die Zielfunktion einsetzen. | |||
{{Lösung versteckt | {{Lösung versteckt| | ||
Mit der Information über t können wir t nun in unserer Ortsfunktion <math> x(t,\alpha) </math> elimieren. | |||
<math> x(t_{2},\alpha)= v_{0} \cdot cos(\alpha) \cdot t_{2} = v_{0} \cdot cos(\alpha) \cdot \frac{2 \cdot v_{0} \cdot sin(\alpha)}{g}= \frac {2 \cdot v_{0}^2}{g} \cdot cos(\alpha) \cdot sin(\alpha)=x(\alpha) </math> | <math> x(t_{2},\alpha)= v_{0} \cdot cos(\alpha) \cdot t_{2} = v_{0} \cdot cos(\alpha) \cdot \frac{2 \cdot v_{0} \cdot sin(\alpha)}{g}= \frac {2 \cdot v_{0}^2}{g} \cdot cos(\alpha) \cdot sin(\alpha)=x(\alpha) </math> | ||
Somit hängt unsere Wurfweite wie gewollt nur noch vom Abwurfwinkel <math> \alpha </math> ab. | Somit hängt unsere Wurfweite wie gewollt nur noch vom Abwurfwinkel <math> \alpha </math> ab. In der Skizze kannst du zusätzlich die Abwurfgeschwindigkeit <math> v_{0} </math> variieren, die wir in der Berechnung zunächst einmal als fest voraussetzen. | ||
Skizze: | Skizze: | ||
<ggb_applet width="400" height="250" | <ggb_applet width="400" height="250" id="tgvxwrcu" showResetIcon="true" />}} | ||
'''5. Bestimmung des Extremwerts (maximale Wurfweite)''' | |||
Du hast nun eine Funktion, die dir die Wurfweite in Abhängigkeit des Winkels darstellt. Wir wollen den Winkel herausfinden, bei dem die Wurfweite maximal wird. Wir suchen also das Maximum von <math> x(\alpha)</math>. | |||
Dieses Maximum können wir bestimmen, indem wir die Funktion einmal ableiten und die Nullstellen dieser Ableitung suchen. Da die Funktion nur von <math> \alpha </math> abhängt, musst du jetzt natürlich nach <math> \alpha </math> ableiten. Versuche, die Nullstelle zu bestimmen. | |||
{{Lösung versteckt|Die Funktion | |||
= | <math> x(\alpha) = \frac {2 \cdot v_{0}^2}{g} \cdot cos(\alpha) \cdot sin(\alpha) </math> soll maximiert werden. | ||
Erste Ableitung: | |||
{{ | <math> x'(\alpha)= \frac{2 \cdot v_{0}^2}{g} (-sin(\alpha) \cdot sin(\alpha)+cos(\alpha)cos(\alpha))\qquad \qquad (Produktregel) </math> | ||
( | <math> x'(\alpha) = \frac{2 \cdot v_{0}^2}{g} (cos(\alpha)^2 - sin(\alpha)^2) </math> | ||
( | <math> x'(\alpha) = \frac{2 \cdot v_{0}^2}{g} (1-2sin(\alpha)^2) \stackrel{!}{=} 0 \qquad \qquad (sin(x)^2+cos(x)^2=1)</math> | ||
<math> \Leftrightarrow 2 \cdot sin(\alpha)^2 = 1 \qquad \Leftrightarrow sin(\alpha) = \pm \frac{1}{\sqrt{2}} </math> | |||
<math> \Leftrightarrow \qquad \alpha = \pm 45^\circ </math> | |||
Die negative Lösung entspräche dem Abwurf in 45° nach unten in den Boden, also eine nichtpraktische Lösung. | |||
<math> \Rightarrow \qquad \alpha = 45^\circ </math> | |||
Zur Überprüfung, ob es sich tatsächlich um ein Maximum handelt, sollten wir noch die 2. Ableitung überprüfen: | |||
<math> x''(\alpha) = - \frac{8 \cdot sin(\alpha) \cdot cos(\alpha)}{g} < 0 \qquad \qquad \alpha \approx 45^\circ </math> | |||
Somit handelt es sich tatsächlich um ein Maximum und die Wurfweite wird bei <math> \alpha = 45^\circ </math> maximal. | |||
}} | |||
'''6. Untersuchung der Flughöhe''' | |||
Du hast nun herausgefunden, dass die Flugweite eines geworfenen Objekts nicht nur von der Anfangsgeschwindigkeit abhängt, sondern auch vom Winkel, in dem das Objekt abgeworfen wird. Unter dem soeben bestimmten Winkel ist die Flugweite maximal. | |||
Versuche nun noch zu berechnen, welche maximale Höhe das Objekt dabei erreicht. Wir suchen also wieder den Extremwert, diesmal allerdings den maximalen Wert der Höhe. Die Höhe wurde bisher als Funktion y(t) bezeichnet. Klar ist, dass der Ball wohl je höher fliegen wird, je steiler man ihn nach oben wirft und die Flughöhe bei <math> \alpha=0^\circ </math>, also den Wurf senkrecht nach oben, sein Maximum haben wird. | |||
Die Frage ist nun allerdings wie hoch der Ball unter dem berechneten "optimalen" Abwurfwinkel fliegt. | |||
{{Lösung versteckt|Wir müssen die Ableitung der Funktion y(t) wieder gleich 0 setzen, um die Extremwerte der Funktion herauszufinden und diese Werte dann mithilfe der 2. Ableitung überprüfen: | |||
<math> y(t)= v_{0} \cdot sin(\alpha) \cdot t - \frac{1}{2} \cdot g \cdot t^2 </math> | |||
' | <math> y'(t)= v_{0} \cdot sin(\alpha) - \frac{1}{2} \cdot g \cdot 2 \cdot t \stackrel{!}{=} 0</math> | ||
<math> \Rightarrow t_{max} = \frac{ v_{0} \cdot sin(\alpha)}{g} </math> | |||
Einsetzen in y(t): | |||
<math> y(t_{max})= v_{0} \cdot sin(\alpha) \frac{v_{0} \cdot sin(\alpha)}{g} - \frac{1}{2} \cdot g \frac{v_{0}^2 \cdot sin(\alpha)^2}{g^2} </math> | |||
<math> = \frac{v_{0}^2 \cdot sin(\alpha)^2}{g} - \frac{v_{0}^2 \cdot sin(\alpha)^2}{2g} </math> | |||
<math> = \frac{v_{0}^2 \cdot sin(\alpha)^2}{2g} </math> | |||
Einsetzen von <math> \alpha_{max}=45^\circ </math> | |||
<math> y(t_{max})= \frac{v_{0}^2}{4g} </math> | |||
Zuletzt noch die Überprüfun der 2. Ableitung: | |||
<math> y''(t_{max})= -g < 0 </math> | |||
Somit handelt es sich um ein Maximum und wir haben die Flughöhe für beliebige Anfangsgeschwindigkeiten bestimmt. | |||
}} | |||
Herzlichen Glückwunsch! Du hast das Extremwertproblem des schrägen Wurfes gelöst! | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Sekundarstufe 2]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie: | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Analysis]] | |||
Aktuelle Version vom 24. April 2022, 10:00 Uhr
Einführung
Willkommen zum Lernpfad "Anwendungsbezogene Extremwertaufgaben". Hier findet ihr Aufgaben, in denen die Bestimmung von Extremwerten anhand von Beispielen aus dem Alltag eingeübt und vertieft werden kann.
Kurz zur Wiederholung:
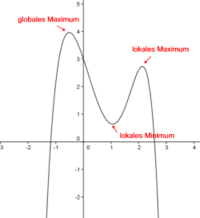
Ein Extremwert ist der größte bzw. kleinste Wert einer Funktion (in einem gewissen Bereich). Hier kannst du dir nochmal die formale Definition eines Extremwerts einblenden.
Es sei eine Teilmenge der Reellen Zahlen (z.B. ein Intervall) und eine Funktion.
f hat an der Stelle
- ein lokales Minimum, wenn es ein Intervall gibt, das enthält, so dass für alle gilt;
- ein globales Minimum, wenn für alle gilt;
- ein lokales Maximum, wenn es ein Intervall gibt, das enthält, so dass für alle gilt;
- ein globales Maximum, wenn für alle gilt.
Um diesen Wert zu finden, ist es sinnvoll die Ableitung der Funktion näher zu betrachten. Diese beschreibt nämlich anschaulich die Steigung einer angelegten Tangente an der ursprünglichen Funktion. Bei einem Extremwert, ist diese Tangente waagrecht, d.h. die Ableitungsfunktion an dieser Stelle ist Null.
Diesen Sachverhalt kannst du dir nochmal in folgender Skizze näher anschauen:

Du siehst hier die Funktion , an der du die Werte a, b, c und d verändern kannst. Wie du siehst, gibt es an bestimmten Stellen maximale und minimale Werte. Betrachte nun folgende Aspekte:
- Welchen Einfluss haben die Parameter a, b, c und d auf die Funktion? Wo liegen die Unterschiede?
- Wo befinden sich die Maxima und Minima der Funktion
- Blende die Ableitungsfunktion ein. Welchen Zusammenhang siehst du? Wie ändert sich die Ableitung mit der Veränderung von a, b, c und d? Was erkennst du bei der Änderung von d?
- Um den Zusammenhang deutlicher zu sehen, klicke auf das Kontrollkästchen Extremwerte
Wozu überhaupt Extremwerte?
Extremwerte geben maximale bzw. minimale Größen bei vorgegebenen Randbedingungen an und sind Lösungen bei sogenannten Optimierungsproblemen, d.h. sie geben den idealen Zusammenhang der Funktionsgrößen wieder. Im folgenden soll dies an drei Beispielen verdeutlicht werden. Als erstes wollen wir untersuchen, auf welchem Weg ein Ziel am schnellsten erreicht werden kann (dies ist nicht immer der direkteste Weg). Danach schauen wir uns an, wie man eine größtmögliche Schachtel aus vorgegebenen Karton basteln kann. Als letztes soll untersucht werden, in welchem Winkel man einen Ball werfen muss, um damit eine maximale Wurfweite zu erzielen.
Dies ist ein Ausschnitt aus einem breiten Anwendungsbereich von Extremwertaufgaben bzw. der Differentialrechnung. Denn auch in der Natur werden meist Zustände angenommen, die minimale Energie benötigen und somit über Extremwertbestimmungen ermittelt werden könne.
Nun aber zu unseren Aufgaben...
Beispiele für anwendungsbezogene Extremwertaufgaben (mit Lösungsanleitung)
Extremwertaufgabe mit Nebenbedingung: Der schnellste Weg
Ein Acker liegt an einer geradlinigen Straße. Ein Fußgänger befindet sich auf dem Acker im Punkt A und möchte möglichst schnell zu einem Punkt B auf der Straße gelangen. Der Fußpunkt C des Lotes von A auf die Straße hat von A die Entfernung 400m und die Entfernung B nach C betrage
(a.) 1000m
(b.) 100m.
Auf der Straße kann sich der Fußgänger doppelt so schnell fortbewegen wie auf dem Acker. Welchen Weg soll er einschlagen?
Hilfestellung:
1. Stelle die Aufgabensituation in einer Skizze dar (Teilaufgabe a)):
Beschrifte, was gegeben und gesucht ist. Gebe den Bekannten und Unbekannten passende Namen.
Hier kannst die die Aufgabensituation in einer Skizze betrachten (links der y-Achse im Koordinatensystem) und nebenstehend den Graphen der zu minimierenden Funktion f in der Variablen d (rechts der y-Achse im Koordinatensystem). Diese Funktion f musst du nachher noch bestimmen.
Indem du den Punkt D verschiebst, ändert sich d und somit auch der Funktionswert f(d), was zu dem rechten Graphen führt (grüne Spur).
Bevor wir zur Extremwertberechnung kommen, hier einige Vorüberlegungen:
- Verschiebe den Punkt D und betrachte den nebenstehenden Graphen (grün)!
- Bei welchem Wert d wird der Funktionswert von f minimal? Lese den Wert näherungsweise an der x-Achse bzw. an der Anzeige der Streckenlänge d ab.
- Wie groß sind jeweils die Streckenlängen auf dem Acker a (braune Linie)und der Straße (rote Linie)? Wie kann man diese berechnen?
Notiere deine Gedanken und überprüfe später diese Werte durch die genaue Berechnung des Extremwertes und somit der Streckenlängen, die auf dem Acker und der Straße zurückgelegt werden müssen.

2. Zielfunktion für Teilaufgabe a) :
Erkenne die Zielfunktion und formuliere sie als mathematische Funktion in Abhängigkeit von den Ausgangsgrößen und Unbekannten.
Der Weg des Fußgängers setzt sich aus 2 Teilstrecken zusammen, nämlich aus einem geraden Weg über den Acker von A nach D (D liegt auf der Straße), also Strecke a (braune Linie), und dem Teilstück b (rote Linie) von D nach B auf der Straße.
- Sei d der Abstand von C (Fußpunkt des Lotes durch A auf die Straße) und D, wobei .
- Die Länge des Weges von D nach C, also die rote Strecke b, ist 1000 - d.
- Da der Fußgänger auf dem Acker nur halb so schnell voran kommt wie auf der Straße, müssen die dort zurückzulegenden Meter doppelt gezählt werden.
Die Überlegungen führen uns zu folgender Zielfunktion:
Diese ist zu minimieren.
3. Nebenbedingung in Zielfunktion für Teilaufgabe a):
Erkenne die Nebenbedingung, die unabhängige Größen der Zielfunktion zueinander in Beziehung setzt, formuliere sie als mathematischen Ausdruck und setze sie in die Zielfunktion so ein, dass eine äquivalente Zielfunktion für den zu optimierenden Wert in Abhängigkeit von nur einer Variablen entsteht.
Die Länge des Weges a von A nach D ist nach Pythagoras .
Mit dieser Nebenbedingung ergibt sich durch Ersetzen von a in der Zielfunktion:
4. Bestimmung des Extremwertes der Zielfunktion für Teilaufgabe a) und b):
Bestimmung des Extremwertes durch Nullsetzen der ersten Ableitung und Überprüfung des Vorzeichens der zweiten Ableitung.
Teilaufgabe a)
- Um den Extremwert der Zielfunktion bzw. den schnellsten Weg, um von A nach B zu kommen, zu bestimmen, benötigen wir die erste Ableitung dieser Funktion, die wir gleich 0 setzen, also :
- Durch Auflösen dieser Bedingung nach d erhält man als Lösung
- Um nachzuprüfen, ob an dieser Stelle ein lokales Minimum (schnellster Weg) vorliegt, berechnen wir die zweite Ableitung der Zielfunktion f''(d) und prüfen, ob durch Einsetzen von unserer Lösung in f''(d) eine Zahl größer als 0 vorliegt, also ob f''(d)>0:
Es gilt
und somit
- Die Weglänge über die Straße, also die Entfernung von Punkt D zu B, beträgt also
.
Die Weglänge über den Acker beträgt
.
Teilaufgabe b)
- Wenn allerdings der Abstand zwischen B und C nur 100m beträgt, so lautet die zu minimierende Zielfunktion
- Die Ableitung hiervon ist die gleiche wie in Teilaufgabe a) schon betrachtet:
.
Setzt man diese Ableitung gleich 0, so hat sie für keine Nullstelle bzw. keine Lösung. Hiermit gibt es in diesem Fall kein lokales Minimum. Die Funktion ist im Intervall [0,100] also streng monoton, weshalb der minimale Wert am Rand des Definitionsbereiches liegen muss, also entweder bei oder bei .
- Durch Einsetzen von d = 0 erhält man
Durch Einsetzen von d = 100 erhält man
Da der Funktionswert für d=100 der kleinere ist, führt folglich der kürzeste Weg von A nach B auf gerader Linie direkt über den Acker.Bastelstunde: Falten einer Schachtel
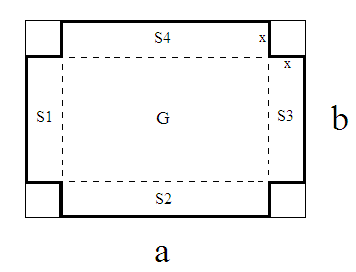
Von einem rechteckigen Karton mit Seitenlängen a und b (mit b a) schneidet man an den Ecken Quadrate der Seitenlänge x aus, so dass man damit eine oben offene Schachtel falten kann. Die Schachtel besteht dabei aus der Grundfläche G und den Seitenflächen S1 bis S4.
- a.) Berechne x in Abhängigkeit von a und b für den Fall, dass das Schachtelvolumen möglichst groß ist.
- b.) Was ergibt sich im Sonderfall a b?
- c.) Wie groß ist das maximale Volumen für a 21 und b 16?
Schreibe deine Gedanken, den Rechenweg und deine Ergebnisse auf einem Blatt Papier nieder.
Falls du an einer Stelle nicht weiterkommst oder du zum Schluss die Lösungen vergleichen möchtest, kannst du folgende Hinweise zu Hilfe nehmen:
Fertige eine Skizze der Aufgabenstellung an, in welche die gegebenen und gesuchten Variablen eingezeichnet werden. Dadurch sind die Zusammenhänge leichter ersichtlich.
Falls du die Aufgabenstellung richtig gelesen und verstanden hast, müsste deine Skizze jetzt so aussehen:
Wie man im Bild (links) leicht erkennen kann, wird die längere Seite der ausgeschnittenen Schachtel mit und die kürzere mit bezeichnet.
Die folgende interaktive Skizze (unten) ist dazu gedacht, dass du die Zusammenhänge der Aufgabenvariablen besser erkennst und ein bisschen mit diesen "herumspielen" kannst.
Benutze dafür den Schieberegler. Ziehst du den Reglerpunkt nach links, werden die auszuschneidenden Quadrate kleiner, nach rechts werden sie größer. Zeitgleich verändert sich rechts neben der y-Achse das Volumen der "zusammengefalteten" Schachtel, welches als grüner Graph dargestellt wird. Außerdem wird dir zu jedem Volumen der zugehörige Wert der Quadratseitenlänge in türkis auf der x-Achse abgebildet. Als konkretes Beispiel dient ein Karton mit den Maßen 14cm x 10 cm.

Für welches x bastelt man die Schachtel mit dem größten Volumen?
Versuche es durch Ausprobieren und Ablesen!
Lösungsweg zu Teilaufgabe a.)
Nun gilt es, mit Hilfe der Variablen in der Skizze die Formel für das Schachtel-Volumen aufzustellen. Weißt du noch, wie man das Volumen eines Quaders berechnet?
Wie du dich vielleicht erinnerst, berechnet man das Volumen eines Quaders mit dem Merksatz "Länge mal Breite mal Höhe". Hier in unserem Fall lautet die Formel also:
Jetzt bilden wir die erste Ableitung der Volumenformel V(x) und setzen diese gleich Null, um "Kandidaten" für Extrempunkte zu bekommen.
Mit Hilfe der "Mitternachtsformel" erhalten wir maximal 2 mögliche Extremstellen (da dies ein Polynom zweiten Grades ist):
Für welchen unserer Extremstellen-"Kandidaten" das Schachtelvolumen maximal wird, sehen wir nun durch sukzessives Einsetzen der erhaltenen Punkte in die zweite Ableitung der Volumenformel V(x).
Ergebnis: Nach Herausschneiden von Quadraten der Seitenlänge an den Ecken des Kartons besitzt die gefaltete Schachtel das größtmögliche Volumen!
Lösungsweg zu Teilaufgabe b.)
Für den Sonderfall ersetzen wir also nun die Variable b durch die Variable a, was bedeutet, dass unser Karton jetzt quadratisch ist. Dadurch erhalten wir sofort zwei neue Lösungen für die Seitenlänge x der herauszuschneidenden Quadrate.
Ergebnis: Die Schachtel hat die Kanten a/6, 4a/6 und 4a/6. Das ist das Verhältnis .
Lösungsweg zu Teilaufgabe c.)
Zum Schluß haben wir noch zwei konkrete Werte für unsere Kartonseitenlängen gegeben, nämlich und . Wie groß ist hierfür das maximale Volumen ?
Dazu setzen wir zunächst a und b in die Formel unseres Maximums aus Teilaufgabe a.) ein:
Jetzt wissen wir, welche Länge die Quadrate haben, die wir an den Ecken des Kartons ausschneiden müssen. Mit diesem Wert lässt sich schließlich berechnen:
.
Skizze zur Veranschaulichung:
Dies ist ein interaktives Koordinatensystem, in dem man durch Einstellen der Kartonseitenlängen a und b das Volumen der Schachtel durch die Funktion f in Abhängigkeit von x angezeigt bekommt. Auf der x-Achse ist die Seitenlänge der auszuschneidenden Quadrate und auf der y-Achse das Schachtelvolumen angegeben.
Vorgehensweise: Mit Hilfe der Schieberegler stellt man die gewünschten Seitenlängen des Kartons ein. Dadurch verändert sich der Graph der Funktion f. Im höchsten Punkt der nach unten geöffneten Parabel ist dann das maximale Volumen der erzeugten Schachtel angegeben. Senkrecht unterhalb dieses Punktes auf der x-Achse lässt sich dann leicht der Wert x ablesen, für den das maximale Schachtelvolumen erreicht wird. Die zweite Nullstelle des Graphen neben der Nullstelle zeigt an, ab welcher Größe der auszuschneidenden Quadrate keine Schachtel mehr gefaltet werden kann. Der restliche Verlauf des Graphen ab der zweiten Nullstelle ist irrelevant.
Hier fehlt noch ein Geogebra-Applet

Der schräge Wurf
1. Skizze:
Als erstes solltest du eine Skizze von einem Wurf nach schräg oben anfertigen. Wo befindet sich dabei der entscheidende Winkel ? Was sind die entscheidenden Größen?
Falls du nicht weiterkommst, findest du hier die Skizze des Wurfes:
Skizze:

Entscheidend ist nun die Zerlegung der Bewegung in eine x- und eine y-Komponente. Versuche zunächst, die Geschwindigkeit an Hand der Skizze in diese Komponenten zu zerlegen.
Die Größen und lassen sichmit Hilfe von wie folgt bestimmen:
und
2. Physikalische Formeln
Wir wollen allerdings die Flugweite und Flughöhe, nicht die jeweiligen Geschwindigkeiten betrachten. Erinnerst du dich, wie die Ortskomponenten in der Physik mit den Geschwindigkeitskomponenten zusammenhängen? Schreibe die entsprechenden Gleichungen auf!
Der Ort des Wurfobjekts ergibt sich aus dem Anfangsort, der Geschwindikeit in die jeweilige Richtung mal die entsprechende Zeit und die Geschwindigkeitsänderungen (welche über die Beschleunigung ausgedrückt werden) mal die quadratische Zeit:
Dies müssen wir nun in x- und y-Richtung ausdrücken. In x-Richtung bleibt die Geschwindigkeit (wenn wir die Reibung vernachlässigen) über die ganze Strecke konstant und wir starten am Anfangspunkt 0:
In y-Richtung starten wir ebenfalls am Anfangspunkt 0, allerdings nimmt die Geschwindigkeit mit der Erdbeschleunigung g ab:
3. Nebenbedingung formulieren
Nun musst du dir klar werden, welche Größen du darstellen willst! In unserem Fall: Wurfweite x in Abhängigkeit des Wurfwinkels . Steht dies schon da? Oder steht in der Funktion eine Variable, die stört bzw. nicht gegeben ist? Dann musst du diese Variable durch deine eigentlich interessanten Größen ausdrücken, oder anders gesagt, eine Nebenbedinung formulieren.
Tipp: Nicht erschrecken vor zunächst etwas unhandlichen Termen.
Falls du nicht weiterkommst, findest du hier die Nebenbedingung mit entsprechender Auflösung:
Störend ist bei uns noch die Variable t. Wir interessieren uns ja nur für den Zeitpunkt, an dem der Ball/Stein oder ähnliches wieder auf dem Boden aufkommt. Dies ist genau der Zeitpunkt, bei dem unsere zweite Ortsfunktion y(t) (also die Höhe) wieder 0 ist. Als Funktion:
um t zu elimieren, müssen wir diese Gleichung nach t auflösen. Etwas anders sortiert lässt sich die Gleichung auch schreiben als
Dies ist eine einfache quadratische Gleichung, die sich mit der Mitternachtsformel lösen lässt:
Wir erinnern uns, dass und jeweils die Zeiten sind, an denen die Höhe des Wurfobjekts 0 ist. Dies ist logischerweise zur Zeit 0 der Fall, was unserer Lösung entspricht. Die für uns interessante Lösung ist allerdings , also die Zeit, wenn das Wurfobjekt nach dem Wurf wieder am Boden ist.
4. Nebenbedingung einsetzen und Funktion aufstellen
Wenn du die Nebenbedingung formuliert hast und umgeformt hast, kannst du die störende Variable durch die für die Aufgabe wesentlichen Größen ausdrücken und in die Zielfunktion einsetzen.
Mit der Information über t können wir t nun in unserer Ortsfunktion elimieren.
Somit hängt unsere Wurfweite wie gewollt nur noch vom Abwurfwinkel ab. In der Skizze kannst du zusätzlich die Abwurfgeschwindigkeit variieren, die wir in der Berechnung zunächst einmal als fest voraussetzen.
Skizze:

5. Bestimmung des Extremwerts (maximale Wurfweite)
Du hast nun eine Funktion, die dir die Wurfweite in Abhängigkeit des Winkels darstellt. Wir wollen den Winkel herausfinden, bei dem die Wurfweite maximal wird. Wir suchen also das Maximum von .
Dieses Maximum können wir bestimmen, indem wir die Funktion einmal ableiten und die Nullstellen dieser Ableitung suchen. Da die Funktion nur von abhängt, musst du jetzt natürlich nach ableiten. Versuche, die Nullstelle zu bestimmen.
Die Funktion
soll maximiert werden.
Erste Ableitung:
Die negative Lösung entspräche dem Abwurf in 45° nach unten in den Boden, also eine nichtpraktische Lösung.
Zur Überprüfung, ob es sich tatsächlich um ein Maximum handelt, sollten wir noch die 2. Ableitung überprüfen:
Somit handelt es sich tatsächlich um ein Maximum und die Wurfweite wird bei maximal.
6. Untersuchung der Flughöhe
Du hast nun herausgefunden, dass die Flugweite eines geworfenen Objekts nicht nur von der Anfangsgeschwindigkeit abhängt, sondern auch vom Winkel, in dem das Objekt abgeworfen wird. Unter dem soeben bestimmten Winkel ist die Flugweite maximal.
Versuche nun noch zu berechnen, welche maximale Höhe das Objekt dabei erreicht. Wir suchen also wieder den Extremwert, diesmal allerdings den maximalen Wert der Höhe. Die Höhe wurde bisher als Funktion y(t) bezeichnet. Klar ist, dass der Ball wohl je höher fliegen wird, je steiler man ihn nach oben wirft und die Flughöhe bei , also den Wurf senkrecht nach oben, sein Maximum haben wird. Die Frage ist nun allerdings wie hoch der Ball unter dem berechneten "optimalen" Abwurfwinkel fliegt.
Wir müssen die Ableitung der Funktion y(t) wieder gleich 0 setzen, um die Extremwerte der Funktion herauszufinden und diese Werte dann mithilfe der 2. Ableitung überprüfen:
Einsetzen in y(t):
Einsetzen von
Zuletzt noch die Überprüfun der 2. Ableitung:
Somit handelt es sich um ein Maximum und wir haben die Flughöhe für beliebige Anfangsgeschwindigkeiten bestimmt.
Herzlichen Glückwunsch! Du hast das Extremwertproblem des schrägen Wurfes gelöst!