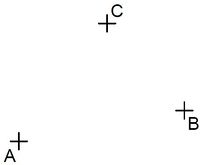Jahrgangsstufentest/BMT8 2011: Unterschied zwischen den Versionen
Main>Andrea schellmann (Lösungen ergänzt) |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[https://www.isb.bayern.de/gymnasium/leistungserhebungen/jahrgangsstufenarbeiten-gymnasium/mathematik/2011/ '''Test und Lösungshinweise zum Download'''] | |||
[ | |||
< | <div class="rahmen"> | ||
<big>'''Aufgabe 1'''</big> | |||
Lukas macht eine Mountainbike-Tour rund um den Hochfelln. Die Abbildung zeigt das Streckenprofil seiner insgesamt 35 km langen Tour, die am Parkplatz der Hochfelln-Bahn beginnt und endet. | |||
::[[Datei:BMT 8 2011 A1.jpg|600px|center]] | |||
'''a)''' An der Grabenhäuslhütte merkt Lukas, dass er zu Beginn der Tour vergessen hat, seinen | |||
Kilometerzähler auf null zurückzusetzen; er tut dies nun nachträglich. Wie wird der Zählerstand | Kilometerzähler auf null zurückzusetzen; er tut dies nun nachträglich. Wie wird der Zählerstand | ||
in Urschlau lauten? | in Urschlau lauten? | ||
{{Lösung versteckt|1= | |||
'''15 km''' | |||
}} | }} | ||
'''b)''' Nach der Tour stellt Lukas fest: „Bei der Abfahrt von der Eschelmooshütte bis zum Parkplatz habe ich pro Minute 25 Meter an Höhe verloren.“ Berechne, wie lange er für die Abfahrt gebraucht hat und mit welcher Durchschnittsgeschwindigkeit in <math>\frac{km}{h}</math> er die dabei zurückgelegte Strecke gefahren ist. | |||
{{Lösung versteckt|1= | |||
benötigte Zeit: '''500m : 25'''<math>\frac{m}{min}</math> = '''20 min''' | |||
Geschwindigkeit: '''27''' <math>\frac{km}{h}</math> | |||
}} | |||
Welchen Anteil der Höhenmeter, die Lukas insgesamt bergauf bewältigen muss, hat er an der Grabenhäuslhütte ungefähr bereits hinter sich? | <div class="multiplechoice-quiz"> | ||
'''c)''' Welchen Anteil der Höhenmeter, die Lukas insgesamt bergauf bewältigen muss, hat er an der Grabenhäuslhütte ungefähr bereits hinter sich? | |||
(!25 %) | (!25 %) | ||
| Zeile 56: | Zeile 37: | ||
</div> | </div> | ||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 2a'''</big> | <big>'''Aufgabe 2a'''</big> | ||
Betrachtet wird ein beliebiges Trapez ABCD mit AB || CD. | Betrachtet wird ein beliebiges Trapez ABCD mit AB || CD. | ||
<br><br> | |||
[[Datei:BMT 8 2011 A2.jpg|400px|center]] | |||
<br> | |||
(!γ = 90° + β) | (!γ = 90° + β) | ||
| Zeile 72: | Zeile 54: | ||
</div> | </div> | ||
<div | <div class="rahmen"> | ||
<big>'''Aufgabe 2b'''</big> | <big>'''Aufgabe 2b'''</big> | ||
An jedes Trapez ABCD lässt sich ein dazu kongruentes Trapez so anfügen, dass ein Parallelogramm entsteht (vgl. Abbildung). Gib eine Formel an, mit der man allgemein den Flächeninhalt eines Trapezes bestimmen kann. Trage alle verwendeten Benennungen in die Abbildung ein; ergänze die Abbildung geeignet. | An jedes Trapez ABCD lässt sich ein dazu kongruentes Trapez so anfügen, dass ein Parallelogramm entsteht (vgl. Abbildung). Gib eine Formel an, mit der man allgemein den Flächeninhalt eines Trapezes bestimmen kann. Trage alle verwendeten Benennungen in die Abbildung ein; ergänze die Abbildung geeignet. | ||
{{Lösung versteckt|1= | |||
Flächeninhalt eines Trapezes: <math>A_{Trapez} = \frac{1}{2}\cdot (a + c) \cdot h</math> | |||
[[Datei:BMT 8 2011 A2b.jpg|400px]] | |||
Den Flächeninhalt des Parallelogramms kann man mit der Formel <math>A_{Parallelogramm} = (a+c)\cdot h</math> berechnen (Grundlinie mal zugehörige Höhe). | |||
Da das Trapez genau die Hälfte des Parallelogramms ist, ergibt sich die oben angegebene Formel. | |||
}} | }} | ||
</div> | </div> | ||
<div | <div class="rahmen"> | ||
<big>'''Aufgabe 3'''</big> | <big>'''Aufgabe 3'''</big> | ||
In der folgenden Gleichung stehen a und b für rationale Zahlen. | In der folgenden Gleichung stehen a und b für rationale Zahlen. | ||
ax = 7x + b | |||
'''a)''' Bestimme die Lösung der Gleichung für a = 3 und b = 8 . | |||
{{Lösung versteckt|1= | |||
:3x = 7x + 8 | :3x = 7x + 8 | ||
: | : | ||
| Zeile 110: | Zeile 87: | ||
:'''x = -2''' | :'''x = -2''' | ||
}} | }} | ||
'''b)''' Gib Werte für a und b so an, dass die Gleichung die Lösung x = -5 hat. | |||
{{Lösung versteckt|1= | |||
:z.B. a = 0, b = 35 | :z.B. a = 0, b = 35 | ||
}} | }} | ||
'''c)''' Gib Werte für a und b so an, dass die Gleichung keine Lösung hat. | |||
{{Lösung versteckt|1= | |||
:z.B. a = 7, b = 1 | :z.B. a = 7, b = 1 | ||
:''a muss 7 sein, für b können alle Werte außer Null angegeben werden.'' | :''a muss 7 sein, für b können alle Werte außer Null angegeben werden.'' | ||
}} | }} | ||
</div> | </div> | ||
<div class="rahmen"> | |||
<big>'''Aufgabe 4'''</big> | |||
Marie möchte alle Punkte markieren, die von A und B den gleichen Abstand haben und gleichzeitig | Marie möchte alle Punkte markieren, die von A und B den gleichen Abstand haben und gleichzeitig | ||
von C weniger als 1,5 cm entfernt sind. Ergänze sinnvoll, was sie sich dazu überlegen könnte. | von C weniger als 1,5 cm entfernt sind. Ergänze sinnvoll, was sie sich dazu überlegen könnte. | ||
| Zeile 148: | Zeile 114: | ||
„Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf ... sowie ... .“ | „Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf ... sowie ... .“ | ||
[[Datei:BMT 8 2011 A4.jpg|200px|right]] | |||
{{Lösung versteckt|1= | |||
:Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf '''der Mittelsenkrechten der Strecke [AB]''' sowie '''im Inneren des Kreises um C mit Radius 1,5 cm'''. | :Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf '''der Mittelsenkrechten der Strecke [AB]''' sowie '''im Inneren des Kreises um C mit Radius 1,5 cm'''. | ||
}} | }} | ||
</div> | </div> | ||
<div | <div class="rahmen"> | ||
<big>'''Aufgabe 5'''</big> | <big>'''Aufgabe 5'''</big> | ||
Vereinfache jeweils so weit wie möglich. | Vereinfache jeweils so weit wie möglich. | ||
'''a)''' <math> 2a \cdot (1,5b \cdot 4a) = </math> | |||
{{Lösung versteckt|1= | |||
: <math> 2a \cdot (1,5b \cdot 4a) = 2a \cdot 1,5b \cdot 4a = </math> '''<math> 12a^2b </math>''' ''Achtung: Hier gilt kein Distributivgesetz!'' | |||
< | |||
: | |||
}} | }} | ||
'''b)''' <math> x - (\frac{3}{7} x + 5) = </math> | |||
{{Lösung versteckt|1= | |||
:<math> x - (\frac{3}{7}x + 5) = x - \frac{3}{7}x - 5 = </math> '''<math>\frac{4}{7} x - 5 </math>''' | |||
< | |||
:x - ( | |||
}} | }} | ||
</div> | </div> | ||
<div class="rahmen"> | |||
<big>'''Aufgabe 6'''</big> | |||
[[Datei:BMT 8 2011 A6.jpg|200px|right]] | [[Datei:BMT 8 2011 A6.jpg|200px|right]] | ||
Bei einem Fernsehquiz steht bereits fest, dass der Kandidat Geld gewinnt. Zur Ermittlung des Geldbetrags (in Euro) mischt der Moderator die abgebildeten Karten und legt sie so auf den Tisch, dass die Zahlen nicht sichtbar sind. Der Kandidat zieht nacheinander drei Karten. Die erste gezogene Karte zeigt die Hunderterstelle des Geldbetrags, die zweite die Zehnerstelle und die dritte die Einerstelle. | Bei einem Fernsehquiz steht bereits fest, dass der Kandidat Geld gewinnt. Zur Ermittlung des Geldbetrags (in Euro) mischt der Moderator die abgebildeten Karten und legt sie so auf den Tisch, dass die Zahlen nicht sichtbar sind. Der Kandidat zieht nacheinander drei Karten. Die erste gezogene Karte zeigt die Hunderterstelle des Geldbetrags, die zweite die Zehnerstelle und die dritte die Einerstelle. | ||
'''a)''' Bestimme die Anzahl der Möglichkeiten für den Geldbetrag. | |||
{{Lösung versteckt|1= | |||
:5 · 4 · 3 = '''60''' | :5 · 4 · 3 = '''60''' | ||
}} | }} | ||
'''b)''' Bestimme die Anzahl der Möglichkeiten für den Geldbetrag, wenn dieser über 200 Euro liegen soll. | |||
{{Lösung versteckt|1= | |||
:4 · 4 · 3 = '''48''' | :4 · 4 · 3 = '''48''' | ||
}} | }} | ||
</div> | </div> | ||
<div class="rahmen"> | |||
<div | |||
<big>'''Aufgabe 7'''</big> | <big>'''Aufgabe 7'''</big> | ||
| Zeile 224: | Zeile 167: | ||
Schuhgröße. | Schuhgröße. | ||
'''a)''' Berechne mithilfe der Formel die Fußlänge einer Person mit Schuhgröße 39. | |||
{{Lösung versteckt|1= | |||
:''Auflösen der Formel nach f:'' | :''Auflösen der Formel nach f:'' | ||
::s = (f + 1,5) · 1,5 | ::s = (f + 1,5) · 1,5 | ||
| Zeile 241: | Zeile 180: | ||
:Die Fußlänge beträgt 24,5 cm. | :Die Fußlänge beträgt 24,5 cm. | ||
}} | }} | ||
'''b)''' Die abgebildete Skulptur steht zu Ehren des berühmten Fußballspielers Uwe Seeler vor dem Stadion des Hamburger SV. Der Skulptur kann gemäß obiger Formel eine Schuhgröße zugeordnet werden. | |||
Schätze zunächst die Fußlänge ab; erläutere dein Vorgehen. | Schätze zunächst die Fußlänge ab; erläutere dein Vorgehen. | ||
Ermittle damit näherungsweise die Schuhgröße. | Ermittle damit näherungsweise die Schuhgröße. | ||
[[Datei:BMT 8 2011 A7.jpg|220px|right]] | |||
{{Lösung versteckt|1= | |||
:Schätzwert für die Größe des Mannes: 1,8m | :Schätzwert für die Größe des Mannes: 1,8m | ||
: | : | ||
| Zeile 263: | Zeile 196: | ||
}} | }} | ||
</div> | </div> | ||
[[Kategorie:BMT 8 Mathematik]] | |||
[[Kategorie:Jahrgangsstufentests]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Interaktive Übung]] | |||
Aktuelle Version vom 23. April 2022, 18:01 Uhr
Test und Lösungshinweise zum Download
Aufgabe 1
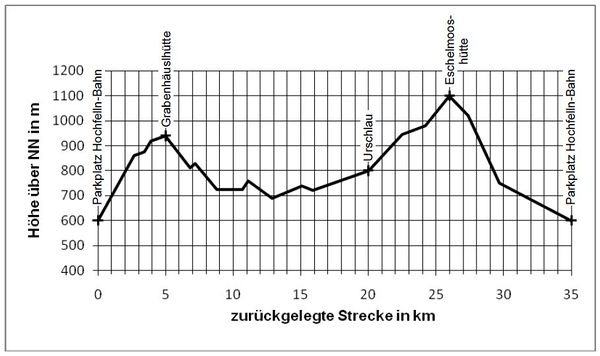
Lukas macht eine Mountainbike-Tour rund um den Hochfelln. Die Abbildung zeigt das Streckenprofil seiner insgesamt 35 km langen Tour, die am Parkplatz der Hochfelln-Bahn beginnt und endet.
a) An der Grabenhäuslhütte merkt Lukas, dass er zu Beginn der Tour vergessen hat, seinen Kilometerzähler auf null zurückzusetzen; er tut dies nun nachträglich. Wie wird der Zählerstand in Urschlau lauten?
b) Nach der Tour stellt Lukas fest: „Bei der Abfahrt von der Eschelmooshütte bis zum Parkplatz habe ich pro Minute 25 Meter an Höhe verloren.“ Berechne, wie lange er für die Abfahrt gebraucht hat und mit welcher Durchschnittsgeschwindigkeit in er die dabei zurückgelegte Strecke gefahren ist.
benötigte Zeit: 500m : 25 = 20 min
Geschwindigkeit: 27c) Welchen Anteil der Höhenmeter, die Lukas insgesamt bergauf bewältigen muss, hat er an der Grabenhäuslhütte ungefähr bereits hinter sich?
(!25 %) (40 %) (!55 %) (!70 %) (!85 %)
Aufgabe 2a
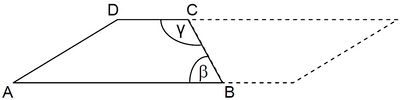
Betrachtet wird ein beliebiges Trapez ABCD mit AB || CD.
(!γ = 90° + β) (β + γ < 360°) (!γ = 2 · β) (β = 180° - γ) (!β < γ)
Aufgabe 2b
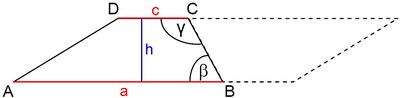
An jedes Trapez ABCD lässt sich ein dazu kongruentes Trapez so anfügen, dass ein Parallelogramm entsteht (vgl. Abbildung). Gib eine Formel an, mit der man allgemein den Flächeninhalt eines Trapezes bestimmen kann. Trage alle verwendeten Benennungen in die Abbildung ein; ergänze die Abbildung geeignet.
Aufgabe 3
In der folgenden Gleichung stehen a und b für rationale Zahlen.
ax = 7x + b
a) Bestimme die Lösung der Gleichung für a = 3 und b = 8 .
- 3x = 7x + 8
- -4x = 8
- x = -2
b) Gib Werte für a und b so an, dass die Gleichung die Lösung x = -5 hat.
- z.B. a = 0, b = 35
c) Gib Werte für a und b so an, dass die Gleichung keine Lösung hat.
- z.B. a = 7, b = 1
- a muss 7 sein, für b können alle Werte außer Null angegeben werden.
Aufgabe 4
Marie möchte alle Punkte markieren, die von A und B den gleichen Abstand haben und gleichzeitig von C weniger als 1,5 cm entfernt sind. Ergänze sinnvoll, was sie sich dazu überlegen könnte.
„Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf ... sowie ... .“
- Um die gesuchten Punkte zu markieren, benötige ich zwei Linien. Die Punkte liegen nämlich auf der Mittelsenkrechten der Strecke [AB] sowie im Inneren des Kreises um C mit Radius 1,5 cm.
Aufgabe 5
Vereinfache jeweils so weit wie möglich.
a)
- Achtung: Hier gilt kein Distributivgesetz!
b)
Aufgabe 6
Bei einem Fernsehquiz steht bereits fest, dass der Kandidat Geld gewinnt. Zur Ermittlung des Geldbetrags (in Euro) mischt der Moderator die abgebildeten Karten und legt sie so auf den Tisch, dass die Zahlen nicht sichtbar sind. Der Kandidat zieht nacheinander drei Karten. Die erste gezogene Karte zeigt die Hunderterstelle des Geldbetrags, die zweite die Zehnerstelle und die dritte die Einerstelle.
a) Bestimme die Anzahl der Möglichkeiten für den Geldbetrag.
- 5 · 4 · 3 = 60
b) Bestimme die Anzahl der Möglichkeiten für den Geldbetrag, wenn dieser über 200 Euro liegen soll.
- 4 · 4 · 3 = 48
Aufgabe 7
In Kontinentaleuropa ist es üblich, Schuhgrößen nach dem „Pariser Stich“ mithilfe der Formel s = (f + 1,5) · 1,5 zu berechnen. Dabei ist f die Fußlänge in cm und s die zugehörige Schuhgröße.
a) Berechne mithilfe der Formel die Fußlänge einer Person mit Schuhgröße 39.
- Auflösen der Formel nach f:
- s = (f + 1,5) · 1,5
- s : 1,5 = f + 1,5
- f = s : 1,5 - 1,5
- Einsetzen des Wertes der Schuhgröße:
- f = 39 : 1,5 - 1,5 = 26 - 1,5 = 24,5
- Die Fußlänge beträgt 24,5 cm.
b) Die abgebildete Skulptur steht zu Ehren des berühmten Fußballspielers Uwe Seeler vor dem Stadion des Hamburger SV. Der Skulptur kann gemäß obiger Formel eine Schuhgröße zugeordnet werden.
Schätze zunächst die Fußlänge ab; erläutere dein Vorgehen.
Ermittle damit näherungsweise die Schuhgröße.
- Schätzwert für die Größe des Mannes: 1,8m
- Schätzwert für Länge des Fußes in cm: 3 · 180cm = 540cm 500cm
- Näherungswert für die Schuhgröße: 500 · 1,5 = 750