Das Lot: Unterschied zwischen den Versionen
Main>Petra Bader Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (61 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{ | {{Navigation verstecken|{{Winkelhalbierende}}|Lernschritte einblenden|Lernschritte ausblenden}} | ||
__NOTOC__ | |||
{{Box|1=Lernpfad|2=<h4>3. Streich: [[Mathematik-digital/Das Lot|Das Lot]]</h4> | |||
===<u>Material:</u>=== | |||
*{{pdf|AB3_Lot.pdf|Arbeitsblatt zum Lot}}|3=Lernpfad}} | |||
== Das Lot errichten == | ==Das Lot errichten== | ||
{| | {| | ||
|''Auf einem ganz bestimmten Punkt''<br> | |''Auf einem ganz bestimmten Punkt''<br> | ||
| Zeile 11: | Zeile 15: | ||
|} | |} | ||
{{Box|1=Aufgabe|2= | |||
# Zeichne auf einem karierten Blatt eine Strecke [AB] mit <math> \overline{AB} = 6 cm</math>. | # Zeichne auf einem karierten Blatt eine Strecke [AB] mit <math> \overline{AB} = 6 cm</math>. | ||
# Wähle einen beliebigen Punkt P auf der Strecke, der die Strecke <u>'''''nicht'''''</u> halbiert und konstruiere eine senkrechte Gerade l auf die Strecke [AB], die durch den Punkt P verläuft! Diese Gerade nennt man '''Lot''' | # Wähle einen beliebigen Punkt P auf der Strecke, der die Strecke <u>'''''nicht'''''</u> halbiert und konstruiere eine senkrechte Gerade l auf die Strecke [AB], die durch den Punkt P verläuft! Diese Gerade nennt man '''Lot'''. | ||
# Formuliere die einzelnen Konstruktionsschritte schriftlich unter Deine Konstruktion! Besprich diese mit Deinem Nachbarn! | # Formuliere die einzelnen Konstruktionsschritte schriftlich unter Deine Konstruktion! Besprich diese mit Deinem Nachbarn! | ||
# Überprüfe Deine Konstruktionsschritte | # Überprüfe Deine Konstruktionsschritte zum Errichten eines Lotes anhand folgender '''[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/grundkonstruktionen/loterrichten.html Animation]'''! | ||
|3=Arbeitsmethode}} | |||
[[Bild:loterrichten.jpg|430px|right]] | |||
{{Box|Definition|Eine Senkrechte durch einen Punkt Q zu einer Geraden g nennt man '''Lot'''. | |||
Eine Senkrechte durch einen Punkt Q zu einer Geraden g nennt man '''Lot'''. | <br>Der Schnittpunkt des Lotes l mit g heißt '''Lotfußpunkt P'''.|Merksatz}} | ||
<br>Der Schnittpunkt des Lotes l mit g heißt '''Lotfußpunkt P'''.}} | |||
{{ | {{Box|Merke| | ||
Gilt P ∈ g, so sagt man auch: Im Punkt P wird das '''Lot''' zu g '''errichtet'''.|Merksatz}} | |||
Gilt P | |||
===Konstruktion: Errichte das Lot im Punkt P auf eine Gerade g (Arbeitsblatt)=== | |||
=== Konstruktion: | |||
{{Box|Aufgabe| | |||
# Übertrage die Definition und die Merkregel vom Lot auf Dein Arbeitsblatt! | |||
# Übertrage die Definition und die Merkregel vom Lot auf Dein Arbeitsblatt! | # Konstruiere auf dem Arbeitsblatt im Punkt P auf der Geraden g das Lot l! Beschrifte Deine Zeichnung (Lot, Lotfußpunkt etc.)! | ||
# Konstruiere auf dem Arbeitsblatt im Punkt P auf der Geraden g das Lot l! Beschrifte Deine Zeichnung (Lot, Lotfußpunkt etc.)! | # Übertrage, die Konstruktionsschritte zum Errichten eines Lotes aus der '''[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/grundkonstruktionen/loterrichten.html Animation]''' auf Dein Arbeitsblatt! | ||
# Übertrage, die | # Welche weiteren Beispiele aus Deiner Alltagswelt für das Lot in einem Punkt kennst Du? | ||
# Welche weiteren Beispiele für | |Arbeitsmethode}} | ||
== Das Lot fällen == | ==Das Lot fällen== | ||
<table><tr><td> | <table><tr><td> | ||
[[Bild:maxhähnchen.jpg|250px]]</td><td>''Durch den Schornstein mit Vergnügen''<br> | [[Bild:maxhähnchen.jpg|250px]]</td><td>''Durch den Schornstein mit Vergnügen''<br> | ||
| Zeile 60: | Zeile 61: | ||
<br> | <br> | ||
'''Welchen "Weg" muss die Angelschnur nehmen, damit Max und Moritz die Hähnchen erangeln können?''' | '''Welchen "Weg" muss die Angelschnur nehmen, damit Max und Moritz die Hähnchen erangeln können?''' | ||
=== | |||
{{Box|1=Aufgabe|2= | |||
# Zeichne auf einem karierten Blatt eine Strecke [AB] mit <math> \overline{AB} = 6 cm</math>. | |||
# Wähle einen beliebigen Punkt P der nicht auf der Strecke [AB] liegt und konstruiere das Lot durch P auf die Gerade [AB]! | |||
# Formuliere die einzelnen Konstruktionsschritte schriftlich unter Deine Konstruktion! Besprich diese mit Deinem Nachbarn! | |||
# Überprüfe Deine Konstruktionsschritte zum Fällen eines Lotes anhand folgender '''[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/grundkonstruktionen/lotfaellen.html Animation]'''! | |||
|3=Arbeitsmethode}} | |||
'''<u> | {{Box|Merke| | ||
# Konstruiere auf | Gilt P <math>\not\in </math> g, so sagt man auch: Im Punkt P wird das '''Lot''' auf g '''gefällt'''.|Merksatz}} | ||
# | |||
# Welche weiteren Beispiele für | |||
===Konstruktion: Fälle das Lot vom Punkt P auf eine Gerade g (Arbeitsblatt)=== | |||
'''<u>Notiere auf Dein Arbeitsblatt:</u>''' | |||
#Übertrage die Merkregel vom Lot auf Dein Arbeitsblatt! | |||
#Konstruiere auf Deinem Arbeitsblatt das Lot auf die Gerade g durch den Punkt P im Kamin! | |||
#Übertrage, die Konstruktionsschritte zum Fällen eines Lotes aus der '''[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/grundkonstruktionen/lotfaellen.html Animation]''' auf Dein Arbeitsblatt! | |||
#Wie nennt man die Länge der Lotstrecke? Notiere auf Dein Arbeitsblatt! (vgl. '''[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/grundkonstruktionen/lotfaellen.html Animation]''') | |||
#Welche weiteren Beispiele für das Fällen des Lotes aus dem Alltag kennst Du? | |||
<br> | <br> | ||
<br> | <br> | ||
'''<u>Konstruieren mit GeoGebra:</u>''' | '''<u>Konstruieren mit GeoGebra:</u>''' | ||
# Speichere folgende {{Ggb|Maxhähnchen.ggb|Datei}} in Deinem Ordner ab! | |||
# Fälle das Lot vom Punkt P auf die Gerade g! Orientiere Dich dabei an den Konstruktionsschritten auf dem Arbeitsblatt! | #Speichere folgende '''{{Ggb|Maxhähnchen.ggb|GeoGebra-Datei}}''' in Deinem Ordner ab! | ||
# Speichere die erstellte Konstruktion unter " | #Fälle das Lot vom Punkt P auf die Gerade g! Orientiere Dich dabei an den Konstruktionsschritten auf dem Arbeitsblatt! | ||
#Speichere die erstellte Konstruktion unter "Haehnchen_<<DeinName>>" im Klassenverzeichnis ab! | |||
<br> | <br> | ||
<br> | <br> | ||
== ''Für besonders flinke Schüler:'' Formuliere eine Aufgabe und konstruiere == | |||
==''Für besonders flinke Schüler:'' Formuliere eine Aufgabe und konstruiere== | |||
{| | {| | ||
| | | | ||
1. Betrachte das nebenstehende Bild und überlege Dir eine Aufgabenstellung, in der man ein Lot konstruieren muss. Beginne beispielsweise mit: | |||
:::Max und Moritz stets bereit | |||
:::gerade in der heißen Sommerzeit... | :::Max und Moritz stets bereit | ||
:::gerade in der heißen Sommerzeit... | |||
|[[Bild: | |||
2. Öffne die '''{{Ggb|boot.ggb |GeoGebra-Datei}}''' und löse Deine erdachte Aufgabe durch Konstruktion des Lotes!<br> | |||
3. Platziere (in der GeoGebra-Datei) das Boot durch Ziehen des gelben Punktes A so, dass es zum Wellenbrecher einen Abstand von 7 Längeneinheiten besitzt! | |||
|[[Bild:bootimwasser.jpg|450px]] | |||
|}<br><br> | |}<br><br> | ||
''' | ==Was sind das nur für rote Linien?== | ||
<br> | |||
<br> | #Öffne folgende '''[http://inmare.cspsx.de/VierDreiecke.html Seite]''' und experimentiere! | ||
#Ergänze die Lücken! | |||
Hast Du alle erkannt? | |||
<br><br> | |||
==Hausaufgabe== | |||
Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:<br> | |||
'''S. 18 Nr 6''' | |||
---- | ---- | ||
{ | |||
{{Winkelhalbierende}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Interaktive Übung]] | |||
Aktuelle Version vom 24. April 2022, 10:06 Uhr
Das Lot errichten
| Auf einem ganz bestimmten Punkt soll er steh'n mit ganz viel Prunk, |
- Zeichne auf einem karierten Blatt eine Strecke [AB] mit .
- Wähle einen beliebigen Punkt P auf der Strecke, der die Strecke nicht halbiert und konstruiere eine senkrechte Gerade l auf die Strecke [AB], die durch den Punkt P verläuft! Diese Gerade nennt man Lot.
- Formuliere die einzelnen Konstruktionsschritte schriftlich unter Deine Konstruktion! Besprich diese mit Deinem Nachbarn!
- Überprüfe Deine Konstruktionsschritte zum Errichten eines Lotes anhand folgender Animation!
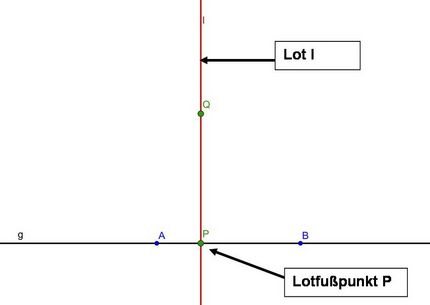
Eine Senkrechte durch einen Punkt Q zu einer Geraden g nennt man Lot.
Der Schnittpunkt des Lotes l mit g heißt Lotfußpunkt P.
Konstruktion: Errichte das Lot im Punkt P auf eine Gerade g (Arbeitsblatt)
- Übertrage die Definition und die Merkregel vom Lot auf Dein Arbeitsblatt!
- Konstruiere auf dem Arbeitsblatt im Punkt P auf der Geraden g das Lot l! Beschrifte Deine Zeichnung (Lot, Lotfußpunkt etc.)!
- Übertrage, die Konstruktionsschritte zum Errichten eines Lotes aus der Animation auf Dein Arbeitsblatt!
- Welche weiteren Beispiele aus Deiner Alltagswelt für das Lot in einem Punkt kennst Du?
Das Lot fällen
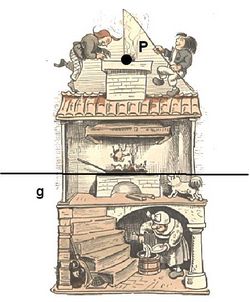
Welchen "Weg" muss die Angelschnur nehmen, damit Max und Moritz die Hähnchen erangeln können?
- Zeichne auf einem karierten Blatt eine Strecke [AB] mit .
- Wähle einen beliebigen Punkt P der nicht auf der Strecke [AB] liegt und konstruiere das Lot durch P auf die Gerade [AB]!
- Formuliere die einzelnen Konstruktionsschritte schriftlich unter Deine Konstruktion! Besprich diese mit Deinem Nachbarn!
- Überprüfe Deine Konstruktionsschritte zum Fällen eines Lotes anhand folgender Animation!
Konstruktion: Fälle das Lot vom Punkt P auf eine Gerade g (Arbeitsblatt)
Notiere auf Dein Arbeitsblatt:
- Übertrage die Merkregel vom Lot auf Dein Arbeitsblatt!
- Konstruiere auf Deinem Arbeitsblatt das Lot auf die Gerade g durch den Punkt P im Kamin!
- Übertrage, die Konstruktionsschritte zum Fällen eines Lotes aus der Animation auf Dein Arbeitsblatt!
- Wie nennt man die Länge der Lotstrecke? Notiere auf Dein Arbeitsblatt! (vgl. Animation)
- Welche weiteren Beispiele für das Fällen des Lotes aus dem Alltag kennst Du?
Konstruieren mit GeoGebra:
- Speichere folgende
 GeoGebra-Datei in Deinem Ordner ab!
GeoGebra-Datei in Deinem Ordner ab! - Fälle das Lot vom Punkt P auf die Gerade g! Orientiere Dich dabei an den Konstruktionsschritten auf dem Arbeitsblatt!
- Speichere die erstellte Konstruktion unter "Haehnchen_<<DeinName>>" im Klassenverzeichnis ab!
Für besonders flinke Schüler: Formuliere eine Aufgabe und konstruiere
|
1. Betrachte das nebenstehende Bild und überlege Dir eine Aufgabenstellung, in der man ein Lot konstruieren muss. Beginne beispielsweise mit:
2. Öffne die |

|
Was sind das nur für rote Linien?
- Öffne folgende Seite und experimentiere!
- Ergänze die Lücken!
Hast Du alle erkannt?
Hausaufgabe
Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:
S. 18 Nr 6