Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(23 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Navigation verstecken|{{Lernpfad Lineare Funktionen}}}}
<div class="grid">
<div class="grid">
  <div class="width-1-6">[[Datei:Power-sports-1015688 1920.jpg|Bankdrücken]]</div>
  <div class="width-1-6">[[Datei:Power-sports-1015688 1920.jpg|Bankdrücken]]</div>
Zeile 8: Zeile 10:




{{Box|5. Wie war das jetzt nochmal?|Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.|Üben}}
<center>[[Datei:Steigungsdreieck A1.png|300px|Bild zur Aufgabe 1]]</center>


{{Box|5. Wie war das jetzt nochmal?|Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
<center>[[Datei:Steigungsdreieck A1.png|300px|Bild zur Aufgabe 1]]</center>
|Üben}}
<div class="lueckentext-quiz">  
<div class="lueckentext-quiz">  
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
Zeile 23: Zeile 23:


{{Box|6. Wie groß ist die Steigung?|
{{Box|6. Wie groß ist die Steigung?|
[[Datei:Browse-1019848 1920.jpg|right|220px|Buch lesen]]
[[Datei:Lernpfad lineare Funktionen Station 2 Übung 6.png|right|500px|Graphen linearer Funktionen]]
Schlage bitte dein Mathebuch auf der '''Seite 47''' auf und betrachte in '''Aufgabe 5''' diejenige Gerade, die zu einer proportionalen Funktion passt. Berechne von dieser einen Geraden die Steigung.
Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.  


* Notiere dein Rechnungen und Überlegung im Übungsheft.
* Notiere dein Rechnungen und Überlegungen im Übungsheft.
* Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
* Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
|Üben}}
|Üben}}


{{Lösung versteckt|1=<span style="color:blue">blaue Gerade: <math>m=\frac{2}{3}</math> </span>}}
{{Lösung versteckt|1=Die lilafarbene Gerade gehört zu einer proportionalen Funktion, da sie durch den Ursprung verläuft.
 
Ihre Steigung ist <math>m=\frac{1}{3}</math>.
 
Zur Berechnung der Steigung kann man z.B. die Punkte <math>O(0 | 0)</math> und <math>A(3 | 1)</math> verwenden.
}}




{{Box|7. Zeichne die Gerade!|
{{Box|7. Zeichne die Gerade!|
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
* a) <math>f(x)=1,5\cdot x</math>
 
* b) <math>g(x)=-\frac{1}{4}\cdot x</math>
a) <math>f(x)=1,5\cdot x</math>
 
b) <math>g(x)=-\frac{1}{4}\cdot x</math>
|Üben}}
|Üben}}
{{Lösung versteckt|Wandle zunächst die Steigung 1,5 in einen Bruch um!|Tipp zu a)|Verbergen}}
{{Lösung versteckt|Wandle zunächst die Steigung 1,5 in einen Bruch um!|Tipp zu a)|Verbergen}}
{{Lösung versteckt|a) [[Datei:Gerade zeichnen 1.png|200px|Steigung 1,5]]
{{Lösung versteckt|a) [[Datei:Gerade zeichnen 1.png|200px|Steigung 1,5]]
b) [[Datei:Gerade zeichnen 2.png|200px|Steigung 1,5]]}}
b) [[Datei:Gerade zeichnen 2.png|200px|Steigung 1,5]]}}
== Doping für Schnelle ==
<span style ="color:blue">Du liegst '''gut in der Zeit?'''</span> [[File:Animated winking Smiley colored.gif|100px|right|Animated winking Smiley colored]]
Dann versuch doch, den armen Radfahrern zu helfen...!
{{Box|8. Tour de France!|[[Datei:Berg Steigung.png|280px|right|Berg Steigung]]
Damit die Radfahrer wissen, wie viel Doping sie zur Tour de France mitnehmen sollen, müssen sie wissen, welche Steigungen im Mittel zu erwarten sind.
Bearbeite dazu die im Übungsheft '''Aufgabe 6 auf Seite 34.'''
Du weißt nicht wie du anfangen sollst?
{{Lösung versteckt|"mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft ''gleichmäßig'' zwischen zwei Punkten.
Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden...|Tipp 1|Tipp verbergen}}
{{Lösung versteckt|Wenn du die Punkte mit je einer Geraden verbunden hast, musst du Steigungsdreiecke einzeichnen und damit die Steigung bestimmen.|Tipp 2|Verbergen}}
{{Lösung versteckt|Legt man den Koordinatenusrprung in den Punkt A so gilt:
[[Datei:Bergsteigung Lsg.png|500px|mittlere Steigungen]]|Lösung der Aufgabe|Lösung verbergen}}
|Üben}}




Zeile 66: Zeile 53:


'''Alles geschafft? Super, dann auf zu Station 3!'''
'''Alles geschafft? Super, dann auf zu Station 3!'''
[[Datei:binoculars-1015267_1920.jpg|150px]] [[../../Station_3|'''...hier geht es weiter''']]'''!'''


{{Fortsetzung|weiter=Station 3|weiterlink=../../Station_3}}




{{Lernpfad Lineare Funktionen}}
[[Kategorie:Funktionen]]
[[Kategorie:Lineare Funktion]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:R-Quiz]]

Aktuelle Version vom 4. Januar 2025, 16:22 Uhr

Steigung 01.png

Lineare Funktionen

Mathematik-digital.de
Bankdrücken


Übung macht den Meister! In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß!


5. Wie war das jetzt nochmal?
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
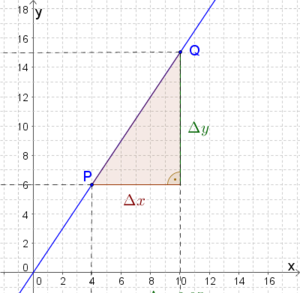
Bild zur Aufgabe 1

Die Steigung m berechnet man mithilfe des Steigungsdreiecks.

y x = (yQyP)(xQxP)(156)(104)1,5

Die Steigung der dargestellten Geraden ist 1,5


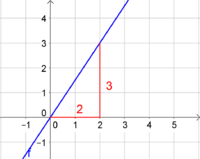
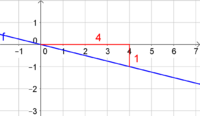
6. Wie groß ist die Steigung?
Graphen linearer Funktionen

Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.

  • Notiere dein Rechnungen und Überlegungen im Übungsheft.
  • Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.

Die lilafarbene Gerade gehört zu einer proportionalen Funktion, da sie durch den Ursprung verläuft.

Ihre Steigung ist .

Zur Berechnung der Steigung kann man z.B. die Punkte und verwenden.


7. Zeichne die Gerade!

Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!

a)

b)

Wandle zunächst die Steigung 1,5 in einen Bruch um!

a) Steigung 1,5

b) Steigung 1,5



Alles geschafft? Super, dann auf zu Station 3!

Station 3
Abgerufen von „https://unterrichten.zum.de/index.php?title=Lineare_Funktionen/Station_2/Übung&oldid=139273“