Lineare Funktionen/Station 3

Navigation anzeigen

Lineare Funktionen

• Station 1: Proportionalität
• Übung 1
• Station 2: Steigung
• Übung 2
• Station 3: Beschreibung allgemeiner Geraden
• Übung 3
• Station 4: Aufstellen eines Funktionterms
• Übung 4
• Abschluss

Mathematik-digital.de

Station 3: Beschreibung allgemeiner Geraden

In Station 2 hast du gelernt, wie man die Steigung von Geraden im Koordinatensystem bestimmen kann.

Allerdings haben wir bislang immer nur solche Geraden betrachtet, die Graph einer proportionalen Funktion waren, also Geraden, die durch den Ursprung verlaufen.

In dieser Station lernst du, wie man beliebige Geraden durch eine Funktionsgleichung beschreiben kann, also auch solche, die keine Ursprungsgeraden sind.

Sind solche Geraden überhaupt relevant?

Starte die App und überlege genau, bevor du die Fragen beantwortest.

Ursprungsgeraden reichen nicht!

Ziehe die Begriffe unten in die richtige Lücke.

Bis jetzt haben wir immer nur Funktionen Zusammenhänge der Form $f(x)=m\cdot x$ betrachtet. Die Graphen zu diesen Funktionen waren immer Geraden, die durch den verlaufen.

Wie du eben gesehen hast, gibt jedoch Situationen, die mit solchen Funktionen und Geraden werden können.

Dies ist vor allem dann der Fall, wenn beim x-Wert 0 der zugehörige y-Wert ist. In unserem Fall bedeutete das, dass zum Zeitpunkt t=0 die zugehörige Wassermenge nicht 0m³, sondern zum Beispiel 400m³ war.

Trotzdem stellt der Graph noch eine dar, da die Wassermenge immer noch zu- oder abnimmt.Diese ist jedoch im Vergleich zur nach oben oder unten verschoben.

Wie aber sieht eine Funktionsgleichung aus, die eine "allgemeine" Gerade richtig beschreiben kann?

UrsprungsgeradenUrsprungnicht mehr beschriebenproportionalernicht gleich 0gleichmäßigGerade

neu starten

Lineare Funktion - Funktionsterm

Wir wissen bereits, wie der Funktionsterm von Funktionen aussieht, deren Graphe eine Ursprungsgerade ist:

$f(x) =m\cdot x.$

Jetzt stellt sich aber die Frage, wie denn dann ein Funktionsterm aussehen muss, der jeder beliebige Gerade beschreiben kann?

Um dies herauszufinden, folge bitte den Anleitungen in der nächsten App. Viel Erfolg!

Ergebnis:

Jede beliebige Gerade im Koordinatensystem kann durch die Funktionsgleichung $f(x)=m\cdot x+t$ beschrieben werden.

Alle diese Funktionen, deren Graph eine Gerade ist und deren Funktionsgleichung die Form $f(x)=m\cdot x+t$ hat, heißen lineare Funktionen.

Merke

Jede Funktion, die durch die Funktiongleichung $f(x)=m\cdot x+t$ beschrieben wird, heißt lineare Funktion. Der Graph einer linearen Funktion ist immer (irgend) eine Gerade.

• Man nennt t den y-Achsenabschnitt der Geraden.
• m bezeichnet die Steigung der Geraden.
  
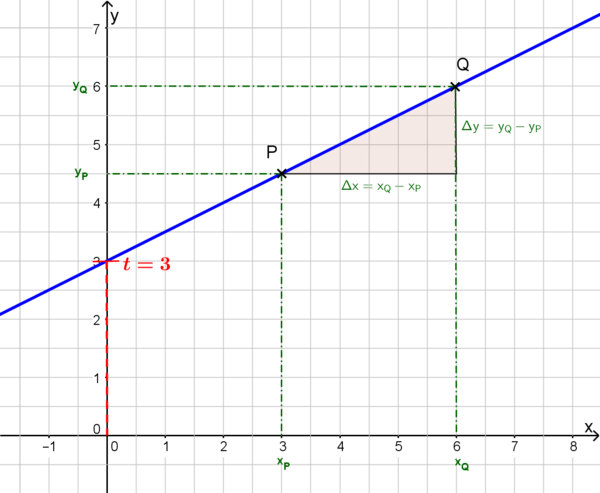
• Verläuft der Graph durch die Punkte P(x_P/y_P) und Q(x_Q/y_Q), so gilt für die Geradensteigung: $m=\frac{y_Q-y_P}{x_Q-x_P}$.

Beispiel Bei obiger Gerade gilt:

• y-Achsenabschnitt: $t = 3$
• Steigung: $m = \frac{6-4,5}{6-3}=\frac{1,5}{3}=0,5$

Damit lautet die Funktionsgleichung: $f(x)=0,5x+3$

Übungen zum Verständnis

10. Ordne zu

Starte die App und entscheide, welche der dargestellten Graphen zu einer linearen Funktion gehören!

Aufgabe 6

Schreibe in den Schulheft hinter jede Aussage, ob sie richtig oder falsch ist. Begründe deine Entscheidung.

• "Jede lineare Funktion ist eine proportionale Funktion."
• "Jeder proportionale Funktion ist eine lineare Funktion."

Lösung anzeigen

Aussage 1 ist falsch.

Grund: Der Graph einer linearen Funktion kann irgendeine Gerade sein, die nicht durch den Ursprung verlaufen muss. Wenn der Graph aber nicht durch den Ursprung verläuft, kann er nicht zu einer proportionalen Funktion gehören.

Aussage 2 ist richtig.

Grund: Der Graph jeder proportionalen Funktion ist eine Ursprungsgerade. Da eine Ursprungsgerade natürlich auch eine Gerade ist, ist die Funktion, zu der der Graph gehört auch eine lineare Funktion.

Text zum Verstecken

11. Finde die Funktionsgleichung!

Starte die App und entscheide, welcher Funktionsterm den dargestellten Graphen richtig beschreibt.

--- aktuelle Meldung: Entwarnung im Bergwerk ---

Das Bergwerk hat ein Gesamtvolumen von 1800m³ und steht bereits völlig unter Wasser, als es endlich gelingt, neue Pumpen in Betrieb zu nehmen. Die neuen Pumpen haben eine max. Pumpleistung von 150m³ Wasser pro Stunde.
Wie lange wird es dauern, bis das Bergwerk wieder frei von Grundwasser ist?

Entscheide für dich selbst, in welchem Schwierigkeitsniveau du die Aufgabe bearbeiten möchtest!

1. Version der Aufgabe - mittlerer Schwierigkeitsgrad

Lösung anzeigen

Aufgabe

a) Welcher der Graphen stellt die beschriebene Situation richtig dar? Begründe deine Entscheidung!

Tipp anzeigen

Identifiziere, welche Angabe aus der Aufgabenstellung dem y-Achsenabschnitt entspricht und welche Angabe der Steigung entspricht! Bei welchem Graph passt beides?

b) Nach wie vielen Stunden ist das Bergwerk vollständig leergepumpt? Begründe deine Antwort.

Tipp anzeigen

Das Bergwerk ist leer, wenn kein Wasser mehr drin ist... ;)

c) Gib die Funktionsgleichung zu der roten Geraden an.

Tipp anzeigen

Du benötigst die Steigung und den y-Achsenabschnitt. Welches Vorzeichen hat die Steigung? ;)

d) Wie groß ist der Funktionswert (y-Wert) zur Zeit $t=12h$?

Lösung anzeigen

Der rote Graph stellt die Situation richtig dar, denn:

• Zu Beginn (t=0) befinden sich 1800m³ Wasser im Bergwerk, also f(0) = 1800
• Innerhalb einer Stunde nimmt die Wassermenge um 150m³ ab. D.h. die Steigung des Graphen ist m = -150.

Daraus folgt die Funktionsgleichung der roten Geraden: $f(t) = -150\cdot t +1800$

Achtung mitdenken: Hier steht t für die Variable (Zeit) nicht für den y-Achsenabschnitt, der ist 1800!

2. Version der Aufgabe - hoher Schwierigkeitsgrad

Lösung anzeigen

Aufgabe

a) Stelle eine Funktionsgleichung auf, die die Situation korrekt beschreibt.

Tipp anzeigen

Identifiziere, welche Angabe aus der Aufgabenstellung dem y-Achsenabschnitt entspricht und welche Angabe der Steigung entspricht! Bei welchem Graph passt beides?

b) Zeichne den Funktionsgraphen zu deiner Funktionsgleichung!

Tipp anzeigen

Die Wassermenge wird weniger! ;)

c) Nach wie vielen Stunden ist das Bergwerk leergepumpt? Findest zu zwei verschiedene Lösungswege?

Tipp anzeigen

1. Lösung mit Hilfe des Graphen

2. Lösung nur mit Hilfe der Funktionsgleichung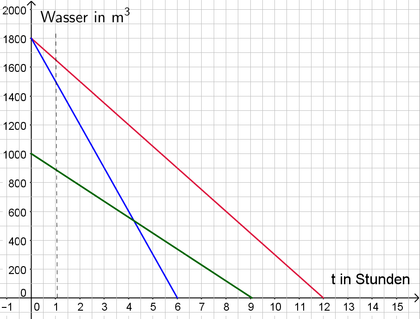

Lösung anzeigen

Der rote Graph im oberen Schaubild stellt die Situation richtig dar, denn:

• Zu Beginn (t=0) befinden sich 1800m³ Wasser im Bergwerk, also f(0) = 1800
• Innerhalb einer Stunde nimmt die Wassermenge um 150m³ ab. D.h. die Steigung des Graphen ist m = -150.

Daraus folgt die Funktionsgleichung der roten Geraden: $f(t) = -150\cdot t +1800$
Achtung mitdenken: Hier steht t für die Variable (Zeit) nicht für den y-Achsenabschnitt, der ist 1800!

Nach 12 Stunden ist das Bergwerk vom Wasser befreit. $f(t)=-150t+1800$ und wenn das Wasser weg ist gilt: $f(t)=0$, also $-150t+1800=0$.

Auflösung der Gleichung liefert: $t=12$

Alle Aufgaben erledigt? Dann kann's weitergehen!

Zur Übung