Kürzen von Brüchen: Unterschied zwischen den Versionen
Main>Katja Heimlich |
Keine Bearbeitungszusammenfassung |
||
| (193 dazwischenliegende Versionen von 14 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
{{Lernpfad | {{Box|1=Lernpfad Brüche kürzen|2= | ||
[[Bild:Comic_Kürzen.gif|right ]] | |||
Das ist ja viel übersichtlicher, wenn man im Zähler und im Nenner nicht so große Zahlen stehen hat,<br> das findest du doch auch, oder?! | |||
== | [[Datei:Logo Mathematik-digital 2011.png|200px|left|verweis=Mathematik-digital]] | ||
|3=Lernpfad}} | |||
{{Navigation verstecken|{{Vorlage:Brüche erweitern, kürzen und vergleichen}}}} | |||
' | ==Station Los geht's, wir machen alles übersichtlicher!== | ||
<div style="margin-left:2em">[https://files.zum.de/lernpfad_brueche/Lernpfad_extern/Kuerzen/Zimmer/zimmer.html In diesem Zimmer] liegt alles herum. Hilf mit, dann geht es schneller. | |||
<br> | |||
Nachdem du beim Zimmeraufräumen geholfen hast, kannst du dich mit deinen Freunden verabreden. <br>[https://files.zum.de/lernpfad_brueche/Lernpfad_extern/Kuerzen/Bonbon/Bonbon.html Sortiere doch schon mal die Süßigkeiten], damit jeder das bekommt, was ihm schmeckt.</div> | |||
Du hast gesehen, dass du aus einem Bruch, wie <math>\frac{6}{18}</math> durch sortieren | |||
oder aufräumen den Bruch <math>\frac{1}{3}</math> zaubern kannst. | |||
<br> | |||
===Aber was steckt hier dahinter?=== | |||
:Dazu schau dir die folgende Aufgabe an. | |||
:Welcher Bruchteil ist zu Beginn blau gefärbt? Welcher Bruchteil ist gefärbt, wenn du das Kästchen drückst? | |||
<ggb_applet height="450" width="900" id="jbhbpmyh" /> | |||
:Damit die Zahlen im Zähler und im Nenner nicht so groß sind, kannst du einzelne Unterteilungen entfernen, aber nicht alle.<br> | |||
:Willst du versuchen, ob du unnötige Unterteilungen entfernen kannst?<br><br> | |||
<div style="margin-left:2em"> [https://files.zum.de/lernpfad_brueche/Lernpfad_extern/Kuerzen/Strecken_entfernen/Strecken_entfernen.html Hier hast du die Möglichkeit, es herauszufinden.]</div> | |||
<br> | <br> | ||
<br> | <br> | ||
== | ==Station Einführung Kürzen== | ||
{{Box|1=Begriff KÜRZEN|2= | |||
[[Bild:Feststellung.gif|left]] | |||
Was du gerade gemacht und beobachtet hast, nennt sich '''Kürzen'''. | Was du gerade gemacht und beobachtet hast, nennt sich '''Kürzen'''. | ||
| Zeile 44: | Zeile 49: | ||
<br> | <br> | ||
< | Wie du gesehen hast, ändert sich auch beim Kürzen der Bruchteil nicht. | ||
<br> | |||
|3=Kurzinfo}} | |||
<br> | <br> | ||
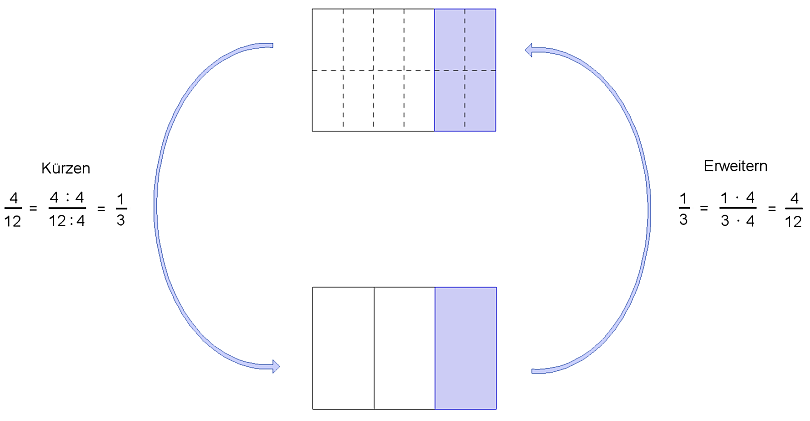
Kommt dir das bekannt vor? {{Lösung versteckt|Kürzen ist das Gegenteil von Erweitern, allerdings mit einigen Besonderheiten.}} | <div style="margin-left:2em">Kommt dir das bekannt vor?? {{Lösung versteckt|<br> Kürzen ist das Gegenteil von Erweitern, allerdings mit einigen Besonderheiten.<br><br> | ||
<center>[[Bild:Bild_erweitern_kürzen.png]]</center>}}</div> | |||
<br> | <br> | ||
<br> | <br> | ||
== | ===Die Rechnung, die dahinter steckt=== | ||
<div style=" | |||
:Hier hast du ein Rechteck. Von dem Rechteck sind <math>\frac{12}{24}</math> blau gefärbt. | |||
:Der Bruchteil lässt sich kürzen, dazu musst du den Schieberegler verschieben. | |||
:Bearbeite nun folgende Aufgaben und schreibe alles auf deinen Laufzettel, du wirst die Antworten noch brauchen. | |||
<div style="margin-left:2em"> | |||
{| | {| | ||
|[[Bild: | |[[Bild:Comic_Frage_klein.gif]] | ||
| | | | ||
<br> | #Welche Zahlen sind zum Kürzen eingestellt? | ||
#Kürze nun mit '''2'''. Wie verändert sich der Zähler? | |||
#Kürze als nächstes mit '''6'''. Wie verändert sich der Nenner? | |||
#Kürze zum Schluss mit '''4'''. Wie verändern sich Zähler und Nenner? | |||
#Überlege dir, warum es die '''5''' nicht auf dem Schieberegler gibt. | |||
|} | |||
<ggb_applet height="450" width="900" id="znzvt9tc" /> | |||
===Quiz: Hast du alle Fragen richtig beantwortet?=== | |||
:Das waren ganz schön viele Fragen! Teste dich selbst, was und wieviel du richtig beantwortet hast.<br> | |||
<div style="margin-left:2em"> [https://files.zum.de/lernpfad_brueche/Ubungen/Quiz/Test_kuerzen/Test_kuerzen.html Hier geht's lang.]<br></div> | |||
<br> | <br> | ||
<br> | |||
==Station Kürzen== | |||
'''Schreibe dir den Merksatz in dein Heft:''' | |||
{{Box|1=Merke|2= | |||
[[Bild:Comic_Merke.gif|left]] | |||
'''Ein Bruch wird gekürzt, indem man den Zähler und den Nenner durch die selbe Zahl dividiert.'''<br> Diese Zahl ist ein '''gemeinsamer Teiler''' von Zähler und Nenner. | |||
<br> | |||
<br> | <br> | ||
Beispiel: <math>\frac{12}{18}=\frac{12 : 6}{18 : 6}=\frac{2}{3}</math> | Beispiel: <math>\frac{12}{18}=\frac{12 : 6}{18 : 6}=\frac{2}{3}</math> | ||
|} | |3=Merksatz}} | ||
<br> | |||
<br> | |||
===Wie oft und mit welchen Zahlen kannst du einen Bruch kürzen?=== | |||
:Kreuze die Antwort an, von der du glaubst, sie sei richtig. | |||
:Wenn du alle Fragen beantwortet hast, klicke auf die '''Korrektur'''-Taste. | |||
<div style="margin-left:2em">Dass die Zahl, mit der du kürzen kannst, ein gemeinsamer Teiler von Zähler und Nenner sein muss,<br> | |||
hast du schon festgestellt. | |||
'''Wie viele gemeinsame Teiler von Zähler und Nenner findest du...''' | |||
<div class="multiplechoice-quiz"> | |||
'''...für den Bruch <math>\frac{4}{8}</math> ?''' (!zwei, nämlich 2 und 4) (!einen, nämlich 4) (drei und zwar 1, 2 und 4) | |||
'''...für den Bruch <math>\frac{1}{8}</math> ?''' (!zwei, nämlich 2 und 4) (einen, nämlich 1) (!keinen) | |||
'''Die 1 ist immer ein gemeinsamer Teiler von Zähler und Nenner, denn jede Zahl ist durch 1 teilbar.''' <br>'''Was machst du, wenn du keinen gemeinsamen Teiler außer 1 findest?''' (Ich kann zwar mit 1 kürzen, aber der Bruch ändert sich dadurch nicht.) (!Das passiert nicht. Man findet immer noch weitere gemeinsame Teiler!) | |||
'''Kannst du mit 0 kürzen?''' (!Ja) (Nein) | |||
</div> | |||
</div> | |||
<br> | |||
<br> | |||
:Das ist wichtig, bitte schreibe dir den folgenden Merksatz in dein Heft. | |||
<div style="margin-left:2em"> | |||
<!--{{Lösung versteckt|1=Text zum Verstecken|2=Label fürs Anzeigen|3=Label fürs Verbergen}}--> | |||
{{Lösung versteckt|1= | |||
{{Box|1=Merke|2= | |||
[[Bild:Comic_Merke.gif| left]] | |||
<br> Kannst du außer 1 keinen gemeinsamen Teiler von Zähler und Nenner finden,<br> dann heißt der Bruch '''vollständig gekürzt'''.<br> Du kannst dann den Bruch nicht weiter vereinfachen oder übersichtlicher machen.<br> | |||
<br><br> | |||
Beispiel: | |||
<math>\frac{4}{6}</math> kann noch mit '''2''' gekürzt werden: <math>\frac{4}{6}=\frac{4 : 2}{6 : 2}=\frac{2}{3}</math> . | |||
<math>\frac{2}{3}</math> hat außer 1 keinen weiteren gemeinsamen Teiler für Zähler und Nenner und ist vollständig gekürzt. | |||
|3=Merksatz}} | |||
|2=Anzeigen|3=Verstecken}}</div> | |||
<br> | |||
<br> | |||
===Wie kannst du einen Bruch vollständig kürzen?=== | |||
<div style="margin-left:2em">[https://files.zum.de/lernpfad_brueche/Lernpfad_extern/Kuerzen/Schrittweise_kuerzen/schrittweisekuerzen.html Finde es heraus!] </div> | |||
<br><br> | |||
{{Box|1=Vorgehensweise KÜRZEN|2= | |||
[[Bild:Feststellung.gif|left]] | |||
<br> | |||
Um einen Bruch vollständig zu kürzen, kürzt du solange mit gemeinsamen Teilern <br> von Zähler und Nenner, bis du keinen außer 1 mehr findest. | |||
|3=Kurzinfo}} | |||
<br><br> | |||
===Die Zeit läuft ab jetzt...=== | |||
<div style="margin-left:2em">[[Bild:Uhr-7.gif|left]] | |||
In einer Stegreifaufgabe oder in einer Schulaufgabe ist die Zeit knapp! | |||
Wenn du kürzen sollst, dann musst du dem Zähler und dem Nenner einen gemeinsamen Teiler ansehen. | |||
Aber erinnerst du dich noch an die [[Teilbarkeitsregeln|Teilbarkeitsregeln]]? | |||
Sie können dir helfen einen gemeinsamen Teiler schneller zu sehen. | |||
<br> | |||
Jetzt solltest du fit sein und gemeinsame Teiler auch in kurzer Zeit finden können. | |||
<br> | |||
<br> | |||
</div> | </div> | ||
<br><br> | |||
==Übungen zum Thema "Brüche kürzen"== | |||
Es gibt mehrere Aufgaben und Schwierigkeiten zur Auswahl. Wir empfehlen dir: Wähle zwei Übungen aus jeder Schwierigkeitsstufe, die du bearbeitest. | |||
<br /><br /><br /> | |||
<div class="grid" style="margin-left:20px"><div class="width-1-3" style="text-align:center; padding:0px 0px 30px 0px;"><div style="background:#8FCD25;line-height:75%;"><br />'''LEICHT'''<br /><br /></div> | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Ubungen_kuerzen/kuerzeMit/kuerzeMit.html Kürze den Bruch] | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Ubungen_kuerzen/kuerzZahl/findediezahl-kuerzen.html Mit welcher Zahl wurde gekürzt?] | |||
</div><div class="width-1-3" style="text-align:center; padding:0px 0px 30px 0px;"><div style="background:#DD7F28;line-height:75%;"><br />'''MITTELSCHWER'''<br /><br /></div> | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Ubungen_kuerzen/kuerzeMit/kuerzeMit_mittel.html Kürze den Bruch] | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Quiz/mit%20welcher%20zahl%20gekuerzt/quiz_bildgekuerzt_leicht.html Mit welcher Zahl wurde gekürzt?] | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Quiz/rof_k/quiz_rof_k.html Wurde richtig gekürzt?] | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Ubungen_kuerzen/vollstaendig%20kuerzen/kuerzevollst.html Kürze vollständig] | |||
</div><div class="width-1-3" style="text-align:center; padding:0px 0px 30px 0px;"><div style="background:#C64285;line-height:75%;"><br />'''SCHWER'''<br /><br /></div> | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Quiz/mit%20welcher%20zahl%20gekuerzt/quiz_bildgekuerzt.html Mit welcher Zahl wurde gekürzt?] | |||
[https://files.zum.de/lernpfad_brueche/Ubungen/Ubungen_kuerzen/vollstaendig%20kuerzen/kuerzevollst-schwer.html Kürze vollständig] | |||
</div></div> | |||
{{Fortsetzung|weiter=Brüche vergleichen|weiterlink=Größenvergleich von Brüchen}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Lernpfad]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:Algebra]] | |||
Aktuelle Version vom 24. April 2022, 10:29 Uhr
Station Los geht's, wir machen alles übersichtlicher!
Sortiere doch schon mal die Süßigkeiten, damit jeder das bekommt, was ihm schmeckt.
Du hast gesehen, dass du aus einem Bruch, wie durch sortieren
oder aufräumen den Bruch zaubern kannst.
Aber was steckt hier dahinter?
- Dazu schau dir die folgende Aufgabe an.
- Welcher Bruchteil ist zu Beginn blau gefärbt? Welcher Bruchteil ist gefärbt, wenn du das Kästchen drückst?

- Damit die Zahlen im Zähler und im Nenner nicht so groß sind, kannst du einzelne Unterteilungen entfernen, aber nicht alle.
- Willst du versuchen, ob du unnötige Unterteilungen entfernen kannst?
Station Einführung Kürzen
Die Rechnung, die dahinter steckt
- Hier hast du ein Rechteck. Von dem Rechteck sind blau gefärbt.
- Der Bruchteil lässt sich kürzen, dazu musst du den Schieberegler verschieben.
- Bearbeite nun folgende Aufgaben und schreibe alles auf deinen Laufzettel, du wirst die Antworten noch brauchen.

Quiz: Hast du alle Fragen richtig beantwortet?
- Das waren ganz schön viele Fragen! Teste dich selbst, was und wieviel du richtig beantwortet hast.
Station Kürzen
Schreibe dir den Merksatz in dein Heft:
Wie oft und mit welchen Zahlen kannst du einen Bruch kürzen?
- Kreuze die Antwort an, von der du glaubst, sie sei richtig.
- Wenn du alle Fragen beantwortet hast, klicke auf die Korrektur-Taste.
hast du schon festgestellt.
Wie viele gemeinsame Teiler von Zähler und Nenner findest du...
...für den Bruch ? (!zwei, nämlich 2 und 4) (!einen, nämlich 4) (drei und zwar 1, 2 und 4)
...für den Bruch ? (!zwei, nämlich 2 und 4) (einen, nämlich 1) (!keinen)
Die 1 ist immer ein gemeinsamer Teiler von Zähler und Nenner, denn jede Zahl ist durch 1 teilbar.
Was machst du, wenn du keinen gemeinsamen Teiler außer 1 findest? (Ich kann zwar mit 1 kürzen, aber der Bruch ändert sich dadurch nicht.) (!Das passiert nicht. Man findet immer noch weitere gemeinsame Teiler!)
Kannst du mit 0 kürzen? (!Ja) (Nein)
- Das ist wichtig, bitte schreibe dir den folgenden Merksatz in dein Heft.
Kannst du außer 1 keinen gemeinsamen Teiler von Zähler und Nenner finden,
dann heißt der Bruch vollständig gekürzt.
Du kannst dann den Bruch nicht weiter vereinfachen oder übersichtlicher machen.
Beispiel:
kann noch mit 2 gekürzt werden: .
hat außer 1 keinen weiteren gemeinsamen Teiler für Zähler und Nenner und ist vollständig gekürzt.
Wie kannst du einen Bruch vollständig kürzen?
Die Zeit läuft ab jetzt...
In einer Stegreifaufgabe oder in einer Schulaufgabe ist die Zeit knapp!
Wenn du kürzen sollst, dann musst du dem Zähler und dem Nenner einen gemeinsamen Teiler ansehen.
Aber erinnerst du dich noch an die Teilbarkeitsregeln?
Sie können dir helfen einen gemeinsamen Teiler schneller zu sehen.
Jetzt solltest du fit sein und gemeinsame Teiler auch in kurzer Zeit finden können.
Übungen zum Thema "Brüche kürzen"
Es gibt mehrere Aufgaben und Schwierigkeiten zur Auswahl. Wir empfehlen dir: Wähle zwei Übungen aus jeder Schwierigkeitsstufe, die du bearbeitest.
MITTELSCHWER