Einführung in quadratische Funktionen/Übungen 3: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Martin Schendzielorz
Keine Bearbeitungszusammenfassung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(54 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
{{Navigation verstecken|
[[Einführung_in_quadratische_Funktionen|Einführung]] - [[Quadratische_Funktionen_-_Bremsweg|Bremsweg]] - [[Quadratische_Funktionen_-_Bremsbeschleunigung|Unterschiedliche Straßenverhältnisse]] - [[Quadratische_Funktionen_-_Übungen1|Übungen 1]] - [[Quadratische_Funktionen_-_Anhalteweg|Anhalteweg]] - [[Quadratische_Funktionen_-_Übungen2|Übungen 2]] - [[Quadratische_Funktionen_-_Stationenbetrieb|Stationenbetrieb]] - [[Quadratische_Funktionen_-_allgemeine quadratische Funktion|Allgemeine quadratische Funktion]] - [[Quadratische_Funktionen_-_Übungen3|Übungen 3]]
{{Einführung in quadratische Funktionen}}
</div>
|Lernschritte einblenden
|Lernschritte ausblenden
}}


__NOTOC__
==Welche Funktionsgleichung stimmt?==


<center><span style="background:#FFFACD">Falls es Probleme mit der Ansicht gibt, bitte [[:zw:Firefox|Firefox]] als Browser verwenden!</span></center>
{|
|-
|<div style="padding:10px;background:#ffffff;border:1px ;">
<big>'''Aufgabe 1: Funktionsterm finden'''</big>
{|
|width=300px|


<div class="grid">
<div class="width-1-3">
Die Parabel hat die Funktionsgleichung  
Die Parabel hat die Funktionsgleichung  


'''f(x) = ax<sup>2</sup> + bx + c'''.
'''f(x) = ax<sup>2</sup> + bx + c'''.


Welcher Funktionsterm passt?
Welche Gleichung passt?
<div class="multiplechoice-quiz">
<div class="multiplechoice-quiz">


(-0,5x<sup>2</sup> + 2x - 1) (!0,5x<sup>2</sup> - 2x + 3)  (!-2x<sup>2</sup> + 8x - 7) (!-0,5x<sup>2</sup> + 2x + 1) (!0,5x<sup>2</sup> - 2x - 1)  
(y = - 0,5x<sup>2</sup> + 2x - 1) (!y = 0,5x<sup>2</sup> - 2x + 3)  (!y = -2x<sup>2</sup> + 8x - 7) (!y = -0,5x<sup>2</sup> + 2x + 1) (!y = 0,5x<sup>2</sup> - 2x - 1)  
</div>
</div>
 
</div>
|width=20px|<!--Diese Spalte bleibt leer und legt den Abstand zwischen Text und Bild fest-->
<div class="width-2-3">
|valign="top" |
[[Bild:Üb3_Parabel_5.jpg|380px]]
[[Bild:Üb3_Parabel_5.jpg|380px]]
</div>
</div>
</div>


|}
<br><br>


<div style="padding:10px;background:#ffffff;border:1px ;">
==Gleichung und Graph zuordnen==
<big>'''Aufgabe 2: Term und Graph zuordnen'''</big>


'''Ordne den Funktionsgraphen den richtigen Term zu.'''
Ordne den Funktionsgraphen die richtigen Gleichung zu.
<div class="lueckentext-quiz">
<div class="lueckentext-quiz">
{|  
{|  
Zeile 39: Zeile 35:
| [[Bild:Üb3_Parabel_1.jpg]] || [[Bild:Üb3_Parabel_3.jpg]] || [[Bild:Üb3_Gerade_1.jpg]] ||  [[Bild:Üb3_Parabel_4.jpg|150px]] || [[Bild:Üb3_Gerade_2.jpg|150px]] || [[Bild:Üb3_Parabel_2.jpg|150px]]  
| [[Bild:Üb3_Parabel_1.jpg]] || [[Bild:Üb3_Parabel_3.jpg]] || [[Bild:Üb3_Gerade_1.jpg]] ||  [[Bild:Üb3_Parabel_4.jpg|150px]] || [[Bild:Üb3_Gerade_2.jpg|150px]] || [[Bild:Üb3_Parabel_2.jpg|150px]]  
|-  
|-  
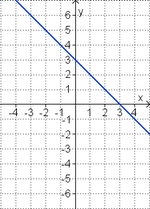
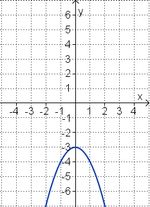
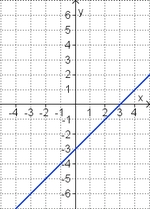
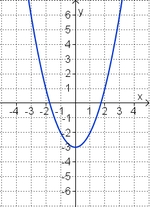
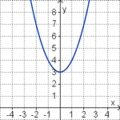
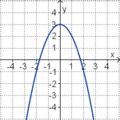
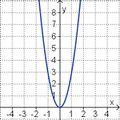
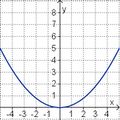
| <strong> x<sup>2</sup> + 3 </strong>  || <strong> -x<sup>2</sup> + 3 </strong> || <strong> -x + 3 </strong> || <strong> -x<sup>2</sup> - 3</strong> || <strong> x - 3 </strong> || <strong> x<sup>2</sup> - 3</strong>
| <strong>y = x<sup>2</sup> + 3 </strong>  || <strong>y = - x<sup>2</sup> + 3 </strong> || <strong>y = - x + 3 </strong> || <strong>y = - x<sup>2</sup> - 3</strong> || <strong>y = x - 3 </strong> || <strong>y = x<sup>2</sup> - 3</strong>
|}
|}


</div></div>
</div>
<br><br>
 
 


<div style="padding:10px;background:#ffffff;border:1px ;">
==Kreuze jeweils alle richtigen Aussagen an==
<big>'''Aufgabe 3: Multiple Choice'''</big>


'''Kreuze jeweils alle richtigen Aussagen an.'''
<div class="multiplechoice-quiz">
<div class="multiplechoice-quiz">


Zeile 61: Zeile 56:


'''Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind?'''  (7x<sup>2</sup> und -7x<sup>2</sup>) (!7x<sup>2</sup> - 2x und 7x<sup>2</sup> + 2x) (!7x<sup>2</sup> - 2 und 7x<sup>2</sup> + 2) (7x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2) (!7x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2x)  
'''Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind?'''  (7x<sup>2</sup> und -7x<sup>2</sup>) (!7x<sup>2</sup> - 2x und 7x<sup>2</sup> + 2x) (!7x<sup>2</sup> - 2 und 7x<sup>2</sup> + 2) (7x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2) (!7x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2x)  
</div></div>
</div>


<br><br>


<div style="padding:10px;background:#ffffff;border:1px ;">
==Memo-Quiz==
<big>'''Aufgabe 4: Memo-Quiz'''</big>


Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).


:::{|border="0" cellspacing="0" cellpadding="4"
|align = "left" width="600"|
<div class="memo-quiz">
<div class="memo-quiz">


{|  
{|  
|-
|-
| <big> '''f(x) = x<sup>2</sup> + 3'''</big>  || [[Bild:Üb3_Parabel_1a.jpg|120px]]  
| <big> '''y = x<sup>2</sup> + 3'''</big>  || [[Bild:Üb3_Parabel_1a.jpg|120px]]  
|-
|-
| <big> '''f(x) = -x<sup>2</sup> + 3'''</big>  || [[Bild:Üb3_Parabel_3a.jpg|120px]]
| <big> '''y = -x<sup>2</sup> + 3'''</big>  || [[Bild:Üb3_Parabel_3a.jpg|120px]]
|-
|-
| <big> '''f(x) = 3x<sup>2</sup>'''</big> || [[Bild:Parabel_a_3a.jpg|120px]]  
| <big> '''y = 3x<sup>2</sup>'''</big> || [[Bild:Parabel_a_3a.jpg|120px]]  
|-
|-
| <big> '''f(x) = 0,2x<sup>2</sup>'''</big>  || [[Bild:Parabel_a_0_2a.jpg|120px]]
| <big> '''y = 0,2x<sup>2</sup>'''</big>  || [[Bild:Parabel_a_0_2a.jpg|120px]]
|-
|-
| <big> '''f(x) = x<sup>2</sup> + 2x''' </big> || [[Bild:Üb3_Parabel_6.jpg|120px]]  
| <big> '''y = x<sup>2</sup> + 2x''' </big> || [[Bild:Üb3_Parabel_6.jpg|120px]]  
|-
|-
| <big> '''f(x) = –x<sup>2</sup> + 2x'''</big>  || [[Bild:Üb3_Parabel_7.jpg|120px]]  
| <big> '''y = –x<sup>2</sup> + 2x'''</big>  || [[Bild:Üb3_Parabel_7.jpg|120px]]  
|-
|-
| <big> '''f(x) = x<sup>2</sup> – 2x – 3''' </big> || [[Bild:Üb3_Parabel_8.jpg|120px]]
| <big> '''y = x<sup>2</sup> – 2x – 3''' </big> || [[Bild:Üb3_Parabel_8.jpg|120px]]
|-
|-
| <big> '''f(x) = –x<sup>2</sup> – 2x + 3'''</big>  || [[Bild:Üb3_Parabel_9.jpg|120px]]  
| <big> '''y = –x<sup>2</sup> – 2x + 3'''</big>  || [[Bild:Üb3_Parabel_9.jpg|120px]]  
|}
|}


Zeile 96: Zeile 87:




|}
</div>


<big>'''Aufgabe 5: Verschiebung und Streckung'''</big><br />
== *Zusatz: Weitere interaktive Übungen ==


*[http://www.mathe-online.at/galerie/fun1/funscribble/index.html Zeichne den Graphen]
*[http://www.zum.de/dwu/depothp/hp-math/hpmqf12.htm Übung 1]


Eine Parabel der Form ax²+bx+c wird <br />
a) '''in y- Richtung verschoben'''
und
b) '''in y- Richtung gestreckt.''' <br />
Welche Eigenschaften der Parabel bleiben erhalten, welche ändern sich?''' <br />
(Hinweis: Diskutiere mit deinem Partner und zeichne dir zur Hilfe eine Parabel auf und verschiebe bzw. strecke sie!)<br />
:{{Lösung versteckt|1=
a)<center> Verschiebung in y- Richtung:
Die Form bleibt erhalten, der y- Wert des Scheitels ändert sich. Die Achsenschnittpunkte ändern sich. <br />
f(x) ist die blaue Funktion, g(x) stellt die rote Funktion dar.
[[Bild:nator1.png|250px]]<br />


b) Streckung in y- Richtung:
Schnittpunkte mit der x- Achse bleiben unverändert. Die Form und der y- Wert des Scheitelpunktes ändert sich. Schnittpunkt mit der y- Achse ändert sich. <br />
[[Bild:nator2.png|250px]]


}}
== Weiterführende Links ==
* [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer]




----


== *Zusatz: Weitere interaktive Übungen ==
{{Einführung in quadratische Funktionen}}
 
*[http://www.mathe-online.at/galerie/fun1/funscribble/index.html Zeichne den Graphen]
*[http://www.zum.de/dwu/depothp/hp-math/hpmqf12.htm Übung 1]




{{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]]}}
[[Kategorie:Interaktive Übung]]
[[Kategorie:R-Quiz]]

Aktuelle Version vom 29. März 2022, 22:23 Uhr

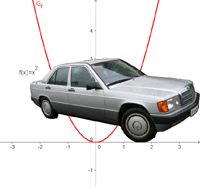
Parabelbremse

Einführung in quadratische Funktionen

  1. Bremsweg
  2. Unterschiedliche Straßenverhältnisse
  3. Übungen 1
  4. Anhalteweg
  5. Übungen 2
  6. Allgemeine quadratische Funktion
  7. Übungen 3

Mathematik-digital.de


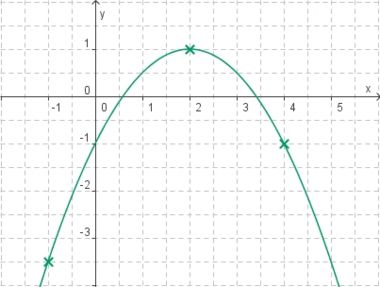
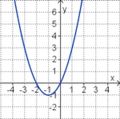
Welche Funktionsgleichung stimmt?

Die Parabel hat die Funktionsgleichung

f(x) = ax2 + bx + c.

Welche Gleichung passt?

(y = - 0,5x2 + 2x - 1) (!y = 0,5x2 - 2x + 3) (!y = -2x2 + 8x - 7) (!y = -0,5x2 + 2x + 1) (!y = 0,5x2 - 2x - 1)

Üb3 Parabel 5.jpg


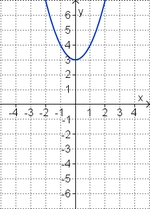
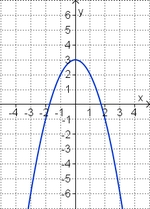
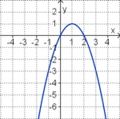
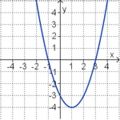
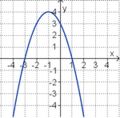
Gleichung und Graph zuordnen

Ordne den Funktionsgraphen die richtigen Gleichung zu.

Üb3 Parabel 1.jpg Üb3 Parabel 3.jpg Üb3 Gerade 1.jpg Üb3 Parabel 4.jpg Üb3 Gerade 2.jpg Üb3 Parabel 2.jpg
y = x2 + 3 y = - x2 + 3 y = - x + 3 y = - x2 - 3 y = x - 3 y = x2 - 3


Kreuze jeweils alle richtigen Aussagen an

f(x) = –2x2 + 3x – 4 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.)


Welche Terme gehören zu einer Funktion, deren Graph symmetrisch zur y-Achse ist? (7x2) (7x2 - 2) (7x2 + 3) (!7x2 - 2x) (!7x2 + 3x) (!7x2 - 2x + 3)


Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x2 und -7x2) (7x2 - 2x und 7x2 + 2x) (!7x2 - 2x und -7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (-7x2 + 2x und -7x2 - 2x)


Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind? (7x2 und -7x2) (!7x2 - 2x und 7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (7x2 - 2 und -7x2 + 2) (!7x2 - 2 und -7x2 + 2x)


Memo-Quiz

Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).

y = x2 + 3 Üb3 Parabel 1a.jpg
y = -x2 + 3 Üb3 Parabel 3a.jpg
y = 3x2 Parabel a 3a.jpg
y = 0,2x2 Parabel a 0 2a.jpg
y = x2 + 2x Üb3 Parabel 6.jpg
y = –x2 + 2x Üb3 Parabel 7.jpg
y = x2 – 2x – 3 Üb3 Parabel 8.jpg
y = –x2 – 2x + 3 Üb3 Parabel 9.jpg


*Zusatz: Weitere interaktive Übungen


Weiterführende Links


Parabelbremse

Einführung in quadratische Funktionen

  1. Bremsweg
  2. Unterschiedliche Straßenverhältnisse
  3. Übungen 1
  4. Anhalteweg
  5. Übungen 2
  6. Allgemeine quadratische Funktion
  7. Übungen 3

Mathematik-digital.de

Abgerufen von „https://unterrichten.zum.de/index.php?title=Einführung_in_quadratische_Funktionen/Übungen_3&oldid=123343“