Einführung in quadratische Funktionen/Übungen 2

Lernschritte einblenden

Einführung in quadratische Funktionen

1. Bremsweg
2. Unterschiedliche Straßenverhältnisse
3. Übungen 1
4. Anhalteweg
5. Übungen 2
6. Allgemeine quadratische Funktion
7. Übungen 3

Mathematik-digital.de

1. Anhalteweg

Die Funktion s(v) = 0,1v² + 1,5v ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt.

1. Welchen Wert hat in diesem Beispiel die Reaktionszeit t_R?
2. Welchen Wert hat die Bremsbeschleunigung a_B?
3. Wie lang ist der Anhalteweg bei einer anfänglichen Geschwindigkeit von 72 km/h (also 20 m/s)?
4. Wie könnte der Anhalteweg verringert werden?

Lösung anzeigen

1. 1,5v steht für den Reaktionsweg, d.h. t_R = 1,5 s
2. $\frac{1}{2a_B} = 0,1$ <=> $\frac{1}{2a_B} = \frac{1}{10}$ <=> 2a_B = 10 <=> a_B = 5 (m/s²)
3. s(20) = 0,1·20² + 1,5·20 = 40 + 30 = 70 (m)
4. Bremsbeschleunigung erhöhen (besserer Fahrbahnbelag, gute Reifen), Reaktionszeit verringern (erhöhte Aufmerksamkeit, Bremsentechnik), Geschwindigkeit reduzieren

2. Bestimme a und b

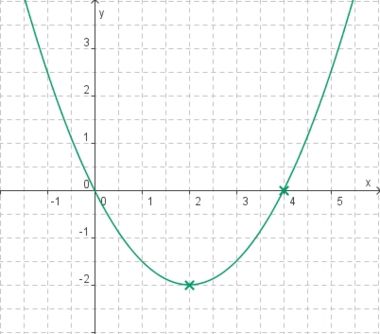
Die Parabel hat die Funktionsgleichung f(x) = ax² + bx. Finde heraus, welche Werte a und b besitzen und erkläre wie du vorgegangen bist.

Hilfe

Lies die Koordinaten zweier Punkte aus dem Graphen ab und setze sie in die Funktionsgleichung ein.

Lösung anzeigen

Die Punkte (4/0) und (2/-2) liegen auf der Parabel, es gilt also

• 0 = a·4² + b·4 --> b = - 4a
• - 2 = a·2² + b·2 --> b = -1 - 2a

daraus folgt -4a = -1 -2a --> a = 0,5 und b = - 2

3. Term und Graph zuordnen

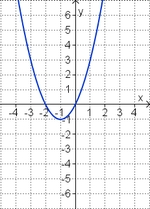
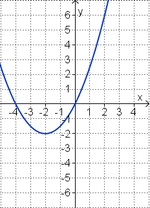
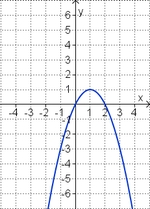
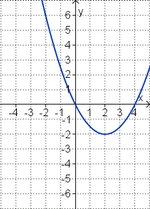
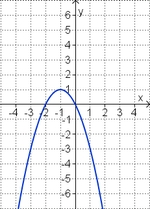
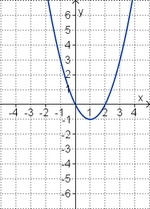
Ordne den Funktionsgraphen den richtigen Term zu.

y = x² + 2xy = -x² + 2xy = x² - 2xy = -x² - 2xy = 0,5x² - 2xy = 0,5x² + 2x

neu starten

4. Kreuze jeweils alle richtigen Aussagen an.

<b>f

1. Die Parabel ist enger als die Normalparabel.
2. Die Parabel ist nach unten geöffnet.
3. x
4. Der Punkt [2|5] liegt auf dem Graphen.
5. Der Punkt [2|7] liegt auf dem Graphen.
6. Die Parabel ist nach oben geöffnet.
7. Die Parabel ist weiter als die Normalparabel.

<b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?</b>

1. -7x² + 2x und -7x² - 2x
2. 7x² und -7x²
3. 7x² - 2 und 7x² + 2
4. 7x² - 2 und 7x² + 2x
5. 7x² - 2x und 7x² + 2x
6. 7x² - 2x und -7x² + 2x

<b>f

1. Die Parabel ist weiter als die Normalparabel.
2. Der Punkt [-1|-2] liegt auf dem Graphen.
3. x
4. Die Parabel ist nach unten geöffnet.
5. Die Parabel ist nach oben geöffnet.
6. Die Parabel ist enger als die Normalparabel.
7. Der Punkt [-1|6] liegt auf dem Graphen.

prüfen!

neu starten

Als nächstes lernst du die allgemeine quadratische Funktion kennen.

Allgemeine quadratische Form