Main>Reinhard Schmidt |
|
| (131 dazwischenliegende Versionen von 17 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| Dieser Lernpfad bietet einen Einstieg das wichtige Thema "Quadratische Funktionen".
| | {{Box|Lernpfad| |
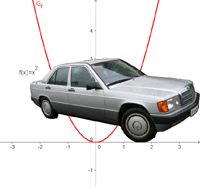
| Die Einführung in das Thema soll am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges erfolgen. Der Lernpfand enthält eine Reihe von interaktiven Übungen, insbesondere auch einige GeoGebra-Applets.
| |
|
| |
|
| {{Kompetenzen|
| | Die Einführung in das Thema "'''Quadratische Funktionen'''" erfolgt am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges. Nachdem auf diese Weise der Begriff der reinquadratischen Funktion erarbeitet worden ist, wird die allgemeine Form vor allem durch Experimentieren am Graphen erarbeitet. |
|
| |
|
| VORHER=
| | Interaktive Übungen tragen zum Verständnis bei und helfen das Erarbeitete zu festigen. |
| | |
| | [[Datei:Logo Mathematik-digital 2011.png|200px|right|verweis=Mathematik-digital|Mathematik-digital]] |
| | |Lernpfad}} |
| | |
| | |
| | {{Einführung in quadratische Funktionen}} |
| | |
| | <div class="zum-hintergrund-grau zum-farbe-x-heller zum-block"> |
| | ===Kompetenzen=== |
| | {{3Spalten| |
| | ==== Das kannst Du schon ==== |
| *Bei linearen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln | | *Bei linearen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln |
| *Parameter variieren und die Auswirkung dieser Variation beschreiben (Handhabung von GeoGebra) | | *Parameter variieren und die Auswirkung dieser Variation beschreiben (Handhabung von GeoGebra) |
| *von der graphischen Darstellung unmittelbar auf die Darstellung als Formel schließen | | *von der graphischen Darstellung unmittelbar auf die Darstellung als Formel schließen |
| *Eigenschaften linearer Funktionen aus der Termdarstellung ablesen und sie begründen | | | *Eigenschaften linearer Funktionen aus der Termdarstellung ablesen und sie begründen |
| NACHHER=
| | |
| | | |
| | ==== Das kannst Du lernen ==== |
| *Übersetzen von einer Realsituation in ein mathematisches Modell | | *Übersetzen von einer Realsituation in ein mathematisches Modell |
| *Parabeln als Graphen quadratischer Funktionen identifizieren | | *Parabeln als Graphen quadratischer Funktionen identifizieren |
| *Bei quad. Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln | | *Bei quadratischen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln |
| *Parameter variieren und die Auswirkung dieser Variation beschreiben | | *Parameter variieren und die Auswirkung dieser Variation beschreiben |
| | |
| }}
| |
| | |
| == Graphische Darstellung ==
| |
| | |
| Die Polizei hat Messungen durchgeführt, um den Zusammenhang zwischen der Geschwindigkeit eines Autos und seinem Bremsweg zu erkunden. Klar ist: Je schneller eine Auto fährt, desto länger ist sein Bremsweg. Aber ist das wirklich so einfach...?
| |
| | |
| Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat:
| |
| | |
| {|border="2" cellspacing="0" cellpadding="4" width="200"
| |
| |align = "right"|'''Geschwindigkeit (in km/h)'''
| |
| |align = "right"|<font size = "3">10</font>
| |
| |align = "right"|<font size = "3">20</font>
| |
| |align = "right"|<font size = "3">30</font>
| |
| |align = "right"|<font size = "3">40</font>
| |
| |align = "right"|<font size = "3">50</font>
| |
| |align = "right"|<font size = "3">80</font>
| |
| |align = "right"|<font size = "3">100</font>
| |
| |align = "right"|<font size = "3">120</font>
| |
| | |
| |-
| |
| |align = "right"|''' Bremsweg (in m)'''
| |
| |align = "right"|<font size = "3">1</font>
| |
| |align = "right"|<font size = "3">4</font>
| |
| |align = "right"|<font size = "3">9</font>
| |
| |align = "right"|<font size = "3">16</font>
| |
| |align = "right"|<font size = "3">25</font>
| |
| |align = "right"|<font size = "3">64</font>
| |
| |align = "right"|<font size = "3">100</font>
| |
| |align = "right"|<font size = "3">144</font>
| |
| | |
| |}
| |
| | |
|
| |
| | |
| {{Arbeit|
| |
| ARBEIT=
| |
| a) Stelle die Daten aus der Tabelle in einem Koordinatensystem dar.
| |
| | |
| b) Verbinde die Punkte zu einem Funktionsgraphen (der keine Ecken haben sollte.)
| |
| | |
| c) Ermittle anhand des Graphen einen Schätzwert für den Bremsweg bei 70 km/h.
| |
| | |
|
| |
| | |
| : '''Lösung:''' {{versteckt|<ggb_applet height="400" width="600" showResetIcon="true" filename="bremsweg01.ggb" />}}
| |
| }}
| |
| | |
| == Der Funktionsterm ==
| |
| | |
| [Hier muss noch ein Text hin, der die Schüler zur Formel s=0,01*v^2 führt.]
| |
| | |
| {{Arbeit|
| |
| ARBEIT=
| |
| a) Hinter den Daten der Wertetabelle steckt ein Muster.
| |
| Versuche eine Formel zu finden, mit deren Hilfe man aus der Geschwindigkeit den Bremsweg berechnen kann.
| |
| | |
| b) In der Fahrschule lernt man: BW = v/10 mal v/10 (Bremsweg = Geschwindigkeit durch 10 mal Geschwindigkeit durch 10).<br />
| |
| Vergleiche diese Formel mit der von dir in a) gefundenen Formel.
| |
| }}
| |
| | |
| == Unfallprotokoll ==
| |
| | |
| Arbeiten mit dem Funktionsterm und dem Graphen (Geschwindigkeit → Bremsweg und Bremsweg → Geschwindigkeit)
| |
| | |
| -> Unfallprotokoll der Polizei
| |
| | |
| | |
| == Unterschiedliche Straßenverhältnisse ==
| |
| | |
| Unterschiedliche Straßenverhältnisse, dadurch Variation von a [GeoGebra]
| |
| | |
| :Wie muss a gewählt werden, damit bei der Geschwindigkeit von 74 km/h der Bremsweg 65 m lang ist?
| |
| | |
|
| |
|
| Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form Zahl mal Variable im Quadrat. Sie zählen daher zu den '''quadratischen Funktionen'''. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen (welches ja bekanntlich Geraden sind).
| | | |
| | ==== Für die Lehrerinnen und Lehrer ==== |
| | {{pdf|Didaktischer_Kommentar_quad_Fkt.pdf|Didaktischer Kommentar}} |
|
| |
|
| {{Merksatz|MERK= Die Graphen von Funktionen mit der Funktionsgleichung f(x)=ax² heißen Parabeln.
| |
|
| |
| Für a>0 gilt: Je größer a ist, desto steiler ist die Parabel.}}
| |
|
| |
| == Der Anhalteweg ==
| |
|
| |
| Wir haben oben gesehen, dass man selbst bei relativ moderaten Geschwindigkeiten mit beachtlichen Bremswegen rechnen muss. Dabei blieb jedoch noch unberücksichtigt, dass der ''Anhalteweg'' nicht allein der reine ''Bremsweg'' ist, sondern dass zum Bremsweg auch noch der sogenannte ''Reaktionsweg'' hinzukommt.<br />
| |
| Der Bremsweg ist derjenige Weg, den das Fahrzeug vom Beginn des Bremsvorgangs bis zum Stillstand zurücklegt. Er berücksichtigt also nicht, dass man nach dem Auftreten des Hindernisses eine gewisse Zeit (die ''Reaktionszeit'') benötigt, bis man überhaupt reagieren kann und bremst. Der Weg, den das Fahrzeug angesichts der Reaktionszeit noch ungebremst zurücklegt, nennt man Reaktionsweg.
| |
|
| |
|
| |
| {{Arbeit|
| |
| ARBEIT=
| |
| a) Man kann davon ausgehen, dass die Reaktionszeit bei einem gewöhnlichen Autofahrer nicht länger ist als eine Sekunde. Berechne den Reaktionsweg, der sich bei einer Geschwindigkeit von <br />
| |
| : (1) 30 km/h, (2) 50 km/h, (3) 100 km/h<br />
| |
| aus einer Reaktionszeit von einer Sekunde ergibt.<br />
| |
| b) Ermittle eine Formel, mit Hilfe derer man den Reaktionsweg aus der Geschwindigkeit berechnen kann. Geh dabei wieder von einer Reaktionszeit von einer Sekunde aus.<br />
| |
| c) Ermittle eine möglichst einfache Formel, mit Hilfe derer man den Anhalteweg aus der Geschwindigkeit berechnen kann.<br />
| |
| d) In der Fahrschule lernt man folgende Formeln:<br />
| |
| :Reaktionsweg = Geschwindigkeit durch 10 mal drei<br />
| |
| :Bremsweg = Geschwindigkeit durch 10 mal Geschwindigkeit durch 10<br />
| |
| :Anhalteweg = Reaktionsweg + Bremsweg<br />
| |
| Vergleiche die Fahrschulformeln mit deinen bisherigen Ergebnissen.}}
| |
|
| |
| == Unterschiedliche Straßenverhältnisse ==
| |
|
| |
| Im folgenden Applet ist der Zusammenhang zwischen Geschwindigkeit und Anhalteweg ''für unterschiedliche Witterungsbedingungen'' dargestellt worden. Es ist ja klar, dass der Bremweg bei nasser Fahrbahn länger ist als bei trockener. <br />
| |
| Du kannst [...] Schieberegler [...]
| |
|
| |
| : [Hier muss noch ein GeoGebra-Applet eingefügt werden.]
| |
|
| |
| {{Arbeit|
| |
| ARBEIT=
| |
| a) [...] intuitiv am Graphen arbeiten<br />
| |
| b) Bei welchem Wert für a ist der Anhalteweg bei einer Geschwindigkeit von 60 km/h ungefähr 83 m lang?
| |
| }} | | }} |
| | </div> |
|
| |
|
| = Interaktive Übungen =
| |
|
| |
|
| Liebe Gabi, könntest du diesen Teil übernehmen?
| | {{Fortsetzung|weiter=Los geht's!|weiterlink=/Bremsweg}} |
|
| |
|
| = Arbeitsblätter und Links =
| | {{Autoren|Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann}} |
| == Arbeitsblätter ==
| |
| *[http://www.sinus.lernnetz.de/aufgaben1/materialien/mathematik/sek_I/quadratische_funktionen.doc Arbeitsblatt aus dem Sinus-Lernnetz]
| |
| | |
| == Links ==
| |
| *Ideen zum Thema [[Quadratische_Funktion/Wurfparabel|"Wurfparabel"]]
| |
| *[http://wiki.zum.de/Quadratische_Funktion Allgemeines zu Quadratischen Funktionen]
| |
| *{{wpde|Bremsweg|Bremsweg bei Wikipedia}}
| |
| | |
| | |
| {{Information| | |
| TITEL= Allgemeine Übungen|
| |
| INFO= Term -> Graph - Graph -> Term [Geogebra-Schieberegler] - Nullstellen - Scheitel
| |
| }} | |
|
| |
|
|
| | __NOTOC__ __NOEDITSECTION__ |
|
| |
|
| {{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]] und Gabi Jauck}}
| | [[Kategorie:Mathematik-digital]] |
| | [[Kategorie:Mathematik]] |
| | [[Kategorie:Lernpfad]] |
| | [[Kategorie:Sekundarstufe 1]] |
| | [[Kategorie:Analysis]] |