Nachricht für neue Nutzer.

Nachricht für engagierte Nutzer.

Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Karl Kirst
K (Karl Kirst verschob Seite Lernpfad: Lineare Funktionen/Station 2/Übung nach Lineare Funktionen/Station 2/Übung: ist ja bei Mathematik-digital auf jeden Fall ein Lernpfad)
 
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(40 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Lernpfad Lineare Funktionen}}
{{Navigation verstecken|{{Lernpfad Lineare Funktionen}}}}


<div class="grid">
<div class="width-1-6">[[Datei:Power-sports-1015688 1920.jpg|Bankdrücken]]</div>
<div class="width-5-6">


<div style="  width: 80%; border: 2px solid #c6d745; background-color:#c6d745; padding:7px;font-size:1px; height:1px; border-bottom:1px solid #c6d745;"></div>
<div style="  width: 80%; border: 2px solid #c6d745; background-color:#ffffff; align:center; padding:7px;">


'''Übung macht den Meister!''' In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß!</div>
</div>


==Übungen zur Station 2==
{|


|align = "left" width="260"|[[Datei:Power-sports-1015688 1920.jpg|200px|Bankdrücken]]
{{Box|5. Wie war das jetzt nochmal?|Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.|Üben}}
|align = "left" |'''Übung macht den Meister!''' In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß!
<center>[[Datei:Steigungsdreieck A1.png|300px|Bild zur Aufgabe 1]]</center>
|}
<br>
 
{| border="2" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#8E8CF2}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}};background-color: {{{Hintergrund|#ffffff}}}"
|-
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">[[Bild:Hand.gif|30px]]  
&nbsp; Übung 5: Wie war das jetzt nochmal?
</div>


<div class="lueckentext-quiz">
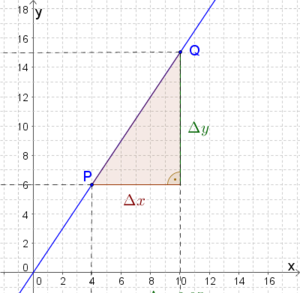
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.


Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.<br><br>
<math>m=\Delta</math>'''y''' <math>:\Delta </math> '''x''' = ('''y<sub>Q</sub>'''<math>-</math>'''y<sub>P</sub>''')<math>:</math>('''x<sub>Q</sub>'''<math>-</math>'''x<sub>P</sub>''')<math>=</math>('''15'''<math>-</math>'''6''')<math>:</math>('''10'''<math>-</math>'''4''')<math>=</math>'''1,5'''
[[Datei:Steigungsdreieck A1.png|300px|Bild zur Aufgabe 1]]


<div class="lueckentext-quiz">
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.<br><br>
<math>m=\Delta</math>'''y''' <math>:\Delta </math> '''x''' = ('''y<sub>Q</sub>'''<math>-</math>'''y<sub>P</sub>''')<math>:</math>('''x<sub>Q</sub>'''<math>-</math>'''x<sub>P</sub>''')<math>=</math>('''15'''<math>-</math>'''6''')<math>:</math>('''10'''<math>-</math>'''4''')<math>=</math>'''1,5'''<br>
<br>
Die Steigung der dargestellten Geraden ist <math>m=</math>'''1,5'''
Die Steigung der dargestellten Geraden ist <math>m=</math>'''1,5'''
</div>  
</div>  
|}


<br>
<br>


{{Box|6. Wie groß ist die Steigung?|
[[Datei:Lernpfad lineare Funktionen Station 2 Übung 6.png|right|500px|Graphen linearer Funktionen]]
Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.
* Notiere dein Rechnungen und Überlegungen im Übungsheft.
* Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
|Üben}}
{{Lösung versteckt|1=Die lilafarbene Gerade gehört zu einer proportionalen Funktion, da sie durch den Ursprung verläuft.
Ihre Steigung ist <math>m=\frac{1}{3}</math>.


Zur Berechnung der Steigung kann man z.B. die Punkte <math>O(0 | 0)</math> und <math>A(3 | 1)</math> verwenden.
}}


{| border="1" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#8E8CF2}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}};background-color: {{{Hintergrund|#ffffff}}}"
|-
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">[[Bild:Hand.gif|30px]]
&nbsp; Übung 6: Wie groß ist die Steigung?
</div>
{|
|! style="width:36%"|[[Datei:Browse-1019848 1920.jpg|220px|Buch lesen]]
|Schlage bitte dein Mathebuch auf der '''Seite 47''' auf und betrachte in '''Aufgabe 5''' diejenige Gerade, die zu einer proportionalen Funktion passt. Berechne von dieser einen Geraden die Steigung.<br>
*Notiere dein Rechnungen und Überlegung im Übungsheft.
*Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.<br>
<popup name="Lösung">
{|
<!-->|! style="width:50%"|<span style="color:darkgreen">grüne Gerade: <math>m=\frac{2}{3}</math> </span><br><br><!-->
|<span style="color:blue">blaue Gerade: <math>m=\frac{2}{3}</math> </span><br><br>
<!-->
|-
|<span style="color:black">schwarze Gerade: <math>m=-2,5</math> </span><br><br>
|<span style="color:red">rote Gerade: <math>m=1,25</math> </span><br>
|-
|<span style="color:orange">gelbe Gerade: <math>m=-1</math> </span><br>
|<span style="color:pink">lila Gerade: <math>m=-0,125</math> </span><br>
|}
<!-->
</popup>
|}
|}
<br>


{| border="1" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#8E8CF2}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}};background-color: {{{Hintergrund|#ffffff}}}"
{{Box|7. Zeichne die Gerade!|
|-
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">[[Bild:Hand.gif|30px]]
&nbsp; Übung 7: Zeichne die Gerade!
</div>
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
<br><br>
{|
|- style="align:left;vertical-align:bottom"
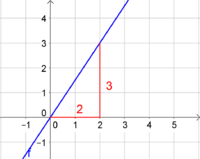
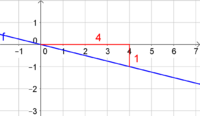
|! style="width:65% "| a) <math>f(x)=1,5\cdot x</math><br><br>b) <math>g(x)=-\frac{1}{4}\cdot x</math>
|<popup name = "Tipp zur a)">Wandle zunächst die Steigung 1,5 in einen Bruch um!</popup><br>
<popup name="Lösung">
{|
|a) [[Datei:Gerade zeichnen 1.png|200px|Steigung 1,5]]
|b) [[Datei:Gerade zeichnen 2.png|200px|Steigung 1,5]]
|}
</popup>
|}
|}
<br>
<br>
----
----


<!-->
a) <math>f(x)=1,5\cdot x</math>
==Doping für Schnelle==
<span style ="color:blue">Du liegst '''gut in der Zeit?'''</span> [[File:Animated winking Smiley colored.gif|100px|right|Animated winking Smiley colored]]
Dann versuch doch, den armen Radfahrern zu helfen...!


{| border="1" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#8E8CF2}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}};background-color: {{{Hintergrund|#ffffff}}}"
b) <math>g(x)=-\frac{1}{4}\cdot x</math>
|-
|Üben}}
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">[[Bild:Hand.gif|30px]]  
{{Lösung versteckt|Wandle zunächst die Steigung 1,5 in einen Bruch um!|Tipp zu a)|Verbergen}}
&nbsp; Für Schnelle - Übung 8: Tour de France!
{{Lösung versteckt|a) [[Datei:Gerade zeichnen 1.png|200px|Steigung 1,5]]
</div>
b) [[Datei:Gerade zeichnen 2.png|200px|Steigung 1,5]]}}
{|
|Damit die Radfahrer wissen, wie viel Doping sie zur Tour de France mitnehmen sollen, müssen sie wissen, welche Steigungen im Mittel zu erwarten sind.<br>
Bearbeite dazu die im Übungsheft '''Aufgabe 6 auf Seite 34.'''<br><br>
{|
|style="width:40%"|Du weißt nicht wie du anfangen sollst?<br>
<popup name="Tipp 1">
"mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft ''gleichmäßig'' zwischen zwei Punkten.
Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden...
</popup><br>


<popup name="Tipp 2">
Wenn du die Punkte mit je einer Geraden verbunden hast, musst du Steigungsdreiecke einzeichnen und damit die Steigung bestimmen.
</popup><br>
|
| width="260"|<popup name="Lösung der Aufgabe">
Legt man den Koordinatenusrprung in den Punkt A so gilt:<br>
[[Datei:Bergsteigung Lsg.png|500px|mittlere Steigungen]]
</popup><br>
|}
{{Frage|
Musst du alle Längen aus der Zeichnung, die zur Bestimmung der Steigung nötig sind, erst in die realen Längen umrechnen?
}}
|style="align:left;vertical-align:top"|[[Datei:Berg Steigung.png|280px|Berg Steigung]]
|}


|}


<!-->


</div>
<br>
----
'''Alles geschafft? Super, dann auf zu Station 3!'''
'''Alles geschafft? Super, dann auf zu Station 3!'''
{|border="0" cellspacing="0" cellpadding="4"
|align = "left" width="60"|[[Datei:binoculars-1015267_1920.jpg|150px]]
|align = "left"|[[../../Station_3|'''...hier geht es weiter''']]'''!'''


|}
{{Fortsetzung|weiter=Station 3|weiterlink=../../Station_3}}
 


{{Lernpfad Lineare Funktionen}}
[[Kategorie:Funktionen]]
[[Kategorie:Lineare Funktion]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:R-Quiz]]

Aktuelle Version vom 4. Januar 2025, 16:22 Uhr

Bankdrücken


Übung macht den Meister! In dieser Station kannst du dein eben erworbenes oder vertieftes Wissen festigen. Viel Spaß!


5. Wie war das jetzt nochmal?
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
Bild zur Aufgabe 1

Die Steigung m berechnet man mithilfe des Steigungsdreiecks.

= ()()()()

Die Steigung der dargestellten Geraden ist

yQ10xQyPxPyx1,56151,54


6. Wie groß ist die Steigung?
Graphen linearer Funktionen

Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.

  • Notiere dein Rechnungen und Überlegungen im Übungsheft.
  • Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.


7. Zeichne die Gerade!

Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!

a)

b)



Alles geschafft? Super, dann auf zu Station 3!

Station 3
Abgerufen von „https://unterrichten.zum.de/index.php?title=Lineare_Funktionen/Station_2/Übung&oldid=139273“