Exkurs zur Normalverteilung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<center>[[Bild: Bin2.gif]]</center> | <center>[[Bild: Bin2.gif]]</center> | ||
{{Aufgaben | {{Aufgaben|1=1|2= | ||
1. Blende die phi-Funktion ein und beschreibe wie sich ihr Graph verändert, wenn man n verändert. | |||
2. Für welche wähle n<10. Für welche Werte von p ist die phi-Funktion eine gute/schlechte Näherung. | |||
3. Wähle n>500. Was gilt nun? | |||
4. Diskutiere die phi-Funktion durch Rechnung und mit den Mitteln, die Geogebra zur Verfügung stellt.(Maximum, Wendepunkte, Krümmungsverhalten) | |||
4. Diskutiere die phi-Funktion durch Rechnung und mit den Mitteln, die Geogebra zur Verfügung stellt.(Maximum, Wendepunkte, Krümmungsverhalten) | |||
5. Bei sehr großem Wert von n ist also die Wahrscheinlichkeit F(n,p,r) in etwa gleich dem Flächeninhalt unter der Kurve phi. Diesen wollen wir mit Phi(x) bezeichnen. Wie kann man diesen bestimmen? Schreibe einen möglichen Ansatz auf. | 5. Bei sehr großem Wert von n ist also die Wahrscheinlichkeit F(n,p,r) in etwa gleich dem Flächeninhalt unter der Kurve phi. Diesen wollen wir mit Phi(x) bezeichnen. Wie kann man diesen bestimmen? Schreibe einen möglichen Ansatz auf. | ||
6. Bestimme mittels Geogebra und der phi-/Phi-Funktion die Wahrscheinlichkeit, dass bei 6000 Würfen mit einem Würfel ein Sechser mindestens 750 Mal, aber höchstens 1250 Mal auftritt. Vergleiche die Wahrscheinlichkeit, wenn Du die Binomialverteilung nimmst. | 6. Bestimme mittels Geogebra und der phi-/Phi-Funktion die Wahrscheinlichkeit, dass bei 6000 Würfen mit einem Würfel ein Sechser mindestens 750 Mal, aber höchstens 1250 Mal auftritt. Vergleiche die Wahrscheinlichkeit, wenn Du die Binomialverteilung nimmst. | ||
}} | |||
Das Dilemma ist nun zum einen, dass man diese Funktion Phi(n,p,r) nicht geschlossen darstellen kann. Zum anderen hat man gesehen, dass die phi-Funktionen von n und p abhängig sind. Das Tafelwerk müsste extrem umfangreich sein. | Das Dilemma ist nun zum einen, dass man diese Funktion Phi(n,p,r) nicht geschlossen darstellen kann. Zum anderen hat man gesehen, dass die phi-Funktionen von n und p abhängig sind. Das Tafelwerk müsste extrem umfangreich sein. | ||
| Zeile 41: | Zeile 27: | ||
'''unabhängig von n oder p''' und für diese lässt sich der Integralwert in Stochastischen Tafelsammlungen leicht [http://www.vwi.tu-dresden.de/~treiber/statistikFormelnTabellen/erf_tab.pdf tabellieren]. | '''unabhängig von n oder p''' und für diese lässt sich der Integralwert in Stochastischen Tafelsammlungen leicht [http://www.vwi.tu-dresden.de/~treiber/statistikFormelnTabellen/erf_tab.pdf tabellieren]. | ||
<center> [[Bild:Bin5.gif]] | <center> [[Bild:Bin5.gif]] [[Bild:Heim24.gif|frame|Ansicht der GEOGEBRA-Anwendung]]</center> | ||
Mit der folgenden Anwendung kann man ebenfalls ohne Verwendung einer Tabelle Aufgaben lösen, für die man konventionell nicht mit der Binomialverteilung arbeiten konnte, sondern auf die Normalverteilung mit Tafelwerk angewiesen war. In Geogebra sind die Aufgaben sowohl mit der obigen Anwendung möglich als auch mit der unten angegebenen. | |||
<ggb_applet id="EQXbEn8f" width="900" height="552"/> | |||
<ggb_applet | |||
== Ein Beispiel für ganz andere Verteilungen == | == Ein Beispiel für ganz andere Verteilungen == | ||
Das delta 12 auf S. 113/20 beschreibt eine Anwendung aus der Wirtschaft, die für die Abschätzung von Garantiefragen wichtig ist. | Das delta 12 auf S. 113/20 beschreibt eine Anwendung aus der Wirtschaft, die für die Abschätzung von Garantiefragen wichtig ist. | ||
Simulieren lässt sich dies durch die folgende Geogebra-Anwendung: | Simulieren lässt sich dies durch die folgende Geogebra-Anwendung: | ||
<center>[[Bild:Heim26.gif]]</center> | |||
<center> | |||
<ggb_applet height="450" width="600" filename="garantie.ggb" /> | |||
<ggb_applet height="450" width="600" filename="garantie. | |||
<br><br> | <br><br> | ||
| Zeile 89: | Zeile 47: | ||
*[http://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm Rechner für Normal- Bionomial- und Poissonverteilung] | *[http://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm Rechner für Normal- Bionomial- und Poissonverteilung] | ||
Aktuelle Version vom 10. November 2018, 21:45 Uhr
Exkurs zur Normalverteilung 1
Wir betrachten folgende Funktion. Sie ist in unserem "Experimentierkasten" bereits definiert
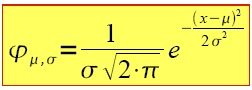
1. Blende die phi-Funktion ein und beschreibe wie sich ihr Graph verändert, wenn man n verändert. 2. Für welche wähle n<10. Für welche Werte von p ist die phi-Funktion eine gute/schlechte Näherung. 3. Wähle n>500. Was gilt nun?
4. Diskutiere die phi-Funktion durch Rechnung und mit den Mitteln, die Geogebra zur Verfügung stellt.(Maximum, Wendepunkte, Krümmungsverhalten)
5. Bei sehr großem Wert von n ist also die Wahrscheinlichkeit F(n,p,r) in etwa gleich dem Flächeninhalt unter der Kurve phi. Diesen wollen wir mit Phi(x) bezeichnen. Wie kann man diesen bestimmen? Schreibe einen möglichen Ansatz auf.
6. Bestimme mittels Geogebra und der phi-/Phi-Funktion die Wahrscheinlichkeit, dass bei 6000 Würfen mit einem Würfel ein Sechser mindestens 750 Mal, aber höchstens 1250 Mal auftritt. Vergleiche die Wahrscheinlichkeit, wenn Du die Binomialverteilung nimmst.
Das Dilemma ist nun zum einen, dass man diese Funktion Phi(n,p,r) nicht geschlossen darstellen kann. Zum anderen hat man gesehen, dass die phi-Funktionen von n und p abhängig sind. Das Tafelwerk müsste extrem umfangreich sein.
Exkurs zur Normalverteilung 2
Die Koordinatentransformation

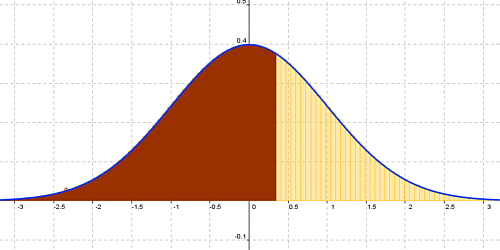
verschiebt die Histogramme mit ihrem Erwartungswert in den Ursprung und staucht sie in x-Richtung um den Faktor sigma, streckt sie in y-Richtung auf das sigma-fache: der Flächeninhalt des Rechtecks, das B(n,p,r) bleibt also gleich.
Die Funktion phi, die für jedes n und jedes p eine andere Kurve lieferte geht über in eine einzige Funktion:
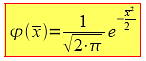
unabhängig von n oder p und für diese lässt sich der Integralwert in Stochastischen Tafelsammlungen leicht tabellieren.
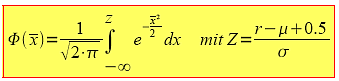
Mit der folgenden Anwendung kann man ebenfalls ohne Verwendung einer Tabelle Aufgaben lösen, für die man konventionell nicht mit der Binomialverteilung arbeiten konnte, sondern auf die Normalverteilung mit Tafelwerk angewiesen war. In Geogebra sind die Aufgaben sowohl mit der obigen Anwendung möglich als auch mit der unten angegebenen.

Ein Beispiel für ganz andere Verteilungen
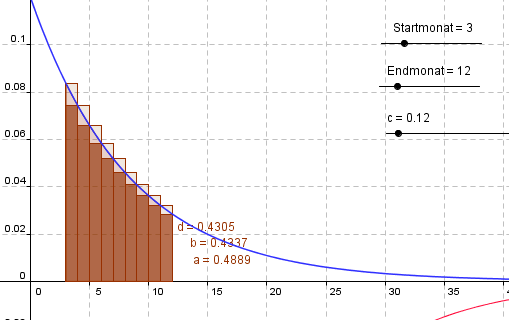
Das delta 12 auf S. 113/20 beschreibt eine Anwendung aus der Wirtschaft, die für die Abschätzung von Garantiefragen wichtig ist.
Simulieren lässt sich dies durch die folgende Geogebra-Anwendung:
Die Datei [INVALID] wurde nicht gefunden.