Elementarteilchen und Radioaktiver Zerfall/Zerfallsgesetz: Unterschied zwischen den Versionen
Mono13 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Mono13 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
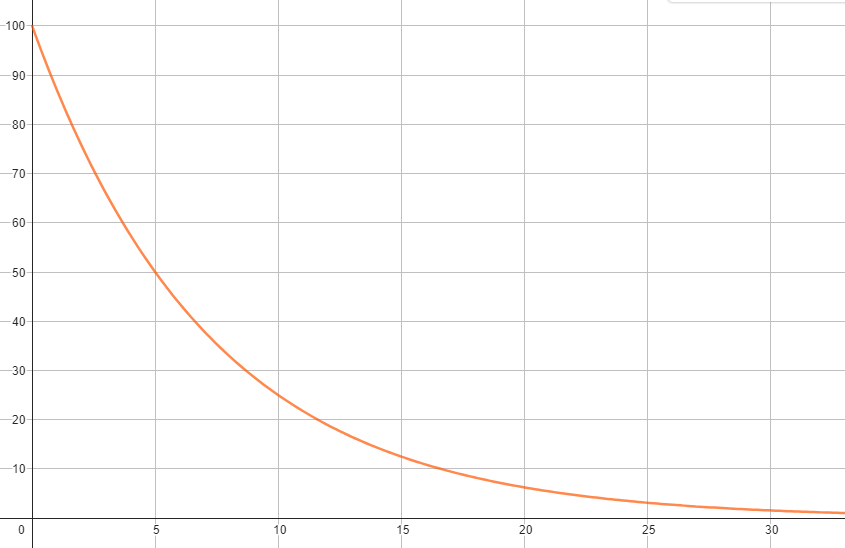
Wenn man sich den Graphen anschaut, dann sieht man, dass sich die Menge radioaktiver Atomkerne nach einer Halbwertszeit immer '''halbiert'''. Wenn ich also einen Term aufstellen möchte, mit dem ich die Menge radioaktiver Kerne nach einer Halbwertszeit berechnen kann, dann muss ich die Anfangsmenge radioaktiver Kerne mit '''0,5''' multiplizieren. Wenn ich die Anfangsmenge radioaktiver Kerne | Wenn man sich den Graphen anschaut, dann sieht man, dass sich die Menge radioaktiver Atomkerne nach einer Halbwertszeit immer '''halbiert'''. Wenn ich also einen Term aufstellen möchte, mit dem ich die Menge radioaktiver Kerne nach einer Halbwertszeit berechnen kann, dann muss ich die Anfangsmenge radioaktiver Kerne mit '''0,5''' multiplizieren. Wenn ich die Anfangsmenge radioaktiver Kerne N<sub>0</sub> nenne, dann wäre der Term also '''N<sub>0</sub> ⋅ 0,5'''. | ||
Wie wäre das denn, wenn ich die Menge radioaktiver Kerne nach zwei Halbwertszeiten berechnen möchte? Sie würde sich dann ja ein zweites Mal '''halbieren'''. Insgesamt ist von der Anfangsmenge also noch '''ein Viertel''' über. Der Term zur Berechnung der Menge radioaktiver Kerne nach zwei Halbwertszeiten lautet dann also ''' | Wie wäre das denn, wenn ich die Menge radioaktiver Kerne nach zwei Halbwertszeiten berechnen möchte? Sie würde sich dann ja ein zweites Mal '''halbieren'''. Insgesamt ist von der Anfangsmenge also noch '''ein Viertel''' über. Der Term zur Berechnung der Menge radioaktiver Kerne nach zwei Halbwertszeiten lautet dann also '''N<sub>0</sub> ⋅ 0,5²'''. | ||
Ein Term für die Menge übriger radioaktiver Atomkerne nach 3 Halbwertszeiten würde dementsprechend ja ''' | Ein Term für die Menge übriger radioaktiver Atomkerne nach 3 Halbwertszeiten würde dementsprechend ja '''N<sub>0</sub> ⋅ 0,5³''' lauten. | ||
Und einer für die Menge nach 4 Halbwertszeiten ''' | Und einer für die Menge nach 4 Halbwertszeiten '''N<sub>0</sub> ⋅ 0,5<sup>4</sup>'''. | ||
Eigentlich multipliziere ich jedes Mal die Anfangsmenge | Eigentlich multipliziere ich jedes Mal die Anfangsmenge N<sub>0</sub> mit einer Potenz von '''0,5'''. Weil sich jedes Mal ändert, welche Potenz ich verwende, sollte ich für den Exponenten eine Variable verwenden. Die Variable steht dann für die Anzahl vergangener '''Halbwertszeiten'''. Wie sieht dann der Term aus? | ||
</div>. | </div>. | ||
{{Box | {{Box | ||
|Aufgaben 8.2: Finden eines allgemeinen Zerfallsterms | |Aufgaben 8.2: Finden eines allgemeinen Zerfallsterms | ||
|a) Stelle den gesuchten Term auf. | |a) '''Stelle den gesuchten Term auf'''. | ||
b) Überprüfe den Term an zwei Werten, die du dem Graphen entnimmst. | |||
b) '''Überprüfe''' den Term an zwei Werten, die du dem Graphen entnimmst. | |||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
Damit man für die Variable nicht die Anzahl vergangener Halbwertszeiten einsetzen muss, sondern die tatsächlich vergangene Zeit, teilt man die Variable im Exponenten durch die Halbwertszeit. Wenn zum Beispiel die Halbwertszeit 5 Jahre beträgt und 10 Jahre vergangen sind, dann hat man im Exponenten 10 Jahre : 5 Jahre = 2 stehen, was wieder der Anzahl vergangener Halbwertszeiten entspricht. | |||
Eine Gleichung zur Berechnung der Anzahl der übrigen Atomkerne nach einer bestimmten Zeit (N<sub>t</sub>) lautet also N<sub>t</sub> = __________. | |||
{{Box | |||
|Aufgaben 8.3: Plutonium-239 ist ein Alphastrahler und hat eine Halbwertszeit von 24000 Jahren. Nach dem Reaktorunglück in Tschernobyl sind große Mengen dieses Isotops in der Umgebung des Reaktors zurückgeblieben. | |||
|a) Ein Präparat Plutonium-239 enthält 500000 Atomkerne. Wie viele sind davon nach 100 Jahren noch vorhanden? | |||
b) Berechne die durchschnittliche Aktivität in den ersten 100 Jahren. | |||
c) Berechne, wie lang man warten muss, bis weniger als 5% der ursprünglichen Atomkerne vorhanden sind. | |||
Bewerte die zukünftige Bewohnbarkeit dieses Gebiets vor diesem Hintergrund. | |||
}} | |||
== Lerneinheiten == | |||
== Lerneinheiten == | == Lerneinheiten == | ||
[[Der Aufbau eines Atoms]] | 1. [[Der Aufbau eines Atoms]] | ||
[[Kennzahlen von Atomkernen]] | 2. [[Kennzahlen von Atomkernen]] | ||
[[Radioaktivität]] | 3. [[Radioaktivität]] | ||
[[Nachweis von Radioaktivität]] | 4. [[Nachweis von Radioaktivität]] | ||
[[Verschiedene Arten von Strahlung]] | 5. [[Verschiedene Arten von Strahlung]] | ||
[[Aktivität]] | 6. [[Aktivität]] | ||
[[Halbwertszeit]] | 7. [[Halbwertszeit]] | ||
[[Zerfallsgesetz]] | 8. [[Zerfallsgesetz]] | ||
Aktuelle Version vom 3. Januar 2024, 18:38 Uhr
Wenn man sich den Graphen anschaut, dann sieht man, dass sich die Menge radioaktiver Atomkerne nach einer Halbwertszeit immer halbiert. Wenn ich also einen Term aufstellen möchte, mit dem ich die Menge radioaktiver Kerne nach einer Halbwertszeit berechnen kann, dann muss ich die Anfangsmenge radioaktiver Kerne mit 0,5 multiplizieren. Wenn ich die Anfangsmenge radioaktiver Kerne N0 nenne, dann wäre der Term also N0 ⋅ 0,5. Wie wäre das denn, wenn ich die Menge radioaktiver Kerne nach zwei Halbwertszeiten berechnen möchte? Sie würde sich dann ja ein zweites Mal halbieren. Insgesamt ist von der Anfangsmenge also noch ein Viertel über. Der Term zur Berechnung der Menge radioaktiver Kerne nach zwei Halbwertszeiten lautet dann also N0 ⋅ 0,5².
Ein Term für die Menge übriger radioaktiver Atomkerne nach 3 Halbwertszeiten würde dementsprechend ja N0 ⋅ 0,5³ lauten. Und einer für die Menge nach 4 Halbwertszeiten N0 ⋅ 0,54.
Eigentlich multipliziere ich jedes Mal die Anfangsmenge N0 mit einer Potenz von 0,5. Weil sich jedes Mal ändert, welche Potenz ich verwende, sollte ich für den Exponenten eine Variable verwenden. Die Variable steht dann für die Anzahl vergangener Halbwertszeiten. Wie sieht dann der Term aus?
.
a) Stelle den gesuchten Term auf.
b) Überprüfe den Term an zwei Werten, die du dem Graphen entnimmst.
Damit man für die Variable nicht die Anzahl vergangener Halbwertszeiten einsetzen muss, sondern die tatsächlich vergangene Zeit, teilt man die Variable im Exponenten durch die Halbwertszeit. Wenn zum Beispiel die Halbwertszeit 5 Jahre beträgt und 10 Jahre vergangen sind, dann hat man im Exponenten 10 Jahre : 5 Jahre = 2 stehen, was wieder der Anzahl vergangener Halbwertszeiten entspricht.
Eine Gleichung zur Berechnung der Anzahl der übrigen Atomkerne nach einer bestimmten Zeit (Nt) lautet also Nt = __________.
a) Ein Präparat Plutonium-239 enthält 500000 Atomkerne. Wie viele sind davon nach 100 Jahren noch vorhanden?
b) Berechne die durchschnittliche Aktivität in den ersten 100 Jahren.
c) Berechne, wie lang man warten muss, bis weniger als 5% der ursprünglichen Atomkerne vorhanden sind. Bewerte die zukünftige Bewohnbarkeit dieses Gebiets vor diesem Hintergrund.
Lerneinheiten
Lerneinheiten
4. Nachweis von Radioaktivität
5. Verschiedene Arten von Strahlung
6. Aktivität