Umfang von Rechteck und Quadrat: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(43 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Box|1=Lernpfad|2= Umfang von Rechteck und Quadrat
|3=Lernpfad}}
{{Lernpfad-Navigation|
{{Lernpfad-Navigation|


Zeile 15: Zeile 10:
{{Box|Experimentieren|Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn bzw. deiner Nachbarin, wie du den Umfang eines Rechtecks berechnen kannst. https://www.geogebra.org/m/MhZVUNpe#material/q2fuqXUV  |Experimentieren}}
{{Box|Experimentieren|Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn bzw. deiner Nachbarin, wie du den Umfang eines Rechtecks berechnen kannst. https://www.geogebra.org/m/MhZVUNpe#material/q2fuqXUV  |Experimentieren}}


{{Box|Was ist ein Umfang?|Erkläre danach einem Schulkollegen bzw. einer Schulkollegin, was ein Umfang einer Figur ist. Haltet eure Ergebnisse hier fest: https://www.menti.com/aly62opm9o2c |Meinung}}
{{Box|Was ist ein Umfang?|Erkläre danach einem Schulkollegen bzw. einer Schulkollegin, was ein Umfang einer Figur ist. Holt euch bei der Lehrperson einen Zettel und haltet eure Ergebnisse dort fest. |Meinung}}


{{Box|Merke|Schreibe den folgenden Merksatz ins Geometrieheft (Überschrift: Umfang eines Rechtecks) |Merksatz}}
{{Box|Merke|Schreibe den folgenden Merksatz mit Beispiel ins Schulübungsheft (Überschrift: Umfang eines Rechtecks) |Merksatz}}
Den '''Umfang eines Rechtecks''' kannst du mit folgenden Formeln berechnen:  
Den '''Umfang eines Rechtecks''' kannst du mit folgenden Formeln berechnen:  


* <math>u = a + b + a + b</math>
* <math>u = a + b + a + b</math>
* <math>u = 2 \times a + 2 \times b </math>
* <math>u = 2 * a + 2 * b </math>
* <math>u = 2 \times (a + b)</math>
* <math>u = 2 * (a + b)</math>


Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.  
Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.  


[[Datei:Umfang Rechteck.png]]
[[Datei:Rechteck Umfang.png|1000px]]  


{{Box|Jetzt bist du an der Reihe!|Arbeitsmethode}}
{{Box|Jetzt bist du an der Reihe!||Arbeitsmethode}}  
Berechne den Umfang eines Rechtecks mit folgenden Angaben: a = 51 mm, b = 3 cm. Achte auf die Einheiten. Orientiere dich am Beispiel oben.
Berechne den Umfang eines Rechtecks mit folgenden Angaben: a = 51 mm, b = 3 cm. Achte auf die Einheiten. Orientiere dich am Beispiel oben.


{{Lösung versteckt|[[Datei:Rechteck Umfang 2.png|1000px]]|Lösung|Lösung}}


{{Box|Experimentieren|Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn, wie du den Umfang eines Quadrats berechnen kannst. https://www.geogebra.org/m/Bh9Xb7KT  |Experimentieren}}
{{Box|Experimentieren|Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn, wie du den Umfang eines Quadrats berechnen kannst. https://www.geogebra.org/m/Bh9Xb7KT  |Experimentieren}}




{{Box|Merke|Schreibe den folgenden Merksatz ins Geometrieheft (Überschrift: Umfang eines Quadrats)|Merksatz}}
{{Box|Merke|Schreibe den folgenden Merksatz ins Schulübungsheft (Überschrift: Umfang eines Quadrats)|Merksatz}}
Den Umfang eines Quadrats kannst du mit folgenden Formeln berechnen. Welche Formel du zur Berechnung verwendet, ist  dir selbst überlassen.  
Den Umfang eines Quadrats kannst du mit folgenden Formeln berechnen. Welche Formel du zur Berechnung verwendet, ist  dir selbst überlassen.  


* <math>u = a + a + a + a</math>
* <math>u = a + a + a + a</math>
* <math>u = 4\times a</math>
* <math>u = 4 * a</math>
 
{{Box|Memory||Lösung}}


{{Box|Üben: Kreuzworträtsel|Löse das Kreuzworträtsel mithilfe der Formeln zur Berechnung des Umfangs eines Rechtecks und Quadrats. Schreibe die Zahlen aus z.B. 50 = fünfzig.|Üben}}
Welche Angaben gehören zu welchem Umfang? Löse mithilfe der Formeln zur Berechnung des Umfangs eines Rechtecks und Quadrats. Schreibe die Rechenschritte in dein Schulübungsheft. Überschrift: Memory.  
<div class="kreuzwort-quiz">
 
{|
<div class="memo-quiz" >
|-
{|  
| sechszig || Quadrat: a = 15, u = ?
| Quadrat: a = 15cm, u = ? || 60cm
|-
|-
| sechsundzwanzig || Rechteck: a = 6 , b = 7 , u = ?
| Rechteck: a = 6cm , b = 7cm , u = ?|| 26cm
|-
|-
| hundertsechsundneunzig || Quadrat: a = 49 , u = ?
| Quadrat: a = 49dm , u = ? || 196dm
|-
|-
| zehntausendeinundsechzig || Rechteck : a = 968 , b = ? , u = 22 058
| 10061cm  || Rechteck : a = 968cm , b = ? , u = 22 058cm
|-
|-
| vier || Quadrat: u = 16 , a = ?
| 4m || Quadrat: u = 16m , a = ?
|-
|-
|-
| 256cm || Rechteck: a = 70cm , b = 58cm , u = ?
| zweihundertsechsundfünzig || Rechteck: a = 70 , b = 58 , u = ??
|}
|}
</div>
</div>
{{Box|Üben|Textaufgaben. Versuche die Textaufgaben im Schulübungsheft zu lösen. Achte auf eine ordentliche Form und halte dich dabei an den Beispielen des Merktextes fest. |Üben}}
# Ein Hühnerstall soll einen neuen Zaun bekommen. Das Gehege ist 8 m lang und 5 m breit. Wie viel Meter Zaun müssen für das Gehege gekauft werden?
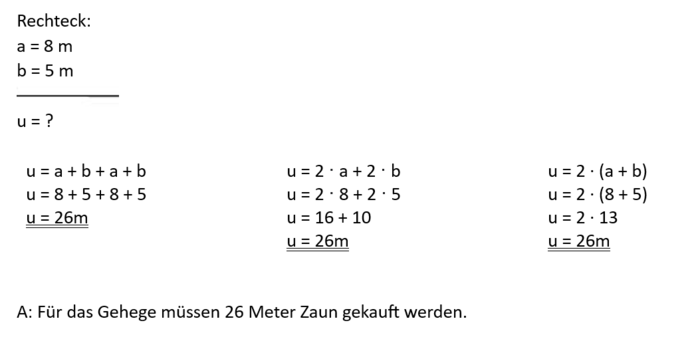
{{Lösung versteckt| [[Datei:Hühnerstall.png|700px]]|Lösung |Lösung}}
# Timo läuft dreimal um den quadratischen Spielplatz, der eine Seitenlänge von 27 m hat. Wie weit muss Timo laufen?
{{Lösung versteckt| A: Timo muss 324 Meter laufen. |Lösung |Lösung}}
{{Fortsetzung|weiter=Flächenberechnung von Rechteck und Quadrat|}}

Aktuelle Version vom 24. Mai 2023, 06:08 Uhr

  1. Aktivierung des Vorwissens und Eigenschaften von Rechteck und Quadrat
  2. Konstruktionen von Rechteck und Quadrat
  3. Umfang von Rechteck und Quadrat
  4. Flächenberechnung von Rechteck und Quadrat
  5. Expertenaufgaben für schnelle Rechenfüchse

Experimentieren
Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn bzw. deiner Nachbarin, wie du den Umfang eines Rechtecks berechnen kannst. https://www.geogebra.org/m/MhZVUNpe#material/q2fuqXUV

Was ist ein Umfang?
Erkläre danach einem Schulkollegen bzw. einer Schulkollegin, was ein Umfang einer Figur ist. Holt euch bei der Lehrperson einen Zettel und haltet eure Ergebnisse dort fest.

Merke
Schreibe den folgenden Merksatz mit Beispiel ins Schulübungsheft (Überschrift: Umfang eines Rechtecks)

Den Umfang eines Rechtecks kannst du mit folgenden Formeln berechnen:

Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.

Rechteck Umfang.png

Jetzt bist du an der Reihe!

Berechne den Umfang eines Rechtecks mit folgenden Angaben: a = 51 mm, b = 3 cm. Achte auf die Einheiten. Orientiere dich am Beispiel oben.

Rechteck Umfang 2.png

Experimentieren
Sieh dir die Geogebra - Datei an und diskutiere mit deinem Nachbarn, wie du den Umfang eines Quadrats berechnen kannst. https://www.geogebra.org/m/Bh9Xb7KT


Merke
Schreibe den folgenden Merksatz ins Schulübungsheft (Überschrift: Umfang eines Quadrats)

Den Umfang eines Quadrats kannst du mit folgenden Formeln berechnen. Welche Formel du zur Berechnung verwendet, ist dir selbst überlassen.

Memory

Welche Angaben gehören zu welchem Umfang? Löse mithilfe der Formeln zur Berechnung des Umfangs eines Rechtecks und Quadrats. Schreibe die Rechenschritte in dein Schulübungsheft. Überschrift: Memory.

Quadrat: a = 15cm, u = ? 60cm
Rechteck: a = 6cm , b = 7cm , u = ? 26cm
Quadrat: a = 49dm , u = ? 196dm
10061cm Rechteck : a = 968cm , b = ? , u = 22 058cm
4m Quadrat: u = 16m , a = ?
256cm Rechteck: a = 70cm , b = 58cm , u = ?


Üben
Textaufgaben. Versuche die Textaufgaben im Schulübungsheft zu lösen. Achte auf eine ordentliche Form und halte dich dabei an den Beispielen des Merktextes fest.
  1. Ein Hühnerstall soll einen neuen Zaun bekommen. Das Gehege ist 8 m lang und 5 m breit. Wie viel Meter Zaun müssen für das Gehege gekauft werden?
Hühnerstall.png
  1. Timo läuft dreimal um den quadratischen Spielplatz, der eine Seitenlänge von 27 m hat. Wie weit muss Timo laufen?
A: Timo muss 324 Meter laufen.
Flächenberechnung von Rechteck und Quadrat
Abgerufen von „https://unterrichten.zum.de/index.php?title=Umfang_von_Rechteck_und_Quadrat&oldid=135013“