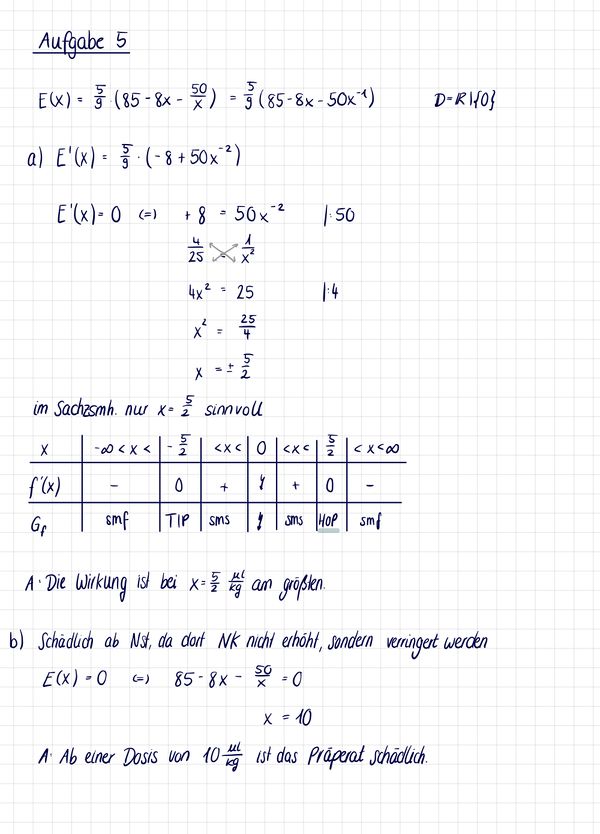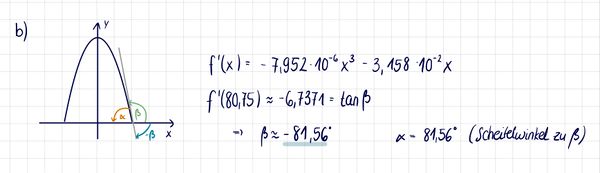Übungen Funktionsuntersuchung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (58 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==== | |||
<span class="brainy hdg-ruler-pencil fa-3x" "></span>Untersuche die Funktion auf Symmetrie. Bestimme die Schnittpunkte mit den Achsen, ggf. das Verhalten an den Definitionslücken, das Verhalten im Unendlichen und die Extrema. Skizziere anschließend | ====<span class="brainy hdg-ruler-pencil fa-3x" "></span>Aufgabe 1==== | ||
Untersuche die Funktion auf Symmetrie. Bestimme die Schnittpunkte mit den Achsen, ggf. das Verhalten an den Definitionslücken, das Verhalten im Unendlichen und die Extrema. Skizziere anschließend <math>G_f</math>. | |||
a) <math>f(x)= \frac{1}{2}x^3-4x^2+8x</math> | |||
b) <math>f(x)= \frac{4+x^2}{x^2-9}</math> | b) <math>f(x)= \frac{4+x^2}{x^2-9}</math> | ||
c) <math>f(x)= \frac{x^2-4}{x^2+1}</math> | c) <math>f(x)= \frac{1}{6}(x+1)^2(x-2)</math> <span class="brainy hdg-star fa-2x" "></span> | ||
d) <math>f(x)= \frac{x^2-4}{x^2+1}</math> <span class="brainy hdg-rocket fa-2x" "></span> | |||
e) <math>f(x)= 2-\frac{5}{2}x^2+x^4</math> <span class="brainy hdg-rocket fa-2x" "></span> | |||
{{Lösung versteckt|Überprüfe deine Ergebnisse eigenständig mithilfe von [https://www.geogebra.org/calculator GeoGebra] |Tipp anzeigen|Tipp verbergen}} | |||
{{Lösung versteckt|[[Datei:1c LSG.jpg|ohne|mini|834x834px]]|Lösung a) anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung b.jpg|ohne|mini|791x791px]]|Lösung b) anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt|[[Datei:1a LSG.jpg|ohne|mini|872x872px]]|Lösung c) anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung d.jpg|ohne|mini|600x600px]]|Lösung d) anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung e.jpg|ohne|mini|600x600px]]|Lösung e) anzeigen|Lösung verbergen}} | |||
====<span class="brainy hdg-ruler-pencil fa-3x" "></span>Aufgabe 2==== | |||
Untersuche die Funktion f soweit, dass du den Graphen skizzieren kannst. Bestimme anschließend graphisch und rechnerisch die [https://lernplattform.mebis.bayern.de/pluginfile.php/63262829/mod_resource/content/1/Tangentengleichung%20bestimmen.pdf Gleichung der Tangente] <span class="brainy hdg-magnifying-glass fa-1x" "> an den Graphen <math> G_f </math>, die parallel zur Gerade <math> g </math> verläuft und skizziere diese. | |||
a) <math>f(x)=-2x^2+12x-10</math>; <math>g(x)=-4x+6</math> | |||
b) <math>f(x)=x^3-6x^2+10x+4</math>; <math>g(x)=x+8</math><span class="brainy hdg-rocket fa-2x" "></span> | |||
{{Lösung versteckt|Zwei Geraden sind parallel, wenn sie die gleiche Steigung haben. |Tipp 1 anzeigen|Tipp 1 verbergen}} | |||
{{Lösung versteckt|Die Steigung der Tangenten in einem Punkt, entspricht der Steigung des Graphen, also der Ableitung, in diesem Punkt. |Tipp 2 anzeigen|Tipp 2 verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung 2a.jpg|ohne|mini|600x600px]]|Lösung a) anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung 2b.jpg|ohne|mini|600x600px]]|Lösung b) anzeigen|Lösung verbergen}} | |||
====<span class="brainy hdg-ruler-pencil fa-3x" "></span>Aufgabe 3<span class="brainy hdg-star fa-1x" "></span>==== | |||
Betrachtet werden die Funktionen | |||
<math>f_1(x)=x^3-x^2+3x</math> | |||
<math>f_1(x)=x^3-3x^2+3x</math> | |||
<math>f_1(x)=x^3-4x^2+3x</math> | |||
a) Stelle den Parameter a jeweils so ein, dass du <math>f_1, f_2</math> bzw. <math>f_3</math> erhältst. Vergleiche die Anzahl der Extrema der drei Funktionen. | |||
b) Alle drei Funktionsterme haben die Form <math>f_a(x)=x^3+ax^2+3x</math>. Für welche Parameterwerte <math>a \in \R </math> besitzen die Funktionen, die diese Form haben, zwei Extrema, einen Terrassenpunkt bzw. kein Extremum? Beweise deine Überlegungen auch rechnerisch. | |||
<span class="brainy hdg-lamp2 fa-2x" "></span> Falls dir das GeoGebra-Applet nicht richtig angezeigt wird, lade die Seite neu. | |||
{{Lösung versteckt|Überlege, wie sich die Anzahl der Extremstellen in der Ableitung widerspiegelt. |Tipp 1 anzeigen|Tipp 1 verbergen}} | |||
{{Lösung versteckt|Bestimme die Ableitung und deren Nullstellen in Abhängigkeit von a. Wähle a so, dass die Ableitung keine, eine bzw. zwei Nullstellen hat.|Tipp 2 anzeigen|Tipp 2 verbergen}} | |||
<ggb_applet id="f8cr4t7x" width="800" height="600"></ggb_applet> | |||
{{Lösung versteckt|[[Datei:Lösung 3.jpg|ohne|mini|600x600px]]|Lösung anzeigen|Lösung verbergen}} | |||
====<span class="brainy hdg-screen01 fa-3x" "></span>Aufgabe 4==== | |||
{{LearningApp | |||
| app = pwpensd1v22 | |||
| height = 500px | |||
}} | |||
====<span class="brainy hdg-ruler-pencil fa-3x" "></span>Aufgabe 5==== | |||
Seit Jahrtausenden wird die Mistel in der Heilbehandlung eingesetzt. In neuester Zeit wird der Mistelwirkstoff Lektin bei der Behandlung von Krebspatienten verwendet. Mistellektine steigern die Anzahl und die Aktivität der NK-Zellen (Natürliche Killerzellen, die direkt an der Tumorabwehr beteiligt sind): | |||
Die Erhöhung E der Aktivität der NK-Zellen (in %) durch Lektinpräparate hängt entscheidend von der Dosis x (in <math>\mu l</math> pro kg Körpergewicht) ab. Sie kann für <math> x\geq \frac{5}{8} </math> näherungsweise durch <math>E(x)=\frac{5}{9}(85-8x- \frac{50}{x}) </math> beschrieben werden. | |||
a) Bestimme die Dosis, bei welcher die Wirkung am größten ist. | |||
b) Bestimme die Dosis, ab welcher das Präparat sogar schädlich ist. | |||
{{Lösung versteckt|Verdeutliche dir den Graphen mithilfe von [https://www.geogebra.org/calculator GeoGebra] |Tipp anzeigen|Tipp verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung A5.jpg|ohne|mini|834x834px]]|Lösung anzeigen|Lösung verbergen}} | |||
====Aufgabe 6==== | |||
<span class="brainy hdg-ruler-pencil fa-3x" "></span>Der Innenbogen des "[https://de.wikipedia.org/wiki/Gateway_Arch_National_Park Gateway-Arch]" in St. Louis (USA) lässt sich näherungsweise durch die Funktion | |||
<math>f(x)=187,5-1,579 \cdot 10^{-2}x^2-1,998 \cdot 10^{-6}x^4</math> (x in m) beschreiben. | |||
a) Berechne die Höhe und die maximale Breite des Innenbogens. | |||
{{Lösung versteckt|Schaue dir die Funktion in GeoGebra an und mache dir klar, was der Höhe und der Breite des Bogens entspricht.|Tipp 1 anzeigen|Tipp 1 verbergen}} | |||
{{Lösung versteckt|Bestimme die Nullstellen durch [[Substitution]].|Tipp 2 anzeigen|Tipp 2 verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung 6a.jpg|ohne|mini|600x600px]]|Lösung a anzeigen|Lösung a verbergen}} | |||
b) Bestimme die Größe des Winkels zwischen dem Innenbogen und der Grundfläche. | |||
{{Lösung versteckt|Dieser Winkel entspricht dem [[Steigungswinkel]] der Tangente durch die Nullstelle.|Tipp anzeigen|Tipp verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung 6b.jpg|ohne|mini|600x600px]]|Lösung b anzeigen|Lösung b verbergen}} | |||
c) Bei einer Flugveranstaltung soll ein Flugzeug mit einer Flügelspannweite von 18m unter dem Bogen hindurchfließen. Welche Maximalflughöhe muss der Pilot einhalten, wenn in vertikaler und in horizontaler Richtung ein Sicherheitsabstand zum Bogen von 10m eingehalten werden muss? <span class="brainy hdg-rocket fa-1x" "></span><span class="brainy hdg-star fa-1x" "> | |||
{{Lösung versteckt| Verdeutliche dir den Sachverhalt an einer Skizze.|Tipp 3 anzeigen|Tipp 3 verbergen}} | |||
====<span class="brainy hdg-ruler-pencil fa-3x" "></span>Aufgabe 7<span class="brainy hdg-rocket fa-2x" "></span><span class="brainy hdg-star fa-2x" "></span><span class="brainy hdg-star fa-2x" "></span>==== | |||
Einer der wichtigsten Nährstoffe für Pflanzen ist Stickstoff. Er wird den Pflanzen (neben dem schon im Boden vorhandenen Stickstoff) in Form von Dünger zugegeben. Wissenschaftler fanden heraus, dass der zusätzliche Getreideertrag | |||
<math>f(x) </math> in 100 kg/ha aufgrund der Zugabe von Dünger sich näherungsweise wie folgt darstellen lässt: | |||
<math>f(x)=\frac{a\cdot x}{x^2+b} </math> mit <math>x\geq0 </math> | |||
Für <math>f</math> gilt dabei <math>f(100)=25 </math> und <math>f(600)=20 </math>. | |||
Was würdest du einem Ökonom für die Zugabe von Dünger empfehlen? | |||
{{Lösung versteckt|Dein Ziel ist es, dass der zusätzliche Getreideertrag möglichst groß wird. Wie sieht die Entwicklung des zusätzlichen Getreideertrages aus? Bestimme die Parameter a und b und skizziere den Funktionsgraphen.|Tipp 1 anzeigen|Tipp 1 verbergen}} | |||
{{Lösung versteckt|Wie viel Dünger muss hinzugegeben werden, um einen größtmöglichen zusätzlichen Getreideertrag zu erzielen?|Tipp 2a anzeigen|Tipp 2a verbergen}} | |||
{{Lösung versteckt|Bestimme das Maximum der Funktion.|Tipp 2b anzeigen|Tipp 2b verbergen}} | |||
{{Lösung versteckt|[[Datei:Lösung A7.jpg|ohne|mini|624x624px]]|Lösung anzeigen|Lösung verbergen}} | |||
{{Fortsetzung|vorher=zurück|vorherlink=Funktionsuntersuchung}} | {{Fortsetzung|vorher=zurück|vorherlink=Funktionsuntersuchung}} | ||
Aktuelle Version vom 16. Januar 2023, 11:55 Uhr
Aufgabe 1
Untersuche die Funktion auf Symmetrie. Bestimme die Schnittpunkte mit den Achsen, ggf. das Verhalten an den Definitionslücken, das Verhalten im Unendlichen und die Extrema. Skizziere anschließend .
a)
b)
c)
d)
e)
Aufgabe 2
Untersuche die Funktion f soweit, dass du den Graphen skizzieren kannst. Bestimme anschließend graphisch und rechnerisch die Gleichung der Tangente
a) ;
b) ;
Aufgabe 3
Betrachtet werden die Funktionen
a) Stelle den Parameter a jeweils so ein, dass du bzw. erhältst. Vergleiche die Anzahl der Extrema der drei Funktionen.
b) Alle drei Funktionsterme haben die Form . Für welche Parameterwerte besitzen die Funktionen, die diese Form haben, zwei Extrema, einen Terrassenpunkt bzw. kein Extremum? Beweise deine Überlegungen auch rechnerisch.
Falls dir das GeoGebra-Applet nicht richtig angezeigt wird, lade die Seite neu.

Aufgabe 4
Aufgabe 5
Seit Jahrtausenden wird die Mistel in der Heilbehandlung eingesetzt. In neuester Zeit wird der Mistelwirkstoff Lektin bei der Behandlung von Krebspatienten verwendet. Mistellektine steigern die Anzahl und die Aktivität der NK-Zellen (Natürliche Killerzellen, die direkt an der Tumorabwehr beteiligt sind):
Die Erhöhung E der Aktivität der NK-Zellen (in %) durch Lektinpräparate hängt entscheidend von der Dosis x (in pro kg Körpergewicht) ab. Sie kann für näherungsweise durch beschrieben werden.
a) Bestimme die Dosis, bei welcher die Wirkung am größten ist.
b) Bestimme die Dosis, ab welcher das Präparat sogar schädlich ist.
Aufgabe 6
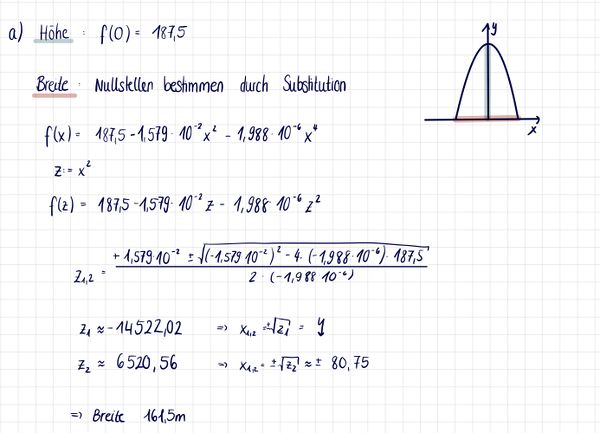
Der Innenbogen des "Gateway-Arch" in St. Louis (USA) lässt sich näherungsweise durch die Funktion (x in m) beschreiben.
a) Berechne die Höhe und die maximale Breite des Innenbogens.
b) Bestimme die Größe des Winkels zwischen dem Innenbogen und der Grundfläche.
c) Bei einer Flugveranstaltung soll ein Flugzeug mit einer Flügelspannweite von 18m unter dem Bogen hindurchfließen. Welche Maximalflughöhe muss der Pilot einhalten, wenn in vertikaler und in horizontaler Richtung ein Sicherheitsabstand zum Bogen von 10m eingehalten werden muss?
Aufgabe 7
Einer der wichtigsten Nährstoffe für Pflanzen ist Stickstoff. Er wird den Pflanzen (neben dem schon im Boden vorhandenen Stickstoff) in Form von Dünger zugegeben. Wissenschaftler fanden heraus, dass der zusätzliche Getreideertrag
in 100 kg/ha aufgrund der Zugabe von Dünger sich näherungsweise wie folgt darstellen lässt:
mit
Für gilt dabei und .
Was würdest du einem Ökonom für die Zugabe von Dünger empfehlen?