Benutzer:HWollny/Expertengruppe1: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
(Die Seite wurde neu angelegt: „<br /> == Expertengruppe 1 == {{Box-spezial|Titel=<div align="center"> '''<math>f(x)=-2x^2</math>''' <span style="color:#C8C8C8"> hallo </span><math>f(x)=-…“) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
== Expertengruppe 1 == | == Expertengruppe 1 == | ||
<gallery widths="200" heights="200" style="text-align:center"> | |||
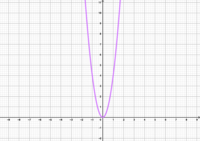
Datei:4 1.png|</span><math>f(x)=4x^2</math> | |||
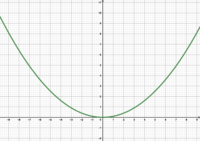
Datei:0.1 1.png|<math>f(x)=0,1x^2</math> | |||
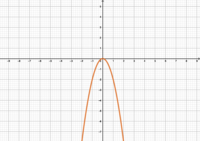
Datei:-2 1.png|<math>f(x)=-2x^2</math> | |||
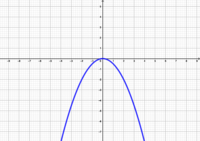
Datei:-0.5 1.png|<math>f(x)=-0,5x^2</math> | |||
</gallery> | |||
<span class="brainy hdg-skill-share fa-5x">'''<u> Austausch </u>''' | {{Box-spezial|Titel= |Inhalt=Für jede der obenstehenden Funktionen ist eine/r von euch Expertin bzw. Experte.|Farbe=Üben|Rahmen=1|Rahmenfarbe=#a0a0a0|Hintergrund=#C8C8C8}} | ||
# Stellt euch gegenseitig vor, welche Informationen ihr über die | |||
<span class="brainy hdg-skill-share fa-5x"></span>'''<u> Austausch </u>''' | |||
# Stellt euch gegenseitig vor, welche Informationen ihr über die Form einer Parabel anhand der Funktionsgleichung ablesen könnt. <small>''Nutzt dazu euer Vorbereitungsblatt und das Bild, mit eurem Funktionsgraphen''</small> | |||
# Beschreibt anschließend in den Sprechblasen auf dem Arbeitsblatt, wie die Funktion <math> f(x)=-3x^2</math> im Vergleich zur Normalparabel verläuft. | # Beschreibt anschließend in den Sprechblasen auf dem Arbeitsblatt, wie die Funktion <math> f(x)=-3x^2</math> im Vergleich zur Normalparabel verläuft. | ||
# Überprüft eure Beschreibung mithilfe von GeoGebra. | # Überprüft eure Beschreibung mithilfe von GeoGebra. | ||
<ggb_applet id=" | <ggb_applet id="zsmzyhc8" width="700" height="550" /> | ||
<span class="brainy hdg-file02 fa-5x"></span>'''<u> Verallgemeinerung </u>''' | <span class="brainy hdg-file02 fa-5x"></span>'''<u> Verallgemeinerung </u>''' | ||
Vervollständigt den Merksatz für den Parameter a auf dem Arbeitsblatt "Merksatz" (zunächst mit Bleistift) | |||
<span class="brainy hdg-space-shuttle fa-5x"></span>'''<u>Schon fertig?!</u>''' | <span class="brainy hdg-space-shuttle fa-5x"></span>'''<u>Schon fertig?!</u>''' | ||
'''gestaucht - gestreckt - nach unten geöffnet - nach oben geöffnet - gespiegelt ''' | |||
Ordnet den Graphen im Koordinatensystem die passende Beschreibung zu. | |||
Wenn ihr auf die Markierung klickt, erscheinen die Antwortmöglichkeiten. | |||
{{LearningApp|app=p892ntm0522|width:100%|height:500px}} | |||
Aktuelle Version vom 16. August 2022, 07:35 Uhr
Expertengruppe 1
Austausch
- Stellt euch gegenseitig vor, welche Informationen ihr über die Form einer Parabel anhand der Funktionsgleichung ablesen könnt. Nutzt dazu euer Vorbereitungsblatt und das Bild, mit eurem Funktionsgraphen
- Beschreibt anschließend in den Sprechblasen auf dem Arbeitsblatt, wie die Funktion im Vergleich zur Normalparabel verläuft.
- Überprüft eure Beschreibung mithilfe von GeoGebra.

Verallgemeinerung
Vervollständigt den Merksatz für den Parameter a auf dem Arbeitsblatt "Merksatz" (zunächst mit Bleistift)
Schon fertig?!
gestaucht - gestreckt - nach unten geöffnet - nach oben geöffnet - gespiegelt
Ordnet den Graphen im Koordinatensystem die passende Beschreibung zu. Wenn ihr auf die Markierung klickt, erscheinen die Antwortmöglichkeiten.