Lernpfad 8a - Volumina und Flächen/Kreisumfang: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Box|Info|Auf dieser Seite erkundest du den Umfang eines Kreises, erfährst was der Kreis mit der Zahl π zu tun hat und lernst, wie man diesen berechnet.|Kurzinfo
{{Box|Info|Auf dieser Seite erkundest du den Umfang eines Kreises, erfährst was der Kreis mit der Zahl π zu tun hat und lernst, wie man den Umfang berechnet.|Kurzinfo
}}
}}


==<span class="brainy hdg-magnifying-glass fa-1,5x"></span> Erste Erkundungen==
<span style="color: #6A93B0"> Jannis </span> und <span style="color: orange"> Paula </span> überlegen, wie sie den Umfang eines Kreises berechnen können.
[[Datei:Kreisumfang_Annaeherung.png|500x500px]]{{Box|Aufgabe 1|Beschreibe Jannis und Paulas Ideen in eigenen Worten. Zeichne einen Kreis mit einem Radius von 5cm in dein Heft unter der Überschrift <i>"1 Umfang und Flächeninhalt eines Kreises - 1.1 Umfang eines Kreises"</i>. Berechne den Kreisumfang näherungsweise mit <u>beiden</u> Vorgehensweisen. Benenne Vor- und Nachteile von Jannis' und Paulas Methode.|Übung
}}Welche erste Abschätzung für den Kreisumfang lässt sich aus den beiden Vorgehensweisen erkennen? Kreuze alle richtigen Antwortmöglichkeiten an.<div class="multiplechoice-quiz">
Der Umfang ist größer als (1x Durchmesser) (2x der Durchmesser) (3x der Durchmesser) (!4x der Durchmesser)
Der Umfang ist kleiner als (!1x der Durchmesser) (!2x der Durchmesser)  (!3x der Durchmesser) (4x der Durchmesser)
</div>


==<span class="brainy hdg-lab-flask03 fa-2x"></span> Forscherauftrag==
==<span class="brainy hdg-lab-flask03 fa-2x"></span> Forscherauftrag==
[[Datei:Kreise_Gegenstand.jpg|250x250px|Kreisförmige Gegenstände im Alltag]]
[[Datei:Kreise_Gegenstand.jpg|250x250px|Kreisförmige Gegenstände im Alltag]]


Kreise begegnen uns vielfach im Alltag. Suche dir <u>mindestens fünf</u> kreisrunde Gegenstände. Bestimme den Durchmesser und den Umfang dieser Gegenstände, indem du geeignete Messinstrumente verwendest (z.B. Lineal, Faden, Maßband).
Kreise begegnen uns vielfach im Alltag. Suche dir <u>mindestens fünf</u> kreisrunde Gegenstände im Klassenzimmer. Bestimme den Durchmesser und den Umfang dieser Gegenstände, indem du geeignete Messinstrumente verwendest (z.B. Lineal, Faden, Maßband).


Halte deine Ergebnisse in einer Tabelle in deinem Heft unter der Überschrift fest.
Halte deine Ergebnisse in einer Tabelle in deinem Heft unter der Überschrift fest.
Zeile 31: Zeile 22:
}}{{Lösung versteckt|Pia hat folgende Messergebnisse. Sie schaut sich das Verhältnis von Umfang und Durchmesser <math>\frac{U}{d}</math> an und ergänzt ihre Tabelle.
}}{{Lösung versteckt|Pia hat folgende Messergebnisse. Sie schaut sich das Verhältnis von Umfang und Durchmesser <math>\frac{U}{d}</math> an und ergänzt ihre Tabelle.
[[Datei:Beispiellösung Erkundung1.png|300px]]
[[Datei:Beispiellösung Erkundung1.png|300px]]
Welches Muster lässt sich hier erkennen? Überprüfe deine Vermutung an deinen eigenen Messwerten.|Tipps anzeigen|Tipps verbergen}}Überprüfe deine Vermutung mithilfe des Applets. Du kannst die Genauigkeit deiner Messungen kontrollieren und weitere Daten sammeln. Sollte das Applet nicht richtig laden, klicke [https://www.geogebra.org/m/vy4TJ2rU].<ggb_applet id="vy4TJ2rU" width="750" height="500" />
Welches Muster lässt sich hier erkennen? Überprüfe deine Vermutung an deinen eigenen Messwerten.|Tipps anzeigen|Tipps verbergen}}
 
==Der Kreisumfang==
{{Box|Merke|Der Umfang U eines Kreises ist ungefähr dreimal so groß wie sein Durchmesser d. Genauer beschreibt die Kreiszahl <math>\pi\approx 3,14</math> das Verhältnis zwischen dem Umfang und dem Durchmesser: Für einen Kreis mit dem Radius <math>r</math> und dem Durchmesser <math>d=2r </math> gilt
<blockquote><math>U= d \cdot \pi = 2 \cdot r \cdot \pi  </math>.</blockquote>
Ergänze deinen Hefteintrag um eine Skizze und ein Beispiel.|Merksatz
}}
 
==<span class="brainy hdg-star fa-1x"></span> Die Kreiszahl π== 
Beim Kreis ist das Verhältnis von Umfang U und Durchmesser d ist immer gleich.
 
Dieses Verhältnis wird '''Kreiszahl π''' genannt.  = π = 3,141... Dieser Dezimalbruch endet nie. π ist also kein Element der rationalen Zahlen.
 
Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden, schaus' dir an:
{{#ev:youtube|KIZOpIcBEnI|800|center}}
 
 
Und nun noch einige kurze Infos zur Kreiszahl π:
 
*eine der bekanntesten und sagenumwobensten Zahlen der Mathematik
*Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet
*mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14)
*Mittlerweile (2021) von Schweizer Forschern auf ca. 62,8 Billionen Dezimalstellen berechnet
*beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist:
 
π =  = 3,14159...
 
*Ein Kreis mit dem Durchmesser 1 hat somit einen Umfang von π.


Tastenkombination für die Kreiszahl π für Berechnungen mit dem Taschenrechner:
Vergleicht eure Ergebnisse mit anderen Zweierteams und besprecht sie anschließend mit Frau Krause.  
[[Datei:Taschenrechner pi.png|mini|alternativtext=|ohne|281x281px]]


==<span class="brainy hdg-ruler-compasses fa-2x"></span> Übungen== 
{{Fortsetzung|vorher=zurück|vorherlink=../Kreise|weiter=Merksatz|weiterlink=../Hefteintrag Umfang Kreis}}
{{Box|Aufgabe 2|Berechne den Kreisumfang. Runde auf zwei Nachkommastellen.
# Der Radius des Kreises beträgt <math>r=3</math>cm.
# Der Radius des Kreises beträgt <math>r=5</math>mm.
# Der Radius des Kreises beträgt <math>d=12</math>cm.
# Der Radius des Kreises beträgt <math>d=8</math>m.|Übung
}}{{Lösung versteckt|Lösungen:
# <math>U=2\cdot 3cm \cdot \pi \approx 18,85cm</math>
# <math>U=2\cdot 5mm \cdot \pi \approx 31,42mm</math>
# <math>U=12cm \cdot \pi \approx 37,7cm</math>
# <math>U=8m \cdot \pi \approx 25,13cm</math>|Lösung anzeigen|Lösung verbergen}}{{Box|Aufgabe 3|Bestimme die Länge der Strecke, die ein Fahrrad mit einem 26-Zoll-Reifen bei einer Radumdrehung zurück legt.  
''Hinweis'': 1 Zoll entspricht 2,54cm|Übung
}}{{Lösung versteckt|Der Raddurchmesser beträgt 26 Zoll und damit 66,04 cm. Es gilt
<math> U= 66,04 cm \cdot \pi \approx 207,47 cm </math>.
Mit einer Umdrehung legt das Fahrrad 207,47 cm zurück.|Lösung anzeigen|Lösung verbergen}}{{Fortsetzung|weiter=Die Kreisfläche erkunden|weiterlink=Lernpfad 8a - Volumina und Flächen/Kreisfläche}}

Aktuelle Version vom 23. Juni 2023, 09:14 Uhr

Info
Auf dieser Seite erkundest du den Umfang eines Kreises, erfährst was der Kreis mit der Zahl π zu tun hat und lernst, wie man den Umfang berechnet.


Forscherauftrag

Kreisförmige Gegenstände im Alltag

Kreise begegnen uns vielfach im Alltag. Suche dir mindestens fünf kreisrunde Gegenstände im Klassenzimmer. Bestimme den Durchmesser und den Umfang dieser Gegenstände, indem du geeignete Messinstrumente verwendest (z.B. Lineal, Faden, Maßband).

Halte deine Ergebnisse in einer Tabelle in deinem Heft unter der Überschrift fest.

Gegenstand Durchmesser d (in cm) Umfang U (in cm)
... ... ...

Erkundung

Betrachte die Messergebnisse in der Tabelle. Kannst du eine Regelmäßigkeit erkennen?

Untersuche, welcher Zusammenhang zwischen dem Durchmesser d und dem Umfang U des Kreises besteht. Notiere deine Vermutungen.

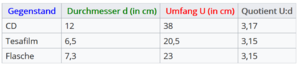
Pia hat folgende Messergebnisse. Sie schaut sich das Verhältnis von Umfang und Durchmesser an und ergänzt ihre Tabelle. Beispiellösung Erkundung1.png

Welches Muster lässt sich hier erkennen? Überprüfe deine Vermutung an deinen eigenen Messwerten.

Vergleicht eure Ergebnisse mit anderen Zweierteams und besprecht sie anschließend mit Frau Krause.

zurück
Merksatz
Abgerufen von „https://unterrichten.zum.de/index.php?title=Lernpfad_8a_-_Volumina_und_Flächen/Kreisumfang&oldid=135138“