|
|
| (158 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | [[Kategorie:Mathematik]] |
| | [[Kategorie:Lernpfad]] |
| | [[Kategorie:Sekundarstufe 1]] |
| | {{Box|Lernpfad|Herzlich willkommen im Lernpfad <b>Prozente und Prozentrechnung</b>! |
|
| |
|
| {{Box|1=Lernpfad|2=
| | <br>Dieser Lernpfad soll dir dabei helfen, dein Wissen aus der Bruchrechnung auf die Prozentrechnung zu übertragen und deine Vorstellung von Prozenten auf- bzw. auszubauen. |
| Herzlich Willkommen in dem Lernpfad "Bruchteil, Anteil und Ganzes bei der Bruchrechnung"!<br><br>
| |
|
| |
|
| Dieser Lernpfad wurde erstellt, um dein Wissen und deine Fähigkeiten im Umgang mit dem Bruchteil, Anteil und Ganzem innerhalb der Bruchrechnung zu verbessern.<br><br>
| | <br><br>Das Schöne daran ist, dass du vieles von dem, was du bereits aus der Bruchrechnung kennst, hier direkt anwenden kannst. |
|
| |
|
| Dafür erhältst du zuerst eine kurze '''Übersicht über Bruchteil, Anteil und Ganzes''', bevor es darum geht, dass du Bruchteil, Anteil und Ganzes in gegebenen Situationen '''erkennen''' kannst. Der dritte Abschnitt ist dazu da, dass du '''Zusammenhänge''' zwischen Bruchteil, Anteil und Ganzes '''erkunden''' kannst. Im vierten Abschnitt wird dir die Möglichkeit geboten, Bruchteil, Anteil oder Ganzes zu '''berechnen''', wenn jeweils die anderen Beiden gegeben sind. Du findest dabei immer zuerst eine Förderaufgabe zur jeweiligen Berechnungsweise, bevor du diese dann in einer weiteren Aufgabe jeweils üben kannst. Im fünften Abschnitt geht es darum, dass du erkennen kannst, ob Bruchteil, Anteil oder Ganzes berechnet werden soll. Zum Schluss kannst du das gelernte Wissen in einem '''Quiz '''überprüfen.<br><br>
| | <br><br>Am Ende dieses Lernpfades sollst du |
| | * den Zusammenhang zwischen Brüchen und Prozenten kennen |
| | * einfache Prozentaufgaben lösen können |
| | * mit dem Prozentstreifen umgehen können |
| | * die Fachbegriffe zur Prozentrechnung kennengelernt haben |
| | |Lernpfad}} |
| | {{Box|Merke| |
| | Der Begriff <b>"Prozent"</b> heißt dabei nichts anderes als <b>"von Hundert"</b>. Du hast es also im Prinzip mit nichts anderem zu tun, als <b>einem Bruch, dessen Nenner immer 100 ist</b>. Hier lernst du, wie du dein Wissen aus der Bruchrechnung in die Prozentrechnung übertragen kannst! |
| | |Merksatz}} |
|
| |
|
| [[Datei:Förderaufgabe.png|100px]] In diesem Lernpfad findest du Aufgaben mit diesem Bild. Diese Aufgaben sind Förderaufgaben und unterstützen dich besonders stark beim Umgang mit den neuen Inhalten. <br><br>
| | <b>Also: Leg los!</b> |
|
| |
|
| Einige Aufgaben sind interaktiv gestaltet. Wenn du alle nötigen Angaben in die dafür vorgesehenen Felder geschrieben hast, oder alle Dinge passend einander zugeordnet hast, dann kannst du deine Lösung überprüfen, indem du auf diesen Button drückst: [[Datei:Eingabebutton.png|40px]]. Dieser befindet sich in der rechten unteren Ecke.<br><br>
| | ==Wiederholung: Bruchteil, Anteil und Ganzes== |
|
| |
|
| In manchen Aufgaben musst du Brüche hinschreiben. Dies gelingt dir, indem du folgende Schreibweise verwendest: Schreibe 1/2 um den Bruch <math> \frac{1}{2} </math> einzutragen.
| | {{Box|Info| |
| |3=Lernpfad}}
| | Zunächst rufen wir uns in Erinnerung, was der Bruchteil, der Anteil und das Ganze in der Bruchrechnung war. Im Rahmen der Bruchrechnung hast du schon einige Beispiele von Prozentsätzen kennengelernt. Wir schauen uns zunächst noch einmal die Begriffe aus der Bruchrechnung an! |
| | | |Kurzinfo}} |
| | |
| ==Was sind nochmal Bruchteil, Anteil und das Ganze?==
| |
| | |
| {{Box|1=Info|2= | |
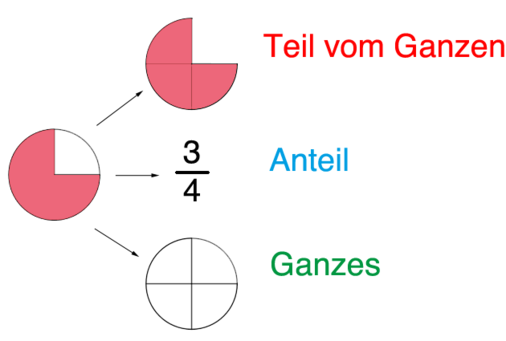
| In diesem Abschnitt kannst du dir nochmal an zwei konkreten Beispielen anschauen, was <span style="color: red">Bruchteil </span>, <span style="color: green">Anteil </span> und <span style="color: blue">Ganzes </span> sind.
| |
| |3=Kurzinfo}}
| |
| | |
| Immer wenn wir einen Bruch gegeben haben, dann können wir den <span style="color: red">Bruchteil </span>, den <span style="color: green">Anteil </span> und das <span style="color: blue">Ganze </span> bestimmen. Als Ausgangspunkt dient das <span style="color: blue">Ganze </span>, von dem nur ein bestimmter Teil betrachtet werden soll (der <span style="color: red">Bruchteil </span>). Der <span style="color: green">Anteil </span> stellt immer das Verhältnis zwischen dem <span style="color: red">Bruchteil </span> und dem <span style="color: blue">Ganzen </span> dar. Der <span style="color: green">Anteil </span> ergibt sich, indem der <span style="color: red">Bruchteil </span> durch das <span style="color: blue">Ganze </span> dividiert wird.
| |
| | |
| In den folgenden zwei Beispielen, kannst du dir diese drei Teile eines Bruches (<span style="color: red">Bruchteil </span>, <span style="color: green">Anteil </span>, <span style="color: blue">Ganzes </span>) mithilfe von zwei Abbildungen anschauen.
| |
|
| |
|
| {{Box|1=Beispiel|2= | | {{Box|1=Beispiel|2= |
| '''Betrachte <math>\frac{3}{4}</math> eines Kreises.'''
| | In diesem Beispiel schauen wir uns noch einmal drei Viertel eines Kreises an. |
| | |
| {{(!}} class=wikitable
| |
| {{!-}}
| |
| {{!}} [[Datei:Darstellung kontinuierliches Ganzes.png|900px]]
| |
| {{!-}}
| |
| {{!}}
| |
| Der gesamte Kreis stellt bei diesem Beispiel das <span style="color: blue">Ganze </span> dar, auf das sich der <span style="color: red">Bruchteil </span> und der <span style="color: green">Anteil </span> beziehen.
| |
| | |
| Das <span style="color: blue">Ganze </span> kann nun in 4 gleich große Teile (4 Viertelkreise) unterteilt werden. Dabei ergeben die 3 farbig markierten Teile zusammen den <span style="color: red">Bruchteil </span>.
| |
| | |
| Der <span style="color: green">Anteil </span> gibt das Verhältnis zwischen dem <span style="color: red">Bruchteil </span> und dem <span style="color: blue">Ganzen </span> wieder. Es sind 3 von 4 Viertelkreisen farbig markiert (→ <math>\frac{3}{4}</math>)
| |
| {{!-}}
| |
| {{!)}}
| |
|
| |
|
| | [[Datei:Darstellung BAG Kreis.png|506px]] |
| |3=Beispiel}} | | |3=Beispiel}} |
| | <br><br> |
| | ==Brüche und Prozentsätze zuordnen== |
|
| |
|
| Im ersten Beispiel wird das <span style="color: blue">Ganze </span> durch eine geometrische Form (Kreis) dargestellt. Du wirst aber auch mit <span style="color: blue">Ganzen </span> arbeiten müssen, welche nur aus einer Menge (Zahl) bestehen. In einem zweiten Beispiel kannst du dir anschauen, was in so einem Fall der <span style="color: red">Bruchteil </span>, <span style="color: green">Anteil </span> und das <span style="color: blue">Ganze </span> sind.
| | {{Box|Üben| |
| | | Zunächst siehst du in der folgenden Aufgabe einige Formen, von denen bestimmte Anteile farbig markiert sind. <b>Gib die farbigen Anteile sowohl in der Bruch- als auch in der Prozentschreibweise an!</b> |
| {{Box|1=Beispiel|2= | | <br>Wenn du mit einer Teilaufgabe fertig bist, kannst du mit dem Pfeil oben links zurück in das Menü gelangen.<br> |
| '''Betrachte nun <math>\frac{3}{4}</math> von 8.'''
| | Um einen Anteil in der Prozentschreibweise schreiben zu können, musst du den Bruch zunächst in einen Bruch mit dem Nenner <u>100</u> umwandeln, indem du ihn entsprechend erweiterst oder kürzt.<br> |
| | | <br><b>Tipp: Bei einigen Aufgaben findest du oben links ein kleines Glühbirnensymbol. Solltest du beim Lösen der Aufgaben Hilfe benötigen, so erhältst du durch einen Klick darauf einen Hinweis!</b><br> |
| {{(!}} class=wikitable | | |Üben}} |
| {{!-}}
| | <iframe src="https://learningapps.org/watch?v=prqmizyq321" style="border:0px;width:800px;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| {{!}} [[Datei:Trias Darstellung diskretes Ganzes 8 Sterne.png|900px]]
| | <br><br> |
| {{!-}}
| | {{Box|Üben| |
| {{!}} Die 8 Sterne stellen in diesem Beispiel das <span style="color: blue">Ganze </span> dar, auf das sich der <span style="color: red">Bruchteil </span> und der <span style="color: green">Anteil </span> beziehen.
| | In der folgenden Aufgabe siehst du einige Brüche und Prozentsätze, die du bestimmt schon kennst. Ordne den Brüche die entsprechenden Prozentsätze zu und überprüfe deine Ergebnisse am Ende mit einem Klick auf den blauen Haken unten rechts!<br> |
| | |Üben}} |
| | <iframe src="https://learningapps.org/watch?v=pn2rsf4a521" style="border:0px;width:800px;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe><br><br> |
| | {{Box|Üben| |
| | Ein wenig schwieriger wird es in der nächsten Aufgabe. Hier sollst du nun ohne Vorgabe von Werten die richtigen Prozentsätze in die Felder eintragen. Viel Erfolg! |
| | |Üben}} |
| | <iframe src="https://learningapps.org/watch?v=pvpwgze6n21" style="border:0px;width:800px;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| | <br><br> |
|
| |
|
| Das <span style="color: blue">Ganze </span> kann nun in 4 gleich große Teile (4 Gruppen mit jeweils 2 Sternen) unterteilt werden. Dabei ergeben die 3 farbig markierten Gruppen (die 6 farbig markierten Sterne) zusammen den <span style="color: red">Bruchteil </span>.
| |
|
| |
|
| Der <span style="color: green">Anteil </span> gibt das Verhältnis zwischen dem <span style="color: red">Bruchteil </span> und dem <span style="color: blue">Ganzen </span> wieder. Es sind 3 von 4 Teilgruppen, die jeweils aus 2 Sternen bestehen, farbig markiert (→ <math>\frac{3}{4}</math>)
| |
| {{!-}}
| |
| {{!)}}
| |
|
| |
|
|
| |
|
| |3=Beispiel}}
| |
|
| |
|
|
| |
|
| Du kannst im nachfolgenden Lückentext überprüfen, ob du nun weißt, was <span style="color: red">Bruchteil </span>, <span style="color: green">Anteil </span> und <span style="color: blue">Ganzes </span> sind.
| | ==Arbeiten mit dem Bruch- und Prozentstreifen== |
| <div class="lueckentext-quiz">
| |
| Wenn du einen Bruch in einer Sachsituation gegeben hast, dann kannst du bei dem Bruch immer Bruchteil, Anteil und '''Ganzes''' betrachten. Das Ganze stellt den '''Ausgangspunkt''' dar, auf welchen sich der '''Bruchteil''' und der Anteil beziehen. Bei Brüchen wird meist nur ein gewisser '''Teil''' des Ganzen betrachtet. Dabei handelt es sich um den Bruchteil. Das Verhältnis zwischen Bruchteil und Ganzem spiegelt sich im '''Anteil''' wieder.
| |
| </div>
| |
|
| |
|
| ==Bruchteil, Anteil und Ganzes erkennen==
| |
|
| |
|
| {{Box|1=Info|2= | | {{Box|Info| |
| In diesem Abschnitt geht es darum, dass du aus beschriebenen Kontexten den Bruchteil, Anteil und das Ganze erkennen kannst. Nur wenn dir das gelingt, kannst du im weiteren Verlauf mit Bruchteil, Anteil und Ganzem rechnen. | | Bestimmt kennst du aus der Bruchrechnung noch Übungsmaterial Material wie z.B. den Bruchstreifen. |
| |3=Kurzinfo}} | | <br>In der Prozentrechnung arbeitet man am besten mit dem <b>Prozentstreifen</b>. |
| | <br>Direkt unter diesem Text findest du einen interaktive Bruch- und Prozentstreifen, an denen du zunächst frei experimentieren kannst. |
| | <br>Wenn du den Mauszeiger auf das Fenster mit den Streifen führst, kannst du mit dem Mausrad auch weiter hinauszoomen, falls das Fenster für einen länger eingestellten Streifen zu klein sein sollte. |
| | |Kurzinfo}} |
|
| |
|
| | <iframe src="https://www.geogebra.org/classic/fcy4cfxr?embed" width="800" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe> |
|
| |
|
| {{Box|1=1. Was ist mein Bruchteil, mein Anteil und mein Ganzes?|2=
| | <br> |
| | <br><iframe src="https://learningapps.org/watch?v=pxfj04pt321" style="border:0px;width:800px;height:800px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| | <br><br> |
|
| |
|
| {{LearningApp|app=p827e0nwt19|width=100%|height=450px}} | | {{Box|Üben| |
| | | <b>Bestimme nun mit dem interaktiven Bruch- und Prozentstreifen 2/5 von 120 kg!</b> |
| {{Lösung versteckt| 1=
| | |Üben}} |
| | | <iframe src="https://www.geogebra.org/classic/kthcevrh?embed" width="800px" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe> |
| {{Lösung versteckt|1=
| |
| Ganze:[[Datei:Kreis Ganze 8.png|250px]] <math> \qquad \qquad </math> Bruchteil: [[Datei:Kreis Bruchteil drei.png|200px]] <math> \qquad \qquad </math> Anteil: <math>\quad</math> <math> \frac{3}{8} </math>
| |
| |2=Lösung: Aufgabe 1|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: [[Datei:Rechteck Ganze 6 neu.png|275px]] <math> \qquad \qquad </math> Bruchteil: [[Datei:Rechteck Bruchteil 5 neu.png|250px]] <math> \qquad \qquad </math> Anteil: <math>\quad</math><math> \frac{5}{6} </math>
| |
| |2=Lösung: Aufgabe 2|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: [[Datei:Dreieck Ganze 6.png|250px]] <math>\qquad \qquad </math> Bruchteil: [[Datei:Dreieck Bruchteil 2.png|250px]] <math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{2}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{1}{3} </math>
| |
| |2=Lösung: Aufgabe 3|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: [[Datei:Kuriose Form Ganze 16.png|250px]] <math>\qquad \qquad </math> Bruchteil: [[Datei:Kuriose Form Bruchteil 6.png|250px]]<math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{2}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{1}{3} </math>
| |
| |2=Lösung: Aufgabe 4|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 20 <math>\qquad \qquad </math> Bruchteil: 6 <math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{3}{10} </math>
| |
| |2=Lösung: Aufgabe 5|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 7 <math>\qquad \qquad </math> Bruchteil: 2 <math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{2}{7} </math>
| |
| |2=Lösung: Aufgabe 6|3=Verstecken}} | |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 28 <math>\qquad \qquad </math> Bruchteil: 18 <math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{18}{28} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{9}{14} </math>
| |
| |2=Lösung: Aufgabe 7|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 120 <math>\qquad \qquad </math> Bruchteil: 20 <math>\qquad \qquad </math> Anteil:<math>\quad</math> <math> \frac{20}{120} \quad \overset{\text{kürzen}}{\underset{\text{mit 20}}{=}} \quad \frac{1}{6} </math>
| |
| |2=Lösung: Aufgabe 8|3=Verstecken}}
| |
| | |
| |2=Lösungen|3=Verstecken}}
| |
| |3=Arbeitsmethode}}
| |
| | |
| | |
| ==Zusammenhänge erkunden==
| |
| | |
| {{Box|1=Info|2=
| |
| In diesem Abschnitt kannst du Zusammenhänge zwischen Bruchteil, Anteil und Ganzem erkunden. Du kannst zum Beispiel herausfinden, auf welche Art und Weise sich der Bruchteil verändert, wenn der Anteil gleich bleibt, aber das Ganze größer oder kleiner wird.
| |
| |3=Kurzinfo}}
| |
| | |
| {{Box|1=2. Erkunde einige Zusammenhänge selbstständig|2=
| |
| | |
| Ziel dieser Aufgabe ist es, deine Entdeckungen in Geogebra in Merksätze zu formulieren.
| |
| | |
| Gehe bei der nun folgenden Übung wie folgt vor:
| |
| | |
| 1. Schaue dir die angefangenen Sätze unter den Aufgabenstellungen an.<br>
| |
| 2. Stelle Vermutungen auf, wie sich Bruchteil (blau gefärbtes Rechteck), Anteil oder Ganzes (schwarz umrandetes Rechteck) in den jeweiligen Situationen verändern und schreibe deine Vermutungen auf einem Blatt Papier auf.<br>
| |
| 3. Scrolle nun weiter nach unten. Dort findest du vier Geogebra Applets. Untersuche nun die Veränderungen in den Geogebra Applets. Klicke dafür einfach auf diese und verändere mithilfe der Schieberegler die jeweils zugehörige Größe. In den Geogebra Applets ist das Ganze ist immer das schwarz umrandete Rechteck und der Bruchteil immer der blau gefärbte Teil des Rechtecks.<br>
| |
| 4. Vervollständige nun die angefangenen Sätze unter den Aufgabenstellungen und vergleiche sie mit deinen vorher aufgeschriebenen Vermutungen.<br>
| |
| 5. Überprüfe nun die vervollständigten Sätze. Schaue dir noch einmal die Geogebra Applets genau an, falls die Sätze nicht richtig sind.<br>
| |
| | |
| {{LearningApp|app=pdd77dvsk19|width=100%|height=400px}}
| |
| | |
| <ggb_applet id="twujyngd" width="100%" height="200" />
| |
| <ggb_applet id="tjxa23bx" width="100%" height="200" />
| |
| <ggb_applet id="xtggrgq8" width="100%" height="200" />
| |
| <ggb_applet id="u8dhqzg7" width="100%" height="200" />
| |
| | |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| | |
| ==Mit Bruchteil, Anteil und Ganzem rechnen==
| |
| | |
| {{Box|1=Info|2=
| |
| Für diesen Abschnitt ist es wichtig, dass du erkennen kannst, was der Bruchteil, Anteil und das Ganze in einer bestimmten Situation ist. Falls du noch etwas unsicher beim Erkennen von Bruchteil, Anteil und Ganzem bist, dann schau nochmal in dem entsprechenden Abschnitt weiter oben nach.
| |
| |3=Kurzinfo}}
| |
| | |
| ===Der Bruchteil ist gesucht===
| |
| | |
| In diesem Abschnitt ist immer der Anteil und das Ganze gegeben und es wird der Bruchteil gesucht. Wenn du nicht mehr weißt, wie du aus dem Anteil und dem Ganzen den Bruchteil berechnen kannst, dann schaue in die nachfolgende Erklärung.
| |
| | |
| <div style="margin-left:2em">
| |
| <!--{{Lösung versteckt|1=Text zum Verstecken|2=Label fürs Anzeigen|3=Label fürs Verbergen}}-->
| |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Der Bruchteil gibt die Anzahl an Teilen wieder, die vom Ganzen ausgewählt werden.<br>
| |
| Er lässt sich berechnen, indem du den Anteil mit dem Ganzen multiplizierst.</big><br>
| |
| <br><br> | | <br><br> |
| '''Beispiel:'''
| |
|
| |
| Julia und Marvin besitzen zusammen 6 Mützen. <math>\frac{2}{3}</math> davon gehören Marvin und <math> \frac{1}{3} </math> gehören Julia. Wie viele Mützen gehören Marvin?
| |
|
| |
| Rechnung: Wir multiplizieren <math>\frac{2}{3} </math> mit 6 und erhalten <math>\frac{2}{3} \cdot 6 = \frac{12}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} 4 </math> .<br>
| |
| Antwort: Marvin besitzt 4 Mützen.
| |
| |3=Merksatz}}
| |
|
| |
| |2=Erklärung: Bruchteil berechnen|3=Verstecken}}</div>
| |
|
| |
|
| | <iframe src="https://learningapps.org/watch?v=p5sm3iiqt21" style="border:0px;width:800px;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe><br><br> |
|
| |
|
| {{Box|1= 3. Wie berechne ich den Bruchteil? [[Datei:Förderaufgabe.png|100px]] | 2= | | {{Box|Üben| |
| | <b>Bestimme 3/10 von 150 m. <u>Zeichne dir einen entsprechenden Bruchstreifen in dein Heft.</u></b> |
| | |Üben}} |
| | <iframe src="https://www.geogebra.org/classic/b8jgrejv?embed" width="800" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe><br><br> |
|
| |
|
| <div class="lueckentext-quiz" width="200" height="160">
| |
| Der Bruchteil lässt sich mithilfe der allgemeinen Berechnungsweise '''Bruchteil''' = Anteil <math> \cdot </math>'''Ganze''' berechnen.
| |
| Wir üben nun gemeinsam die Berechnung des Bruchteils in einem gegebenen Sachzusammenhang:
| |
|
| |
|
| Kim kauft für ihre Geburtstagsfeier Schokoladenriegel. Von den 24 Riegeln sind <math>\frac{2}{3}</math> mit Nüssen, <math> \frac{1}{4}</math> mit Kokos und <math>\frac{1}{12} </math> mit Karamell. Berechne die Anzahl an gekauften Schokoladenriegeln mit Nüssen.
| | {{Lösung versteckt|3/10 von 150 m entsprechen <b>45 m</b>.|Überprüfe hier deine Lösung!|Lösung verbergen}} |
| | |
| Rechnung:
| |
| Anteil= '''<math>\frac{2}{3}</math>''' Ganze = '''24''' <math> \qquad </math>
| |
| | |
| Bruchteil = '''<math>\frac{2}{3} </math>''' <math>\cdot </math>'''24''' <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} </math> '''<math> \frac{2}{1} </math>''' <math> \cdot </math> '''8''' = '''16'''.
| |
| | |
| Antwort: Kim hat für ihre Geburtstagsfeier 16 Schokoladenriegel mit Nüssen gekauft.
| |
| </div>
| |
| | |
| {{Lösung versteckt|1= | |
| Der Bruchteil lässt sich mithilfe der allgemeinen Berechnungsweise Bruchteil = Anteil <math> \cdot </math>Ganze berechnen.
| |
| Wir üben nun gemeinsam die Berechnung des Bruchteils in einem gegebenen Sachzusammenhang:
| |
| | |
| Kim kauft für ihre Geburtstagsfeier Schokoladenriegel. Von den 24 Riegeln sind <math>\frac{2}{3}</math> mit Nüssen, <math> \frac{1}{4}</math> mit Kokos und <math>\frac{1}{12} </math> mit Karamell. Berechne die Anzahl an gekauften Schokoladenriegeln mit Nüssen.
| |
| | |
| Rechnung:
| |
| Anteil= <math>\frac{2}{3}</math> Ganze = 24 <math> \qquad </math>
| |
| | |
| Bruchteil = <math>\frac{2}{3} </math> <math>\cdot </math>24 <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} </math> <math> \frac{2}{1} </math> <math> \cdot </math> 8 = 16.
| |
| | |
| Antwort: Kim hat für ihre Geburtstagsfeier 16 Schokoladenriegel mit Nüssen gekauft.
| |
| |2=Lösung|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| {{Box|1=4. Den Bruchteil berechnen|2=
| |
| | |
| Berechne nun eigenständig den Bruchteil in den dargestellten Aufgaben in deinem Heft. Kürze dabei soweit wie möglich. Bei den Antworten musst du keine Einheiten angeben.
| |
| | |
| Wenn du auf diesen Button [[Datei:Vollbildschirmmodus.png|30px]] in der rechten oberen Ecke klickst, dann gelangst du in den Vollbildmodus.
| |
| | |
| Nachdem du alle Bruchteile berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe die Lösung in das freie Feld einträgst und am Ende auf [[Datei:Eingabebutton.png|40px]] drückst.
| |
| | |
| {{LearningApp|app=p22jxrmyc19|width=100%|height=400px}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du nicht weißt, wie du die Aufgaben lösen kannst, dann schaue dir die versteckte Erklärung vor Aufgabe 3 und die Aufgabe 3 noch einmal genau an.
| |
| | |
| |2= Tipp zum Lösen der Aufgaben|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Du multiplizierst einen Bruch mit einer natürlichen Zahl, indem du den Zähler mit der natürlichen Zahl multiplizierst und den Nenner beibehältst.</big><br>
| |
| <br><br> | | <br><br> |
| | | Jetzt arbeiten wir nicht mehr mit Brüchen, sondern mit Prozenten. Dazu können wir auch den bekannten Streifen verwenden. Da Prozente nichts anderes sind als Hunderterbrüche, muss am Streifen immer ein Hunderterbruch eingestellt werden. |
| '''Beispiel:'''
| |
| | |
| Der Bruch <math>\frac{2}{3}</math> soll mit der natürlichen Zahle <math> 6 </math> multipliziert werden. Wir multiplizieren dann den Zähler (<math>2</math>) mit der natürlichen Zahl <math>6</math> und behalten den Nenner (<math>3</math>) bei.
| |
| | |
| → <math> \frac{2}{3} \cdot 6 = \frac{2 \cdot 6}{3} = \frac{12}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} \quad 4 </math><br><br>
| |
| | |
| Alternativ kannst du schon vorher kürzen.<br><br>
| |
| | |
| → <math> \frac{2}{3} \cdot 6 \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} \quad \frac{2}{1} \cdot 2 = \frac{4}{1} = 4 </math>
| |
| | |
| |3=Merksatz}}
| |
| |2=Hilfestellung: Bruch mit natürlicher Zahl multiplizieren|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Du kannst einen Bruch kürzen, indem du den Zähler und den Nenner durch die gleiche Zahl dividierst.</big><br>
| |
| <br><br> | | <br><br> |
|
| |
|
| '''Beispiel:'''
| | {{Box|Üben| |
| | | <b>Bestimme 90 % von 100 kg Mehl.</b> |
| Der Bruch <math>\frac{16}{18}</math> soll gekürzt werden. Sowohl der Zähler (16) als auch der Nenner (18) sind durch 2 teilbar.
| | |Üben}} |
| | <iframe src="https://www.geogebra.org/classic/cwjqbexn?embed" width="800" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe><br><br> |
| | {{Lösung versteckt|90 % von 100 kg Mehl entsprechen <b>90 kg</b> Mehl.|Überprüfe hier deine Lösung!|Lösung verbergen}} |
|
| |
|
| → <math> \frac{16 : 2}{18 : 2} = \frac{8}{9} </math>
| |
|
| |
|
| |3=Merksatz}}
| | {{Box|Üben| |
| |2=Hilfestellung: Kürzen|3=Verstecken}}
| | <b>Bestimme 90 % von 20 kg Mehl. Zeichne dir einen entsprechenden Bruchstreifen in dein Heft.</b> |
| | | |Üben}} |
| {{Lösung versteckt|1= | | <iframe src="https://www.geogebra.org/classic/hgffkggn?embed" width="800" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe><br><br> |
| | | {{Lösung versteckt|90 % von 20 kg Mehl entsprechen <b>18 kg</b> Mehl.|Überprüfe hier deine Lösung!|Lösung verbergen}} |
| {{Lösung versteckt|1=
| |
| Ganze: 32 <math>\qquad</math> Anteil: <math> \frac{3}{8}</math> <br><br>
| |
| <math>\frac{3}{8} \cdot 32 = \frac{96}{8} \quad \overset{\text{kürzen}}{\underset{\text{mit 8}}{=}} \quad 12 </math><br><br>
| |
| oder<br><br>
| |
| <math>\frac{3}{8} \cdot 32 \quad \overset{\text{kürzen}}{\underset{\text{mit 8}}{=}} \quad \frac{3}{1} \cdot 4 = 12 </math>
| |
| |2=Lösung: Aufgabe 1|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 60 <math>\qquad</math> Anteil: <math> \frac{10}{12}</math> <br><br>
| |
| <math>\frac{10}{12} \cdot 60 = \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{5}{6} \cdot 60 = \frac{300}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 6}}{=}} \quad 50 </math><br><br>
| |
| oder<br><br>
| |
| <math>\frac{10}{12} \cdot 60 = \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{5}{6} \cdot 60 \quad \overset{\text{kürzen}}{\underset{\text{mit 6}}{=}} \quad = \frac{5}{1} \cdot 10 = 50 </math>
| |
| |2=Lösung: Aufgabe 2|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 200 <math>\qquad</math> Anteil: <math> \frac{3}{10}</math> <br><br>
| |
| <math>\frac{3}{10} \cdot 200 = \frac{600}{10} \quad \overset{\text{kürzen}}{\underset{\text{mit 10}}{=}} \quad 60 </math><br><br>
| |
| oder<br><br>
| |
| <math>\frac{3}{10} \cdot 200 \quad \overset{\text{kürzen}}{\underset{\text{mit 10}}{=}} \quad \frac{3}{1} \cdot 20 = 60 </math>
| |
| |2=Lösung: Aufgabe 3|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 36 <math>\qquad</math> Anteil: <math> \frac{5}{6}</math> <br><br>
| |
| <math>\frac{5}{6} \cdot 36 = \frac{180}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 6}}{=}} \quad 30 </math><br><br>
| |
| oder<br><br>
| |
| <math>\frac{5}{6} \cdot 36 \quad \overset{\text{kürzen}}{\underset{\text{mit 6}}{=}} \quad \frac{5}{1} \cdot 6 = 30 </math>
| |
| |2=Lösung: Aufgabe 4|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1= | |
| Ganze: 35 <math>\qquad</math> Anteil: <math> \frac{3}{7}</math> <br><br>
| |
| <math>\frac{3}{7} \cdot 35 = \frac{105}{7} \quad \overset{\text{kürzen}}{\underset{\text{mit 7}}{=}} \quad 15 </math><br><br>
| |
| oder<br><br>
| |
| <math>\frac{3}{7} \cdot 35 \quad \overset{\text{kürzen}}{\underset{\text{mit 7}}{=}} \quad \frac{3}{1} \cdot 5 = 15 </math>
| |
| |2=Lösung: Aufgabe 5|3=Verstecken}} | |
| | |
| |2=Lösungen|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| ===Das Ganze ist gesucht===
| |
| | |
| In diesem Abschnitt ist immer der Bruchteil und der Anteil gegeben und es wird das Ganze gesucht.
| |
| | |
| Damit du das Ganze berechnen kannst, musst du wissen, wie du eine natürliche Zahl durch einen Bruch dividieren kannst. Falls du nicht mehr genau weißt, wie das funktioniert, dann schaue in die versteckte Hilfestellung rein.
| |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Du kannst eine natürliche Zahl durch einen Bruch dividieren, indem du die natürliche Zahl mit dem Kehrbruch des gegebenen Bruchs multiplizierst. Der Kehrbruch zu einem gegebenen Bruch erhältst du, indem du Zähler und Nenner des Bruchs vertauschst.</big><br>
| |
| <br><br> | | <br><br> |
|
| |
|
| '''Beispiel:'''
| | {{Box|Üben| |
| | | Versuche diese Aufgaben nun ohne Applet (also ohne den interaktiven Bruch- und Prozentstreifen) zu lösen. Wenn du willst, zeichne dir einen entsprechenden Prozentstreifen in dein Heft. |
| Die natürliche Zahl 2 soll durch <math>\frac{2}{4}</math> dividiert werden. Der Kehrbruch von <math>\frac{2}{4}</math> ist <math>\frac{4}{2}</math>. Wir multiplizieren nun 2 mit dem Kehrbruch (<math>\frac{2}{4}</math>)
| | |Üben}} |
| | | <iframe src="https://learningapps.org/watch?v=p6cgsbnnk21" style="border:0px;width:800px;height:800px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| → <math> 2 : \frac{2}{4} = 2 \cdot \frac{4}{2} = \frac{8}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 4 </math>
| |
| | |
| Auch hierbei kann schon früher gekürzt werden <math> \left(2 : \frac{2}{4} = 2 \cdot \frac{4}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{4}{1} \cdot 1 = 4 \right) </math>
| |
| | |
| |3=Merksatz}}
| |
| |2=Hilfestellung: natürliche Zahl durch einen Bruch dividieren|3=Verstecken}}
| |
| | |
| Wenn du nicht mehr weißt, wie du aus dem Bruchteil und dem Anteil das Ganze berechnen kannst, dann schaue in die nachfolgende Erklärung.
| |
| | |
| <div style="margin-left:2em">
| |
| <!--{{Lösung versteckt|1=Text zum Verstecken|2=Label fürs Anzeigen|3=Label fürs Verbergen}}-->
| |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Das Ganze stellt die Ausgangsgröße dar.<br>
| |
| Du erhältst das Ganze aus dem Bruchteil und dem Anteil indem du den Bruchteil durch den Anteil dividierst.</big><br>
| |
| <br><br> | | <br><br> |
| '''Beispiel:'''
| |
|
| |
| Julia gehören 2 Mützen für den Winter. Das sind <math>\frac{1}{3}</math> aller Mützen, die sie und ihr Bruder Marvin gemeinsam besitzen. Wie viele Mützen haben die beiden zusammen?
| |
|
| |
| Rechnung: Wir teilen 2 durch <math>\frac{1}{3}</math> und erhalten <math>2 : \frac{1}{3} = 2 \cdot \frac{3}{1} = \frac{6}{1} = 6</math>.<br>
| |
| Antwort: Den beiden gehören zusammen 6 Mützen.
| |
| |3=Merksatz}}
| |
|
| |
| |2=Erklärung: Ganze berechnen|3=Verstecken}}</div>
| |
|
| |
| {{Box|1= 5. Wie berechne ich das Ganze? [[Datei:Förderaufgabe.png|100px]] | 2=
| |
|
| |
|
| <div class="lueckentext-quiz" width="200" height="160"> | | <b>Zusammenfassung: |
| Das Ganze lässt sich mithilfe der allgemeinen Berechnungsweise '''Ganze''' = '''Bruchteil''' <math> : </math>'''Anteil''' = '''Bruchteil''' <math> \cdot </math> '''Kehrbruch des Anteils''' berechnen.
| | <br>Anteilsbestimmung von einer Größe</b> |
| Wir üben nun gemeinsam die Berechnung des Ganzen in einem gegebenen Sachzusammenhang:
| | <br> |
| | | {| class="wikitable" |
| Zu Kims Geburtstagsfeier kommen 8 Freundinnen. Das sind <math> \frac{4}{5} </math> der Freundinnen, die Kim eingeladen hat. Berechne die Anzahl der Freundinnen, die insgesamt eingeladen wurden.
| | !Brüche |
| | | !Prozente |
| Rechnung:
| | |- |
| Bruchteil = '''8''' <math> \qquad </math> Anteil= '''<math>\frac{4}{5}</math>'''
| | |Um einen bestimmten Anteil einer vorgegebenen Größe zu bestimmen, teile ich die Größe durch den Nenner des Bruchs. Anschließend multipliziere ich das Teilergebnis mit dem Zähler des Bruchs. So erhalte ich meinen gesuchten Anteil einer vorgegebenen Größe. |
| | | |<div class="lueckentext-quiz"> |
| Ganze = '''8''' <math> \cdot </math> '''<math>\frac{5}{4} </math>''' <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} </math> '''2''' <math> \cdot </math> '''<math> \frac{5}{1} </math>''' = '''10'''.
| | Um den prozentualen Anteil einer Größe zu bestimmen, teile ich die Größe durch '''100''' |
| | | Damit habe ich 1 % der Größe berechnet. Nun multipliziere ich dies mit dem gesuchten Prozentsatz. Sind z.B. 20 % gesucht, multipliziere ich mit '''20'''. So erhalte ich meinen gesuchten Anteil einer vorgegeben Größe. |
| Antwort: Kim hat zu ihrer Geburtstagsfeier 10 Freundinnen eingeladen.
| |
| </div> | | </div> |
| | |- |
| | |} |
| | <br><br> |
|
| |
|
| {{Lösung versteckt|1=
| | ==Neue Begriffe für die Prozentrechnung== |
| Das Ganze lässt sich mithilfe der allgemeinen Berechnungsweise Ganze = Bruchteil <math> : </math>Anteil = Bruchteil <math> \cdot </math> Kehrbruch des Anteils berechnen.
| |
| Wir üben nun gemeinsam die Berechnung des Ganzen in einem gegebenen Sachzusammenhang:
| |
| | |
| Zu Kims Geburtstagsfeier kommen 8 Freundinnen. Das sind <math> \frac{4}{5} </math> der Freundinnen, die Kim eingeladen hat. Berechne die Anzahl der Freundinnen, die insgesamt eingeladen wurden.
| |
| | |
| Rechnung:
| |
| Bruchteil = 8 <math> \qquad </math> Anteil= <math>\frac{4}{5}</math>
| |
| | |
| Ganze = 8 <math> \cdot </math> <math>\frac{5}{4} </math> <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} </math> 2 <math> \cdot </math> <math> \frac{5}{1} </math> = 10.
| |
| | |
| Antwort: Kim hat zu ihrer Geburtstagsfeier 10 Freundinnen eingeladen.
| |
| |2=Lösung|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| {{Box|1=6. Das Ganze berechnen|2=
| |
| | |
| Berechne nun selbst in deinem Heft das Ganze in den dargestellten Aufgaben.
| |
| | |
| Wenn du auf diesen Button [[Datei:Vollbildschirmmodus.png|30px]] in der rechten oberen Ecke klickst, dann gelangst du in den Vollbildmodus.
| |
|
| |
|
| Nachdem du alle Ganze berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe das jeweilige Ganze ziehst.
| | <b>Fülle den Lückentext mit Hilfe der Abbildung aus.</b> |
| | |
| {{LearningApp|app=pxk0w9fmj19|width=100%|height=400px}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du nicht weißt, wie du die Aufgaben lösen kannst, dann schaue dir die versteckte Erklärung vor Aufgabe 5 und die Aufgabe 5 noch einmal genau an.
| |
| |2= Tipp zum Lösen der Aufgaben|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du nicht genau weißt, wie du eine natürliche Zahl durch einen Bruch dividieren kannst oder du nicht weißt, was der Kehrbruch ist oder wie du ihn bestimmen kannst, dann schaue dir die versteckte Hilfestellung vor Aufgabe 5 noch einmal an.
| |
| |2= Hilfestellung: natürliche Zahl durch einen Bruch dividieren |3=Verstecken}}
| |
| | |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: 8 <math>\qquad</math> Anteil: <math> \frac{1}{9}</math> <br><br>
| |
| <math>8 : \frac{1}{9} = 8 \cdot \frac{9}{1} = \frac{72}{1} = 72 </math>
| |
| |2=Lösung: Aufgabe 1|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: 18 <math>\qquad</math> Anteil: <math> \frac{2}{5}</math> <br><br>
| |
| <math>18 : \frac{2}{5} = 18 \cdot \frac{5}{2} = \frac{90}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 45 </math><br><br>
| |
| oder <br><br>
| |
| <math>18 : \frac{2}{5} = 18 \cdot \frac{5}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 9 \cdot \frac{5}{1} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 45</math>
| |
| |2=Lösung: Aufgabe 2|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: 15 <math>\qquad</math> Anteil: <math> \frac{5}{9}</math> <br><br>
| |
| <math>15 : \frac{5}{9} = 15 \cdot \frac{9}{5} = \frac{135}{5} \quad \overset{\text{kürzen}}{\underset{\text{mit 5}}{=}} \quad 27 </math><br><br>
| |
| oder <br><br>
| |
| <math>15 : \frac{5}{9} = 15 \cdot \frac{9}{5} \quad \overset{\text{kürzen}}{\underset{\text{mit 5}}{=}} \quad 3 \cdot \frac{9}{1} = 27</math>
| |
| |2=Lösung: Aufgabe 3|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: 22 <math>\qquad</math> Anteil: <math> \frac{4}{6}</math> <br><br>
| |
| <math>22 : \frac{4}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 22: \frac{2}{3} = 22 \cdot \frac{3}{2} = \frac{66}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 33 </math><br><br>
| |
| oder<br><br>
| |
| <math>22 : \frac{4}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 22: \frac{2}{3} = 22 \cdot \frac{3}{2} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 11 \cdot \frac{3}{1} = 33 </math>
| |
| |2=Lösung: Aufgabe 4|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: 9 <math>\qquad</math> Anteil: <math> \frac{3}{4}</math> <br><br>
| |
| <math>9 : \frac{3}{4} = 9 \cdot \frac{4}{3} = \frac{36}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} \quad 12 </math><br><br>
| |
| oder<br><br>
| |
| <math>9 : \frac{3}{4} = 9 \cdot \frac{4}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} \quad 3 \cdot \frac{4}{1} = 12 </math>
| |
| |2=Lösung: Aufgabe 5|3=Verstecken}}
| |
| | |
| |2=Lösungen|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| ===Der Anteil ist gesucht===
| |
| | |
| | |
| In diesem Abschnitt ist immer der Bruchteil und das Ganze gegeben und es wird der Anteil gesucht.
| |
| | |
| Wenn du nicht mehr weißt, wie du aus dem Bruchteil und dem Ganzen den Anteil berechnen kannst, dann schaue in die nachfolgende Erklärung.
| |
| | |
| <div style="margin-left:2em">
| |
| <!--{{Lösung versteckt|1=Text zum Verstecken|2=Label fürs Anzeigen|3=Label fürs Verbergen}}-->
| |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Der Anteil stellt das Verhältnis zwischen dem Bruchteil und dem Ganzen dar.<br>
| |
| Er lässt sich berechnen, indem du den Bruchteil durch das Ganze dividierst.</big><br>
| |
| <br><br> | | <br><br> |
|
| |
|
| '''Beispiel:'''
| | {| class="wikitable" |
| | | ![[Datei:Kreis 2.png|506]] |
| Julia und Marvin besitzen zusammen 6 Mützen. Vier davon gehören Marvin und zwei gehören Julia. Wie groß ist der Anteil von Julias Mützen an allen Mützen der beiden?
| | !<div class="lueckentext-quiz"> |
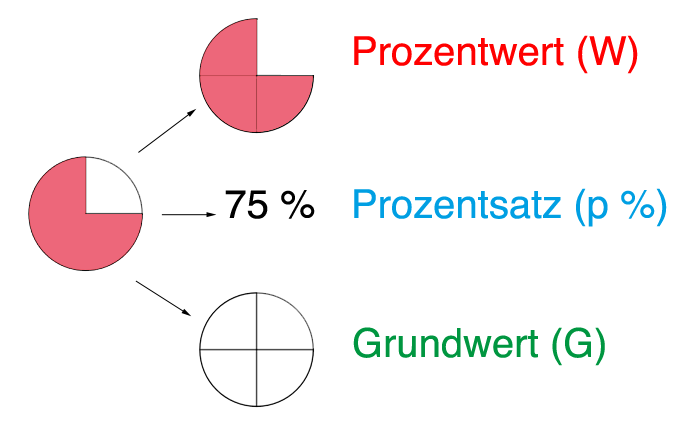
| | | In der Prozentberechnung gibt es nun andere Begriffe für das, was du bereits aus der Bruchrechnung kennst. Das Ganze heißt hier '''Grundwert''' (abgekürzt mit G). Der Teil des Ganzen bzw. der vorgegebenen Größe heißt '''Prozentwert''' (abgekürzt mit W). Der Anteil wird '''Prozentsatz''' genannt (abgekürzt p %). |
| Rechnung: Wir teilen 2 durch 6 und erhalten <math>\frac{2}{6} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{1}{3}</math>.<br>
| |
| Antwort: Julia besitzt <math>\frac{1}{3}</math> aller Mützen der beiden.
| |
| |3=Merksatz}} | |
| | |
| |2=Erklärung: Anteil berechnen|3=Verstecken}}</div>
| |
| | |
| {{Box|1= 7. Wie berechne ich den Anteil? [[Datei:Förderaufgabe.png|100px]] | 2=
| |
| | |
| <div class="lueckentext-quiz" width="200" height="160"> | |
| Der Anteil lässt sich mithilfe der allgemeinen Berechnungsweise '''Anteil''' = '''Bruchteil''':'''Ganze''' berechnen.
| |
| | |
| Wir üben nun gemeinsam die Berechnung des Anteils in einem gegebenen Sachzusammenhang:
| |
| | |
| Kim kauft für ihre Geburtstagsfeier einen Kasten mit Cola, Orangen- und Zitronenlimonade. Von den 20 Flaschen sind 10 Flaschen Cola, 6 Flaschen Orangenlimonade und vier Flaschen Zitronenlimonade. Berechne den Anteil der Zitronenlimonadenflaschen an dem gesamten Kasten.
| |
| | |
| Rechnung:
| |
| Bruchteil = '''4''' <math> \qquad </math> Ganze = '''20'''
| |
| | |
| Anteil = '''4''':'''20''' <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} </math> '''1''':'''5'''
| |
| Antwort: Der Anteil Zitronenlimonadenflaschen am gesamten Kasten beträgt <math> \frac{1}{5} </math>.
| |
| </div> | | </div> |
| | | |- |
| {{Lösung versteckt|1=
| | |} |
| Der Anteil lässt sich mithilfe der allgemeinen Berechnungsweise Anteil = Bruchteil:Ganze berechnen.
| | [[Kategorie:Algebra]] |
| | |
| Wir üben nun gemeinsam die Berechnung des Anteils in einem gegebenen Sachzusammenhang:
| |
| | |
| Kim kauft für ihre Geburtstagsfeier einen Kasten mit Cola, Orangen- und Zitronenlimonade. Von den 20 Flaschen sind 10 Flaschen Cola, 6 Flaschen Orangenlimonade und vier Flaschen Zitronenlimonade. Berechne den Anteil der Zitronenlimonadenflaschen an dem gesamten Kasten.
| |
| | |
| Rechnung:
| |
| Bruchteil = 4 <math> \qquad </math> Ganze = 20
| |
| | |
| Anteil = 4:20 <math> \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} </math> 1:5
| |
| Antwort: Der Anteil Zitronenlimonadenflaschen am gesamten Kasten beträgt <math> \frac{1}{5} </math>.
| |
| |2=Lösung|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}} | |
| | |
| {{Box|1=8. Den Anteil berechnen|2=
| |
| | |
| Berechne nun eigenständig die Anteile der dargestellten Aufgaben in deinem Heft. Kürze dabei soweit wie möglich.
| |
| | |
| Wenn du auf diesen Button [[Datei:Vollbildschirmmodus.png|30px]] in der rechten oberen Ecke klickst, dann gelangst du in den Vollbildmodus.
| |
| | |
| Nachdem du alle Anteile berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe den jeweiligen Anteil ziehst.
| |
| | |
| {{LearningApp|app=p1u95yfja19|width=100%|height=400px}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du nicht weißt, wie du die Aufgaben lösen kannst, dann schaue dir die versteckte Erklärung vor Aufgabe 7 und die Aufgabe 7 noch einmal genau an.
| |
| |2= Tipp zum Lösen der Aufgaben|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Box|1=Merke|2=
| |
| [[Bild:Comic_Merke.gif| left]]
| |
| | |
| <br>
| |
| <big>Du kannst einen Bruch kürzen, indem du den Zähler und den Nenner durch die gleiche Zahl dividierst.</big><br>
| |
| <br><br>
| |
| | |
| '''Beispiel:'''
| |
| | |
| Der Bruch <math>\frac{16}{18}</math> soll gekürzt werden. Sowohl der Zähler (16) als auch der Nenner (18) sind durch 2 teilbar.
| |
| | |
| → <math> \frac{16 : 2}{18 : 2} = \frac{8}{9} </math>
| |
| | |
| |3=Merksatz}}
| |
| |2=Hilfestellung: Kürzen|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Beachte, dass nach dem Anteil des Geldes gefragt wird, welches Mia noch benötigt. Angegeben ist mit den 280€ jedoch das Geld, welches sie schon gespart hat.
| |
| |2=Tipp: Aufgabe 2|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Beachte, dass Noah ebenfalls einen Teil der Schokolade bekommt.
| |
| |2=Tipp: Aufgabe 5|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 75 <math>\qquad</math> Bruchteil: 45 <br><br>
| |
| <math>\frac{45}{75} \quad \overset{\text{kürzen}}{\underset{\text{mit 15}}{=}} \quad \frac{3}{5} </math>
| |
| | |
| |2=Lösung: Aufgabe 1|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 360 <math>\qquad</math> Bruchteil: 360-280=80<br><br>
| |
| <math> \frac{80}{360} \quad \overset{\text{kürzen}}{\underset{\text{mit 40}}{=}} \quad \frac{2}{9} </math>
| |
| |2=Lösung: Aufgabe 2|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 26 <math>\qquad</math> Bruchteil: 8 <br><br>
| |
| <math> \frac{8}{26} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{4}{13}</math>
| |
| |2=Lösung: Aufgabe 3|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 28 <math>\qquad</math> Bruchteil: 10 <br><br>
| |
| <math> \frac{10}{28} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{5}{14} </math>
| |
| |2=Lösung: Aufgabe 4|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: 24 <math>\qquad</math> Bruchteil: 4 <br><br>
| |
| <math> \frac{4}{24} \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} \quad \frac{1}{6}</math>
| |
| |2=Lösung: Aufgabe 5|3=Verstecken}}
| |
| | |
| |2=Lösungen|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| ==Wonach ist gesucht?==
| |
| {{Box|1=9. Bruchteil, Anteil oder Ganzes berechnen?|2=
| |
| In dieser Aufgabe musst du erkennen, ob der Bruchteil, der Anteil oder das Ganze berechnet werden soll und angeben, wie dieser berechnet wird. Wähle dazu für jede Lücke die passende Möglichkeit aus.
| |
| | |
| {{LearningApp|app=pdze3kt1j19|width=100%|height=400px}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du Schwierigkeiten dabei hast zu erkennen, ob der Bruchteil, der Anteil oder das Ganze gegeben sind und was du davon berechnen sollst, dann bearbeite nochmal Aufgabe 1.
| |
| |2=Tipp: Ich weiß nicht, was berechnet werden soll|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du nicht mehr genau weißt, wie Bruchteil, Anteil oder Ganzes berechnet werden, dann schaue dir die versteckten Erklärungen vor den Aufgaben 3., 5. und 7. nochmal an.
| |
| |2=Tipp: Ich weiß nicht, wie Bruchteil, Anteil oder Ganzes berechnet wird.|3=Verstecken}}
| |
| | |
| |3= Arbeitsmethode}}
| |
| | |
| ==Teste dein neues Wissen==
| |
| | |
| Du kannst bei gegebenen Situationen erkennen, was Bruchteil, Anteil und Ganzes sind und nach welcher dieser drei Größen gefragt ist? Zusätzlich kannst du den Bruchteil, Anteil und das Ganze berechnen, wenn diese gesucht sind?
| |
| | |
| Dann teste in dem folgenden Quiz dein können und schaffe es Bruch-Millionär zu werden!
| |
| | |
| Berechne dafür die Ergebnisse auf einem Blatt Papier und kreuze die richtige Antwort an.
| |
| | |
| Viel Erfolg!
| |
| | |
| {{Box|1=10. Bruch-Millionär|2=
| |
| {{LearningApp|app=p1wgyvxdj19|width=100%|height=400px}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Wenn du Schwierigkeiten dabei hast zu erkennen, ob der Bruchteil, der Anteil oder das Ganze berechnet werden soll, dann schaue dir nochmal Aufgabe 9 genauer an.<br>
| |
| Wenn du Schwierigkeiten mit der Berechnung des Bruchteils hast, dann schaue dir nochmal die Aufgaben 3. und 4. an. <br>
| |
| Wenn du Schwierigkeiten mit der Berechnung des Ganzen hast, dann schaue dir nochmal die Aufgaben 5. und 6. an. <br>
| |
| Wenn du Schwierigkeiten mit der Berechnung des Anteils hast, dann schaue dir nochmal die Aufgaben 7. und 8. an.
| |
| |2=allgemeiner Tipp|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| {{Lösung versteckt|1=
| |
| In der Aufgabe ist der neue Preis für den Schal gesucht. Der angegebene Anteil bezieht sich jedoch auf den Rabatt, also auf den Betrag, den Liam nun nicht mehr zahlen muss.
| |
| |2=Tipp: 5.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Berechne zuerst die Anzahl an Stimmen, die Amy und Emil erhalten haben.
| |
| |2=Tipp 1: 50.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Du weißt nun, wie viele Stimmen Amy und Emil zusammen bekommen haben. Alicia hat alle anderen Stimmen erhalten.
| |
| |2=Tipp 2: 50.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| In der Aufgabe ist der Anteil des Wassers an der Schorle gesucht. Es ist jedoch nur die Menge des Saftes gegeben, der verwendet wird.
| |
| |2=Tipp 1: 1.000.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Berechne zuerst die Menge an Wasser, die für die Schorle verwendet wird.
| |
| |2=Tipp 2: 1.000.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: <math>8</math> <math>\qquad</math> Anteil: <math> \frac{4}{7} </math> <br><br>
| |
| Ganze ist gesucht:<br><br>
| |
| <math>8 : \frac{4}{7} = 8 \cdot \frac{7}{4} = \frac{56}{4} \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} \quad 14</math><br><br>
| |
| oder <br><br>
| |
| <math>8 : \frac{4}{7} = 8 \cdot \frac{7}{4} \quad \overset{\text{kürzen}}{\underset{\text{mit 4}}{=}} \quad 2 \cdot \frac{7}{1} = 14</math>
| |
| |2=Lösung: 500€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: <math>34</math> <math>\qquad</math> Bruchteil: <math>24</math> <br><br>
| |
| Anteil ist gesucht:<br><br>
| |
| <math> \frac{24}{34} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad \frac{12}{17}</math><br><br>
| |
| |2=Lösung: 1.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: <math>20</math> <math>\qquad</math> Anteil: Es gibt <math> \frac{2}{10} </math> Rabatt auf den Schal, also beträgt der noch zu zahlende Anteil <math>1-\frac{2}{10}=\frac{8}{10}</math><br><br>
| |
| Bruchteil ist gesucht:<br><br>
| |
| <math>20 \cdot \frac{8}{10} \quad \overset{\text{kürzen}}{\underset{\text{mit 2}}{=}} \quad 20 \cdot \frac{4}{5} \quad \overset{\text{kürzen}}{\underset{\text{mit 5}}{=}} \quad 4 \cdot \frac{4}{1} = 16</math><br><br>
| |
| oder <br><br>
| |
| <math>20 \cdot \frac{8}{10} \quad \overset{\text{kürzen}}{\underset{\text{mit 10}}{=}} \quad 2 \cdot \frac{8}{1} = 16</math>
| |
| |2=Lösung: 5.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: <math>24</math> <math>\qquad</math> Anteil von Amy: <math> \frac{3}{8} </math> <math>\quad</math> Anteil von Emil: <math> \frac{1}{3} </math><br><br>
| |
| Um den Bruchteil von Alicia zu berechnen, werden erst die Bruchteile von Amy und Emil berechnet und die Summe der beiden von der Gesamtanzahl der Stimmen subtrahiert. <br><br>
| |
| Bruchteil von Amy:<br><br>
| |
| <math>24 \cdot \frac{3}{8} \quad \overset{\text{kürzen}}{\underset{\text{mit 8}}{=}} \quad 3 \cdot \frac{3}{1} = 9</math><br><br>
| |
| Bruchteil von Emil: <br><br>
| |
| <math>24 \cdot \frac{1}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} 8 \cdot \frac{1}{1} = 8</math><br><br>
| |
| Zusammen haben Amy und Emil bei der Klassensprecherwahl 17 Stimmen erhalten. Alicia hat alle anderen Stimmen bekommen, daher ist der Bruchteil von Alicia: <br><br>
| |
| <math> 24-17=7</math>
| |
| |2=Lösung: 50.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Bruchteil: <math>140+70=210 </math> <math>\qquad</math> Anteil: <math> \frac{3}{7} </math> <br><br>
| |
| Ganze ist gesucht:<br><br>
| |
| <math>210 : \frac{3}{7} = 210 \cdot \frac{7}{3} \quad \overset{\text{kürzen}}{\underset{\text{mit 3}}{=}} \quad 70 \cdot \frac{7}{1} = 490 </math><br><br>
| |
| |2=Lösung: 250.000€-Frage|3=Verstecken}}
| |
| | |
| {{Lösung versteckt|1=
| |
| Ganze: <math>390</math> <math>\qquad</math> Bruchteil: <math>390-70-50=270</math> <br><br>
| |
| Anteil ist gesucht:<br><br>
| |
| <math> \frac{270}{390} \quad \overset{\text{kürzen}}{\underset{\text{mit 30}}{=}} \quad \frac{9}{13}</math><br><br>
| |
| |2=Lösung: 1.000.000€-Frage|3=Verstecken}}
| |
| | |
| |2=Lösungen|3=Verstecken}}
| |
| | |
| |3=Arbeitsmethode}}
| |