Integralrechnung/Vorüberlegungen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Dickesen Keine Bearbeitungszusammenfassung |
Main>Dickesen Keine Bearbeitungszusammenfassung |
||
| Zeile 37: | Zeile 37: | ||
{{Merke-M| | {{Merke-M| | ||
Allgemein berechnet sich eine solche aus Rechtecks- und Dreiecksfläche zusammengesetzte Fläche natürlich nach der Formel <math>A = a \cdot b + \frac{1}{2} \cdot h \cdot b</math>, wenn <math>a</math> die Höhe des Rechtecks, <math>h</math> die Höhe des Dreiecks und <math>b</math> die Breite des Dreiecks bzw. Rechtecks sind. <br> | Allgemein berechnet sich eine solche aus Rechtecks- und Dreiecksfläche zusammengesetzte Fläche natürlich nach der Formel <math>A = a \cdot b + \frac{1}{2} \cdot h \cdot b</math>, wenn <math>a</math> die Höhe des Rechtecks, <math>h</math> die Höhe des Dreiecks und <math>b</math> die Breite des Dreiecks bzw. Rechtecks sind. <br> | ||
Diese Summe aus den beiden Einzelflächen kann nun interpretiert werden als der Mittelwert der | Diese Summe aus den beiden Einzelflächen kann nun interpretiert werden als der Mittelwert der unteren Rechtecksfläche und der oberen Rechtecksfläche! <br> | ||
[[Bild:Flaeche_mittelwert.png|zentriert|350px]] | |||
}} | }} | ||
}}}} | }}}} | ||
Version vom 16. Oktober 2009, 12:37 Uhr
Frage
Aber wie kann man diesen Flächeninhalt denn nun genau bestimmen bzw. berechnen?
Dies ist die zentrale Frage des vorliegenden Lernpfades!
Um der Lösung näher zu kommen, fangen wir mit einfachen und sehr speziellen Graphen von Funktionen an und arbeiten uns ausgehend davon immer weiter hin zu schwierigeren und allgemeineren Graphen von Funktionen, damit wir am Ende eine Lösung für alle Eventualitäten in Händen halten!
Vorlage:Aufgaben-M
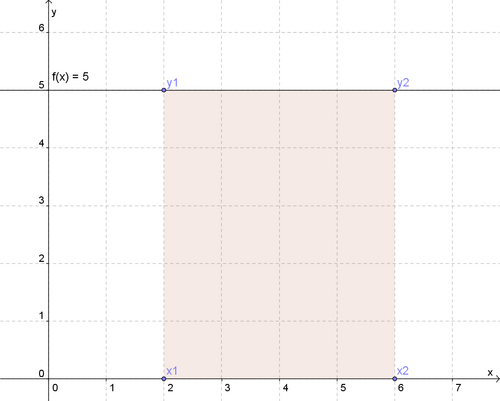
a) Konstante Funktion: in den Grenzen und
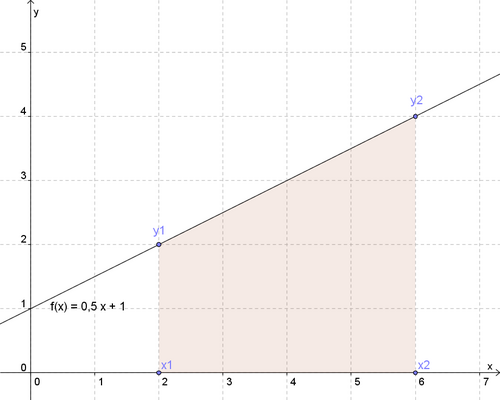
b) Lineare, nicht-konstante Funktion: in den Grenzen und
