Integralrechnung: Unterschied zwischen den Versionen
Main>Nic3381 (table+) |
Main>Nic3381 Keine Bearbeitungszusammenfassung |
||
| Zeile 70: | Zeile 70: | ||
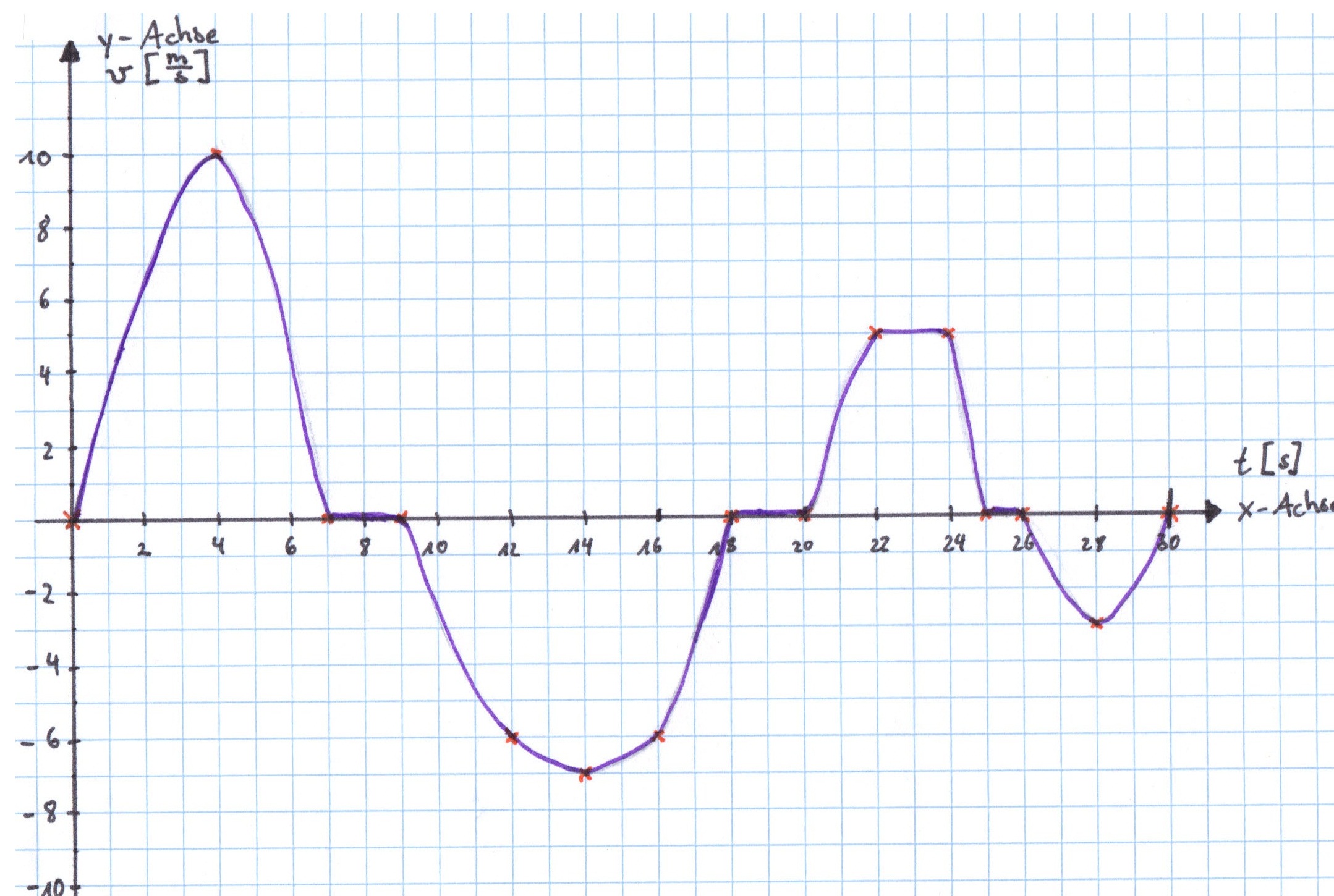
a) '''Skizziere den Graphen der Geschwindigkeits-Zeit-Funktion der Rangierlok!'''<br> | a) '''Skizziere den Graphen der Geschwindigkeits-Zeit-Funktion der Rangierlok!'''<br> | ||
{{Lösung versteckt|[[Datei:Nic3381_Rangierlok3.JPG]]}}<br><br> | {{Lösung versteckt|[[Datei:Nic3381_Rangierlok3.JPG]]}}<br><br> | ||
b) In welchen Zeitabschnitten bewegt sich | b) '''In welchen Zeitabschnitten bewegt sich die Lok vorwärts bzw. rückwärts?''' <br> | ||
{{Lösung versteckt|{{Lösung|Bewegung | {{Lösung versteckt|{{Lösung|Bewegung vorwärts wenn der Graph oberhalb der x-Achse liegt für | ||
<math>0 \leq t \leq | <math>0 \leq t \leq 7</math> und <math>20 \leq t \leq 25.</math> <br> <br> | ||
Bewegung | Bewegung rückwärts wenn der Graph unterhalb der x-Achse liegt für | ||
<math>9 \leq t \leq | <math>9 \leq t \leq 18</math> und <math>26 \leq t \leq 30.</math> | ||
}}}} | }}}} | ||
c) Wann hat | c)''' Wann hat die Lok die größte Geschwindigkeitvorwärts bzw. rückwärts erreicht?''' <br> | ||
{{Lösung versteckt|{{Lösung|Größte Geschwindigkeit | {{Lösung versteckt|{{Lösung|Größte Geschwindigkeit vorwärts am Hochpunkt des Graphen für <math>t = 4.</math> <br> | ||
Größte Geschwindigkeit | Größte Geschwindigkeit rückwärts am Tiefpunkt des Graphen für <math>t = 14.</math> | ||
}}}} | }}}} | ||
d) '''Wann wird die Lok schneller, wann wird sie langsamer?''' <br> | |||
{{Lösung versteckt|{{Lösung| | {{Lösung versteckt|{{Lösung| | ||
Bewegung | Bewegung '''vorwärts''': <br> | ||
Lok wird schneller bei positiver Steigung des Graphen: <math>0 \leq t \leq 4 \ ; \ 20 \leq t \leq 22</math> <br> | |||
Lok wird langsamer bei negativer Steigung des Graphen: <math>4 \leq t \leq 7 \ ; \ 22 \leq t \leq 25</math> | |||
<br><br> | <br><br> | ||
Bewegung | Bewegung '''rückwärts''': <br> | ||
Lok wird schneller bei negativer Steigung des Graphen: <math>9 \leq t \leq 14 \ ; \ 26 \leq t \leq 28</math> <br> | |||
Lok wird langsamer bei positiver Steigung des Graphen: <math>14 \leq t \leq 18 \ ; \ 28 \leq t \leq 30</math> | |||
}}}} | }}}} | ||
e) Gib eine Schätzung für die Breite des | e)''' Gib eine Schätzung für die Breite des Rangierbahnhofes an unter der Voraussetzung, dass die Lok zum Zeitpunkt t = 7 das Endsignal und somit die Grundstücksgrenze erreicht hat.''' <br> | ||
{{Lösung versteckt|{{Lösung| | {{Lösung versteckt|{{Lösung| | ||
Strecke | Strecke vom mittleren Signal bis zu den beiden Rändern jeweils ca. 35m. <br> | ||
Somit ergibt sich eine Grundstücksbreite von ca. | Somit ergibt sich eine Grundstücksbreite von ca. 70m. | ||
}}}} | }}}} | ||
f) Im letzten Aufgabenteil hast Du ausgehend von der | f)''' Im letzten Aufgabenteil hast Du ausgehend von der von der Lok zurückgelegten Strecke die Bahnhofsbreite geschätzt. Woran kann man die zurückgelegte Strecke in obigem Diagramm erkennen?''' <br> | ||
{{Lösung versteckt|{{Lösung| | {{Lösung versteckt|{{Lösung| | ||
Die zurückgelegte Strecke zeigt sich im Diagramm als Fläche zwischen dem Graphen und der x-Achse. <br> Dabei ist die zurückgelegte Strecke | Die zurückgelegte Strecke zeigt sich im Diagramm als Fläche zwischen dem Graphen und der x-Achse. <br> Dabei ist die zurückgelegte Strecke vorwärts die Fläche zwischen dem Graphen und der x-Achse ''oberhalb'' der x-Achse und die zurückgelegte Strecke rückwärts ist die Fläche zwischen dem Graphen und der x-Achse ''unterhalb'' der x-Achse! | ||
}}}} | }}}} | ||
g) Befindet sich | g) '''Befindet sich die Lok nach 30 Sekunden vor oder hinter dem mittleren Signal?''' <br> | ||
{{Lösung versteckt|{{Lösung| | {{Lösung versteckt|{{Lösung| | ||
Da der Flächeninhalt zwischen dem Graphen und der x-Achse ''oberhalb'' der x-Achse etwas größer ist als derjenige ''unterhalb'' der x-Achse, befindet sich | Da der Flächeninhalt zwischen dem Graphen und der x-Achse ''oberhalb'' der x-Achse etwas größer ist als derjenige ''unterhalb'' der x-Achse, befindet sich die Lok vor dem mittleren Signal. | ||
}}}} | }}}} | ||
<br><br><br> | <br><br><br> | ||
Version vom 9. November 2012, 16:26 Uhr
kleine Einführung in die Integralrechnung
Vorlage:Lernpfad-M
Vorlage:Kasten blau
So, jetzt kann es endlich losgehen.
Vorlage:Aufgaben-M
Die Lok startet zur Zeit t = 0 am Mittleren Signal.
| Zeit t[s] | Geschwindigkeit v[m/s] |
|---|---|
| 0 | 0 |
| 4 | 10 |
| 7 | 0 |
| 9 | 0 |
| 12 | -6 |
| 14 | -7 |
| 16 | -6 |
| 18 | 0 |
| 20 | 0 |
| 22 | 5 |
| 24 | 5 |
| 26 | 0 |
| 28 | -3 |
| 30 | 0 |
Bearbeite die folgenden Aufgaben und begründe Deine Antwort:
a) Skizziere den Graphen der Geschwindigkeits-Zeit-Funktion der Rangierlok!
b) In welchen Zeitabschnitten bewegt sich die Lok vorwärts bzw. rückwärts?
c) Wann hat die Lok die größte Geschwindigkeitvorwärts bzw. rückwärts erreicht?
d) Wann wird die Lok schneller, wann wird sie langsamer?
e) Gib eine Schätzung für die Breite des Rangierbahnhofes an unter der Voraussetzung, dass die Lok zum Zeitpunkt t = 7 das Endsignal und somit die Grundstücksgrenze erreicht hat.
f) Im letzten Aufgabenteil hast Du ausgehend von der von der Lok zurückgelegten Strecke die Bahnhofsbreite geschätzt. Woran kann man die zurückgelegte Strecke in obigem Diagramm erkennen?
g) Befindet sich die Lok nach 30 Sekunden vor oder hinter dem mittleren Signal?
Vorlage:Navigation Lernpfad eine kleine Einführung in die Integralrechnung