Bruchteile bestimmen

Lernpfad: Bruchteile bestimmen

 Arbeitsblatt - Komplette Lösung zum Arbeitsblatt

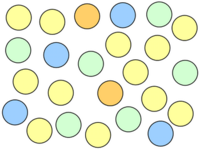
Bestimme den Anteil der gelben, blauen, grünen und orangenen Kringel!

Hilfe: Grundwissen

Bruchteile

: $\frac{1}{2}$; : $\frac{1}{6}$; : $\frac{1}{4}$; : $\frac{1}{12}$

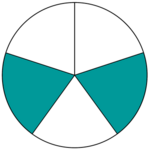
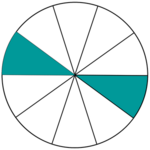
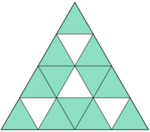
Welcher Anteil der Figur ist gefärbt?

Überlege dir: Wieviele gleich große Teile hat die Figur? Wie viele davon sind gefärbt?

Hilfe

3 von 6 Teilen sind gefärbt

Bruchteil

$\frac{1}{2}$

Hilfe

2 von 8 Teilen sind gefärbt

Bruchteil

$\frac{1}{4}$

Hilfe

2 von 5 Teilen sind gefärbt

Bruchteil

$\frac{2}{5}$

Hilfe

2 von 10 Teilen sind gefärbt

Bruchteil

$\frac{1}{5}$

Hilfe

3 von 6 Teilen sind gefärbt

Bruchteil

$\frac{1}{2}$

Hilfe

12 von 16 Teilen sind gefärbt

Bruchteil

$\frac{3}{4}$

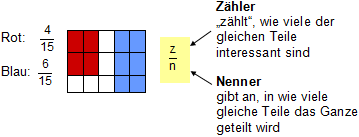
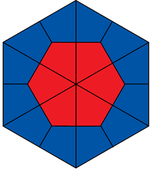
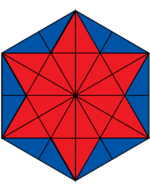
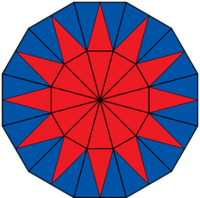
Welcher Bruchteil der Figur ist rot gefärbt?

Überlege dir eine sinnvolle Einteilung der Figur in gleich große Teile! Du findest alle Figuren auf  diesem Blatt zum Download.

Hilfe

Bruchteil

$\frac{1}{3}$

Hilfe

Bruchteil

$\frac{2}{3}$

Hilfe

Bruchteil

$\frac{1}{4}$

schwer

Hilfe

Bruchteil

$\frac{1}{2}$

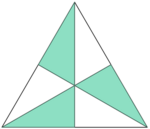
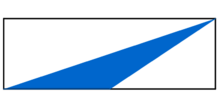
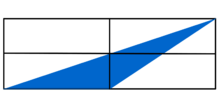
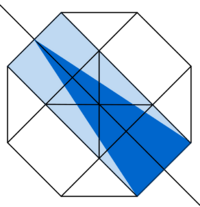
Welcher Bruchteil der Figur ist blau gefärbt?

Hilfe

Bruchteil

$\frac{1}{4}$

Hinweis zu alternativer Lösung

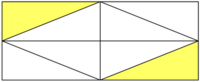
Wie verändert sich die Fläche des blauen Dreiecks, wenn die obere Ecke nach links verschoben wird?

schwer

Hilfe 1

Hilfe 2

Bruchteil

$\frac{1}{4}$

Hinweis zu alternativer Lösung

Wie verändert sich die Fläche des blauen Dreiecks, wenn die Höhe halbiert wird? Lässt sich zu solch einem Dreieck die Fläche durch Symmetrieüberlegungen finden?

Weiter zu: Grundwissen Brüche

Autoren: Maria Eirich, Andrea Schellmann <metakeywords>ZUM2Edutags,ZUM-Wiki,Bruchteile bestimmen,Mathematik-digital, Lernpfad, Bruch, Brüche, Bruchrechnung, interaktive Übungen, Mathematik, 6. Klasse, Sekundarstufe 1</metakeywords>