Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Bruchteile bestimmen/Lösung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Maria Eirich (fehler ausgebessert) |
Main>Matthias Scharwies K (<popup>) |
||
| Zeile 53: | Zeile 53: | ||
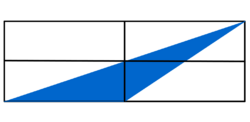
|<math>\frac{1}{4} </math>, denn schiebt man in der rechten Figur bei den kleinen Rechtecken das rechte, untere Rechteck nach rechts und dreht das rechte, obere Rechteck um 180° um die linke, untere Ecke, dann wird das linke, untere Rechteck vollständig mit blauen "Dreiecks-Puzzle-Teilen" ausgefüllt. | |<math>\frac{1}{4} </math>, denn schiebt man in der rechten Figur bei den kleinen Rechtecken das rechte, untere Rechteck nach rechts und dreht das rechte, obere Rechteck um 180° um die linke, untere Ecke, dann wird das linke, untere Rechteck vollständig mit blauen "Dreiecks-Puzzle-Teilen" ausgefüllt. | ||
|} | |} | ||
<popup name="Alternative Lösung">Die Fläche des blauen Dreiecks ändert sich nicht, wenn man die obere Ecke ganz nach links in das Rechteck "schiebt". Dies folgt aus der Flächenformel <math>A_{Dreieck}=\frac{1}{2} \cdot g \cdot h </math>. Damit ist aber klar, dass dieses Dreieck die Hälfte der linken Rechtecksseite einnimmt - also ein Viertel der gesamten Rechtecksfläche.</popup> | |||
{| border="0" | {| border="0" | ||
! width="50" | | ! width="50" | | ||
| Zeile 67: | Zeile 67: | ||
|<math>\frac{1}{4} </math> | |<math>\frac{1}{4} </math> | ||
|} | |} | ||
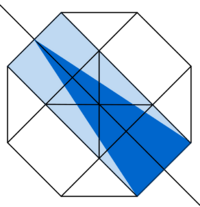
<popup name="Alternative Lösung">Die Fläche des blauen Dreiecks halbiert sich, wenn man die Höhe halbiert. Dies folgt aus der Flächenformel <math>A_{Dreieck}=\frac{1}{2} \cdot g \cdot h </math>. Die Spitze eines solchen Dreieck liegt genau in der Mitte der Figur. Aus Symmetriegründen ist die Fläche solch eines Dreieck genau ein Achtel der Gesamtfläche. Damit muss die ursprüngliche blaue Fläche ein Viertel der Gesamtfläche betragen.}</popup> | |||
[[Mathematik-digital/Grundwissen - Brüche|Grundwissen Brüche]] | [[Mathematik-digital/Grundwissen - Brüche|Grundwissen Brüche]] | ||
Version vom 16. Januar 2018, 16:40 Uhr
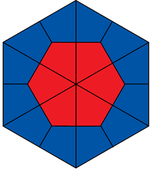
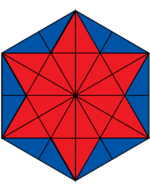
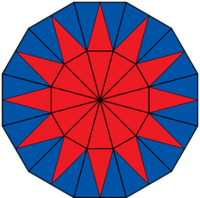
Lösung: Welcher Bruchteil ist rot gefärbt?
| Lösungshilfe | |||
|---|---|---|---|
| Etwas schwerer |
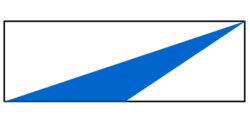
Lösung: Welcher Bruchteil ist blau gefärbt?
| , denn schiebt man in der rechten Figur bei den kleinen Rechtecken das rechte, untere Rechteck nach rechts und dreht das rechte, obere Rechteck um 180° um die linke, untere Ecke, dann wird das linke, untere Rechteck vollständig mit blauen "Dreiecks-Puzzle-Teilen" ausgefüllt. |
<popup name="Alternative Lösung">Die Fläche des blauen Dreiecks ändert sich nicht, wenn man die obere Ecke ganz nach links in das Rechteck "schiebt". Dies folgt aus der Flächenformel . Damit ist aber klar, dass dieses Dreieck die Hälfte der linken Rechtecksseite einnimmt - also ein Viertel der gesamten Rechtecksfläche.</popup>
| Zum Knobeln |
<popup name="Alternative Lösung">Die Fläche des blauen Dreiecks halbiert sich, wenn man die Höhe halbiert. Dies folgt aus der Flächenformel . Die Spitze eines solchen Dreieck liegt genau in der Mitte der Figur. Aus Symmetriegründen ist die Fläche solch eines Dreieck genau ein Achtel der Gesamtfläche. Damit muss die ursprüngliche blaue Fläche ein Viertel der Gesamtfläche betragen.}</popup>