Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Bruchteile bestimmen/Lösung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Kuddelmuddel |
Main>Kuddelmuddel |
||
| Zeile 51: | Zeile 51: | ||
|[[Bild:Bruchteile6 lös wiki.png|250px|centre]] | |[[Bild:Bruchteile6 lös wiki.png|250px|centre]] | ||
|<math>\frac{1}{4} </math> | |<math>\frac{1}{4} </math>, denn schiebt man in der rechten Figur bei den kleinen Rechtecken das rechte, untere Rechteck nach rechts und dreht das rechte, obere Rechteck um 180° um die linke, untere Ecke, dann wird das linke, untere Rechteck vollständig mit blauen "Dreiecks-Puzzle-Teilen" ausgefüllt. | ||
|} | |} | ||
'''Alternative Lösung''' {{versteckt|Die Fläche des blauen Dreiecks ändert sich nicht, wenn man die obere Ecke ganz nach links in das Rechteck "schiebt". Dies folgt aus der Flächenformel <math>A_{Dreieck}=\frac{1}{2} \cdot g \cdot h </math>. Damit ist aber klar, dass dieses Dreieck die Hälfte der linken Rechtecksseite einnimmt - also ein Viertel der gesamten Rechtecksfläche.}} | |||
{| border="0" | {| border="0" | ||
! width="50" | | ! width="50" | | ||
Version vom 14. Januar 2008, 10:55 Uhr
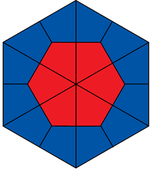
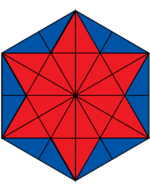
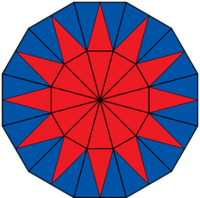
Lösung: Welcher Bruchteil ist rot gefärbt?
| Lösungshilfe | |||
|---|---|---|---|
| Etwas schwerer |
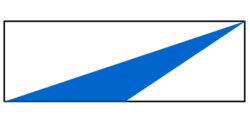
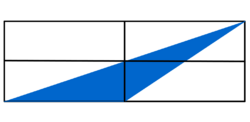
Lösung: Welcher Bruchteil ist blau gefärbt?
| , denn schiebt man in der rechten Figur bei den kleinen Rechtecken das rechte, untere Rechteck nach rechts und dreht das rechte, obere Rechteck um 180° um die linke, untere Ecke, dann wird das linke, untere Rechteck vollständig mit blauen "Dreiecks-Puzzle-Teilen" ausgefüllt. |
Alternative Lösung Vorlage:Versteckt
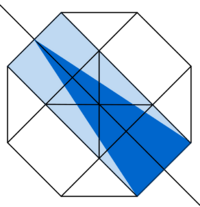
| Zum Knobeln |
Alternative Lösung Vorlage:Versteckt