Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen
Main>Jan Wörler |
Main>Jan Wörler |
||
| Zeile 120: | Zeile 120: | ||
<!--<ggb_applet height="400" width="400" showMenuBar="false" showResetIcon="true" filename="rosette.ggb" />--> | <!--<ggb_applet height="400" width="400" showMenuBar="false" showResetIcon="true" filename="rosette.ggb" />--> | ||
<br /> | <br /> | ||
| Zeile 130: | Zeile 129: | ||
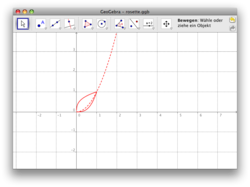
[[Bild:rosette_1.png|thumb|right|250px|Das erste Blatt setzt sich aus drei abschnittsweise definierten Potenzfuntktionen zusammen.]] | [[Bild:rosette_1.png|thumb|right|250px|Das erste Blatt setzt sich aus drei abschnittsweise definierten Potenzfuntktionen zusammen.]] | ||
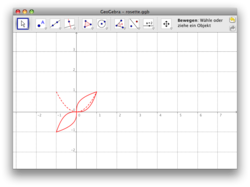
[[Bild:rosette_2.png|thumb| | [[Bild:rosette_2.png|thumb|rahmenlos|right|250px]] | ||
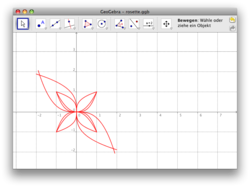
[[Bild:rosette_3.png|thumb|frameless|right|250px| asdasd]] | [[Bild:rosette_3.png|thumb|frameless|right|250px| asdasd]] | ||
Version vom 2. Februar 2009, 15:56 Uhr
Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN
Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form mit als Exponenten haben. Für diese Art der Exponenten gilt: .
Vergleich mit Funktionen aus Stufe 3
| Vorlage:Arbeiten |
Die Datei [INVALID] wurde nicht gefunden. |
Exponenten, Brüche und Potenzgesetze
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponten. Man erinnere sich dabei an die Potenzgesetze, insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl und eine natürliche Zahl wird definiert:
- für
Auf unsere Situation angewandt ergibt sich:
| Vorlage:Arbeiten |
Potenzfunktionen und ihre Umkehrfunktionen
Beispiel
| Es sei eine Potenzfunktion, definiert durch . Gesucht ist die Umkehrfunktion von .
ergibt sich aus durch Auflösen nach . Es ist: Vertauschen von und ergibt schließlich die gesuchte Funktion: . |
Die Datei [INVALID] wurde nicht gefunden. |
Beispiel
| Es sei eine Potenzfunktion, nun definiert durch mit Definitionsbereich ID = IR+. Gesucht ist wieder ihre Umkehrfunktion .
Auflösen nach ergibt: |
Die Datei [INVALID] wurde nicht gefunden. |
Hinweis: man beachte besonders hier die unterschiedliche Bedeutung von und !
Vergleich mit Potenzfunktionen der Stufe 1
Im Zusammenhang mit den Umkehrfunktionen dieser Art kann es sinnvoll sein, sich die Potenzfunktionen der Stufe 1 noch einmal vor Augen zu führen. Hier kannst Du direkt zur Stufe 1 springen.
Zusammenfassung
Die Umkehrfunktionen von Potenzfunktionen der Bauart mit sind Potenzfunktionen der Bauart
Die Umkehrfunktionen von Potenzfunktionen der Bauart mit sind Potenzfunktionen der Bauart .
Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"
- Spiegeln
- Strecken
- Stauchen
- Schieben
- Superponieren
Siehe Video auf www.oberprima.com.
APPLET
Die Datei [INVALID] wurde nicht gefunden.
Mit Funktionen malen
Das nebenstehende Bild ist vollständig aus Potenzfunktionen der Form
mit zusammengesetzt. Bearbeite zu dem Bild nacheinander folgende Fragen: