Kongruenz von Dreiecken

Einleitung

Ein Lernpfad ist eine Möglichkeit, bei der du den Computer als Lernhilfe benutzt. Dich erwarten in diesem Lernpfad neue mathematische Inhalte über Dreiecke und Abbildungen, die du selbstständig nacheinander erlernst. Gehe die einzelnen Kapitel von oben nach unten durch. Jeder Schritt beginnt mit einer Einführungsaufgabe, bei der du probieren, knobeln und entdecken kannst. Es folgen Aufgaben in verschiedenen Schwierigkeitsstufen:

leichte Aufgabe

normale Aufgabe

schwierigere Aufgabe

Einige Übungen kannst du auch mit deinem Schulbuch bearbeiten. Ich wünsche dir beim Entdecken und Lernen viel Spass!

Solltest du irgendwo Probleme haben, so schau dir diese Erklärungen noch einmal an, oder gehe eventuell einen Schritt auf dem Lernpfad zurück.

Einstieg ins Thema

Damit du mit dem dich erwartenden Thema etwas vertraut wirst, bearbeite mindestens zwei der Einstiegsübungen!

1. Ein Smiley kommt selten allein!

Im folgenden Bild sind verschiedene Smileys gleich. Finde sie und erkläre deinem Partner, wie du zu deiner Entscheidung gekommen bist!

<popup> </popup>

Die Lösung findest du am Lehrertisch.

2. Der Schlangenbeschwörer!

In dieser Bilderfolge sind zwei Bilder gleich. Finde sie und erkläre deinem Partner, wie du zu deiner Entscheidung gekommen bist!

<popup></popup>

Die Lösung findest du am Lehrertisch.

3. Schule als Puzzle!

Finde die richtigen Puzzleteile! Erkläre, wie du sie herausgefunden hast!
<popup>Datei:Puzzle Gebäude.png</popup>

Die Lösung findest du am Lehrertisch.

4. Verflixte Zweige!

Nur in zwei Kästchen sind die Zweige völlig gleich. Gib die Koordinaten dieser Kästchen an und beschreibe deinem Partner deine Strategie!
<popup></popup>

Die Lösung findest du am Lehrertisch.

Aufgabe

Schreibe in deine Lernmappe, mit welcher Vorgehensweise du die Aufgaben gelöst hast! Lasse dir dann den Merksatz anzeigen und trage ihn in deine Lernmappe an der richtigen Stelle ein!

Merke

<popup> Zwei Figuren A und B, die in Größe und Form übereinstimmen, heißen kongruent zueinander. Man sagt auch, sie sind deckungsgleich. Zur Abkürzung schreibt man: A Datei:Kongruenzzeichen.png B.

</popup>

Wofür braucht man Kongruenz?

Kongruente Figuren haben nicht nur etwas mit Suchspielen zu tun, sondern spielen auch in deinem Alltag eine wichtige Rolle, z.B. beim Vergleichen von Fingerabdrücken, um einen Verdächtigen zu überführen oder in der Architektur.

Aufgabe

Suche dir ein Gebäude aus! Erkläre deinem Nachbarn, wo du kongruente Teilfiguren entdeckst!

• 

  Staatstheater in Mainz

• 

  Landtag in Mainz

Auch haben sich viele Mathematiker mit der Kongruenz von Figuren beschäftigt. Sie sind dabei auf viele erstaunliche und interessante Ergebnisse gekommen. Einige wirst du nun kennenlernen.

Kongruenz, das Gleichheitszeichen der Geometrie!

Unterrichtsidee

Überlege dir, wo in deinem täglichen Leben kongruente Figuren wichtig sind! Hast du einen Vorschlag für eine gute Aufgabe, an der man kongruente Figuren gut erkennt?

Datei:Vorstellung Kongru und Enz 2.png

Pauls Zimmerwand

Aufgabe

Peter hat seine Zimmerwand mit einem bunten Muster aus kongruenten Dreiecken gestaltet. Sie sieht nun so aus: <popup></popup>

Leider war die Sprechblase für Peter nicht groß genug. Aber du kannst dir bestimmt denken, wie er es gemacht hat. Du kannst es entweder zuerst in deiner Lernmappe oder mit Geogebra versuchen GeoGebra-Datei die Wand von Peter zu gestalten. Dir fallen bestimmt mehrere Möglichkeiten ein, um die Wand mit Dreiecken zu füllen. Schreibe sie unter deine Zeichnung. Zeige die Zeichnung deinem Lehrer!

Die geometrischen Abbildungen helfen dir.

Überlege dir, welcher Zusammenhang zwischen geometrischen Abbildungen und dem Begriff der Kongruenz besteht!

Übernimm den Merksatz in deine Lernmappe!

Merke

<popup>Achsenspiegelung, Punktspiegelung, Drehung und Verschiebung führen Figuren in kongruente Figuren über. Man nennt sie daher auch Kongruenzabbildungen.</popup>

Löse folgende Aufgabe mit Geogebra.

Aufgabe

Auch Peter besucht in der Schule den Mathematikunterricht. Er hat diese Aufgabe gestellt bekommen.

<popup></popup>

Bei einer Gruppenarbeit ist folgendes zu hören:

Tobias: Ich habe in meinem Geometrieprogramm das Dreieck ABC verschoben, dann das Bilddreieck um einen Punkt gedreht und so das Dreieck DEF erhalten.

Laura: Ich habe es genau andersrum wie Tobias gemacht.

Miriam: Ich habe nur an Achsen gespiegelt.

Peter: Ihr könntet alle Recht haben! Wir müssen es ausprobieren.

Versetze dich in Lage von Peter und experimentiere.

GeoGebra-Datei mit Hilfe GeoGebra-Datei ohne Hilfe

Übernimm die Aufgabenstellung auf ein karriertes Blatt. Zeichne mindestens zwei Lösungen in unterschiedlicher Farbe mit Geodreieck und Zirkel.

Drei Seiten, ein Dreieck?

Aufgabe

Peter hat als Hausaufgabe diesen Auftrag bekommen. Er fragt seine Eltern um Rat, doch diese können ihm keinen gute Idee geben. Er versucht Informationen für eine Lösung im Internet zu finden und stößt dabei auf einen Lernpfad: Drei Seiten ein Dreieck
Peter bearbeitet in diesem Lernpfad die Aufgaben zum Thema "Drei Seiten ein Dreieck?". Auf einem Arbeitsblatt in seiner Lernmappe notiert er, was er bei den einzelnen Teilaufgaben gelernt hat.

Mache es genauso wie Peter!

Merke

Ein Dreieck ist genau dann aus drei Seitenlängen konstruierbar, wenn
<popup>die Summe aus zwei Dreiecksseiten stets größer als die Länge der dritten Seite ist:

c < a + b oder b < a + c oder a < c + b.</popup>

Teste dich!

Löse das Schüttelrätsel und überprüfe dein Wissen!

Zwei Figuren sind kongruent wenn sie in Form und Größe übereinstimmen. Mit den kongruenten Abbildungen: Achsenspiegelung, Verschiebung,Punktspiegelung und Drehung können wir zeigen, dass Orginalfigur und Bildfigur genau übereinander passen. Kongruente Figuren sind also deckungsgleich.

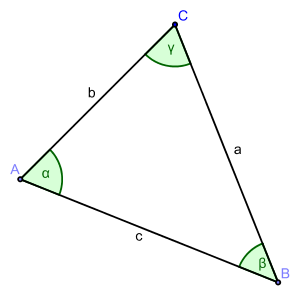
Stimmen zwei Dreiecke ABC und A´B´C´ in allen drei Winkel-größen und den drei Seiten-längen überein, so sagt man ebenfalls, sie sind kongruent.

Kongruenzüberprüfungen für Schnelltester

Peter musste am Ende der letzten Mathestunde unbedingt mit Paul besprechen, wer sich in der Pause um die Organisation des nächsten Fußballspiels kümmert, deshalb hat er leider die Hausaufgabe nicht mitbekommen. Nun telefoniert er mit Lisa: "Wir sollen alle kongruente Dreieck konstruieren." Sie misst eine Weile, dann sagt sie: "Und zwar soll a= 5cm, b=12cm, c=13cm, $\alpha$= 27,3°,$\beta$=62,7°, $\gamma$=90° sein."

"Meine Güte!" meint Peter, "Geht es nicht kürzer? Muss ich wirklich alle Seitenlängen und alle Winkelgrößen wissen, damit ich ein Dreieck konstruieren kann, das kongruent zu deinem ist?" "Mach doch was du willst." entgegnet Lisa beleidigt. "Dann konstruier doch ein Dreieck aus der Seite a und b. Alles andere kannst du ja weglassen. Mir ist doch egal, wenn du ein falsches Dreieck hast!"

Aufgabe

Was meinst du? Braucht man alle Angaben? Genügen zwei Streckenlängen? Probiere es aus! Du kannst sowohl per Hand als auch mit Geogebra GeoGebra-Datei arbeiten. Hätte Lisa Möglichkeiten gehabt, Peter mit weniger, aber ausreichnd Informationen zu versorgen?

Benutze zur Bearbeitung die Tabelle in deiner Lernmappe!

Kontrolle deiner Ergebnisse

<popup name="Lösung"> Sind von einem Dreieck drei Größen bekannt, lässt es sich häufig eindeutig konstruieren. D.h. es ist bis auf die Lage festgelegt. Eine der drei Größen muss eine Seite sein. </popup>

Kongruenzsätze zur eindeutigen Konstruktion von Dreiecken

Merke

Hier steht S für eine Seite, W für einen Winkel.
SSS: <popup>Stimmen zwei Dreiecke in den drei __________ überein, so sind sie zueinander kongruent. </popup>

SWS: <popup>Stimmen zwei Dreiecke in zwei __________ und dem __________ Winkel überein, so sind sie zueinander kongruent.</popup>

WSW: <popup>Stimmen zwei Dreiecke in einer __________ und den zwei __________ Winkeln überein, so sind sie zueinander kongruent.</popup>

SsW: <popup>Stimmen zwei Dreiecke in __________ Seiten und dem der größten Seite __________ Winkel überein, so sind sie kongruent.</popup>

Dreiecke eindeutig konstruieren

Im folgenden probiert Peter zu jedem Konstruktionssatz ein eindeutiges konstruierbares Dreieck zu erstellen! Sie dir die einzelnen Konstruktionsfilme an. Fertige dann eine Konstruktionsbeschreibung an!

Konstruktionsfilm zu SSS

Konstruktionsfilm zu SWS

Konstruktionsfilm zu WSW

Konstruktionsfilm zu SsW

Teste Dich

Kongruenzsätze
Finde die Paare aus je einem Bild und dem dazu passenden Begriff.

Bringe die Konstruktionsschritte in die richtige Reihenfolge

	Konstruktionsbeschreibung SSS.	Konstruktionsbeschreibung SWS.	Konstruktionsbeschreibung WSW.	Konstruktionsbeschreibung SsW.
geg.:	a=4,5cm, b=5,2cm, c=7,1cm	b=6,5cm, c=4,2cm, $\alpha$=70°	c=5,7cm $\alpha$=40°,$\beta$=78°	b=3cm,a=3 cm, $\gamma$=87°
1.	Die Strecke $\overline { AB }$ =7,1 cm zeichnen.	Die Strecke $\overline { AB }$ =4,2 cm zeichnen.	Die Strecke $\overline { AC }$ =5,7 cm zeichnen.	Die Strecke $\overline { BC }$ =3 cm zeichnen.
2.	Kreisbogen um A mit Radius b=5,2cm zeichnen.	In A den Winkel $\alpha$=70° antragen.	In A den Winkel $\alpha$=40° antragen.	In C den Winkel $\gamma$=87° antragen.
3.	Kreis um B mit Radius a=4,5cm zeichnen.	Kreis um A mit Radius b=6,5cm zeichnen	In B den Winkel $\beta$=78° antragen.	Kreis um C mit Radius b=3cm zeichnen.
4.	Den Schnittpunkt der Kreise mit C benennen.	Den Schnittpunkt C eintragen.	Den Schnittpunkt der freien Schenkel C nennen.	Den Schnittpunkt A nennen.
5.	A und C sowie B und C verbinden.	B und C verbinden.		A und C verbinden.

Kreuze richtig an!

Die folgenden Aufgaben können auch mehrere richtige Antworten enthalten!

Welcher Begriff erklärt am besten "kongruenz"? (!flächengleich) (!seitengleich) (deckungsgleich)

Zwei Dreiecke, die aus einer Verschiebung entstanden sind, sind kongruent? (wahr) (!falsch)

Zwei Dreiecke, die aus einer Punktspiegelung entstanden sind, sind kongruent? (wahr) (!falsch)

Zwei Dreiecke sind kongruent, wenn sie in den Seitenlängen übereinstimmen? (wahr) (!falsch)

Zwei Dreiecke sind kongruent, wenn sie im Umfang übereinstimmen? (!wahr) (falsch)

Um zwei kongruente Dreiecke zu zeichenen braucht man... (!immer alle drei Winkel) (!mindestens zwei Seiten) (mindestens eine Seite) (!alle drei Winkel) (nicht zwingend einen Winkel) (mehr als zwei Angaben)

Zwei Dreiecke sind kongruent, wenn sie den gleichen Flächeninhalt haben? (!wahr) (falsch)

Zwei Dreiecke sind kongruent, wenn sie in allen drei Winkelgrößen übereinstimmen? (!wahr) (falsch)

Welche Angaben sichern die eindeutige Konstruierbarkeit eines Dreiecks!

(gleichseitig) (!rechtwinklig) (!gleichschenklig) (gleichschenklig-rechtwinklig)

Aus welchen Angaben kann man ein Dreieck eindeutig konstruieren?

(a=5cm b=6cm c=7cm) (!a=7cm $\beta$=112° $\gamma$=80°) (!a=3cm b= 5cm c= 9cm)

Sind die zwei Dreiecke kongruent?

(a=6,5cm c=5cm $\beta$=36° und a1=5cm, b1=6,5cm $\gamma$1=36°) (!a=7cm c=6cm $\alpha$=126 und a1=6cm, b1=7cm $\gamma$1=126°)

Gibt es den Kongruenzsatz SWW?

(!Ja, eine Seite und zwei Winkel sind ausreichende Angaben!) (Nein, aus diesem Satz lässt sich kein eindeutiges Dreieck konstruieren!)

Forscher oder Sternensammler

  leichte Aufgaben   leichte Aufgaben Lösungen

  normale Aufgaben   normale Aufgaben Lösungen

  schwierigere Aufgaben   schwierigere Aufgaben Lösungen

<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Kongruenz von Dreiecken,Mathematik,Kongruenz,Dreiecke,Dreieck,9. Klasse,Lernpfad</metakeywords>