Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Ziegen: Unterschied zwischen den Versionen
Main>Florian Bogner K (→Das „Ziegenproblem“: typo) |
Main>Florian Bogner K (→Das „Ziegenproblem“: typo) |
||
| Zeile 17: | Zeile 17: | ||
:Dann öffne folgende Seite mit einer anschaulichen Beschreibung in einem neuen Fenster. Betrachte aber noch nicht die Lösung! | :Dann öffne folgende Seite mit einer anschaulichen Beschreibung in einem neuen Fenster. Betrachte aber noch nicht die Lösung! | ||
{{Rechtsklick Fenster}} [http://www.mister-mueller.de/mathe/beispiele/ziege/ziegenproblem.html Ziegenproblem anschaulich erklärt] | |||
| Zeile 29: | Zeile 29: | ||
:Versuche dich an zwei Strategien: Behalte deine ausgewählte Tür oder wechsle die Tür jedes mal. | :Versuche dich an zwei Strategien: Behalte deine ausgewählte Tür oder wechsle die Tür jedes mal. | ||
{{Rechtsklick Fenster}}[http://www.shodor.org/interactivate/activities/AdvancedMontyHall/?version=1.6.0_13&browser=MSIE&vendor=Sun_Microsystems_Inc.&flash=10.0.22 Ziegenproblem, nur mit Schweinchen] | |||
| Zeile 123: | Zeile 123: | ||
:Würdest du '''jetzt''' wecheln??? | :Würdest du '''jetzt''' wecheln??? | ||
{{Rechtsklick Fenster}} [http://www.shodor.org/interactivate/activities/AdvancedMontyHall/?version=1.6.0_13&browser=MSIE&vendor=Sun_Microsystems_Inc.&flash=10.0.22 Ziegenproblem, nur mit Schweinchen] | |||
| Zeile 134: | Zeile 134: | ||
*Unter dem Wikipedia-Link kannst du dich noch genauer über die Hintergründe des Ziegenproblems informieren: | *Unter dem Wikipedia-Link kannst du dich noch genauer über die Hintergründe des Ziegenproblems informieren: | ||
{{Rechtsklick Fenster}}{{wpde|Ziegenproblem|Das Ziegenproblem}} | {{Rechtsklick Fenster}} {{wpde|Ziegenproblem|Das Ziegenproblem}} | ||
Version vom 29. September 2009, 06:38 Uhr
Das „Ziegenproblem“
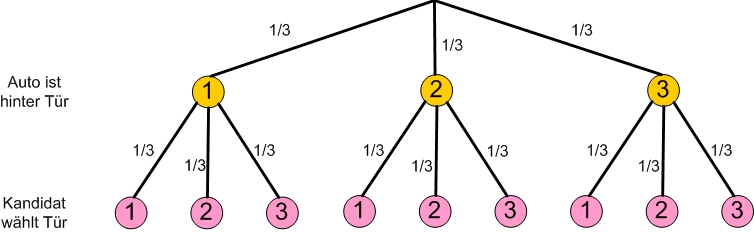
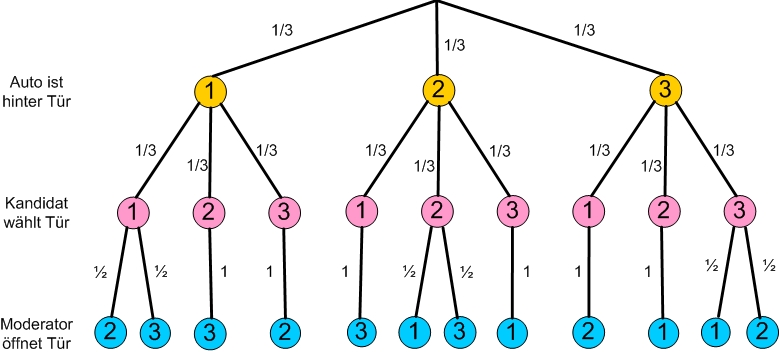
Ist es vorteilhaft für den Kandidaten zu wechseln? Löse die Aufgabe mit einem Baumdiagramm!
- Oder hast du das „Ziegenproblem“ noch nicht so richtig verstanden?
- Dann öffne folgende Seite mit einer anschaulichen Beschreibung in einem neuen Fenster. Betrachte aber noch nicht die Lösung!
Vorlage:Rechtsklick Fenster Ziegenproblem anschaulich erklärt
- Hast du dir schon überlegt, ob sich die Wahrscheinlichkeit beim Wechseln ändert und möchtest deine Hypothese überprüfen?
- Oder möchtest du einfach die Quiz-Show nachspielen?
- Dann öffne das Java-Applet und spiele das „Ziegenproblem“ nach! Die Türen öffnen sich durch anklicken. „Reset Doors“ schließt die Türen wieder.
- Versuche dich an zwei Strategien: Behalte deine ausgewählte Tür oder wechsle die Tür jedes mal.
Vorlage:Rechtsklick FensterZiegenproblem, nur mit Schweinchen
→ Versuche dich nun selbst an der Lösung des „Ziegenproblems“!
Brauchst du ein wenig Unterstützung, so bearbeite die folgenden Aufgaben Schritt für Schritt.
Lösungshilfe: Vorlage:Versteckt
Lösungshinweis: Vorlage:Versteckt
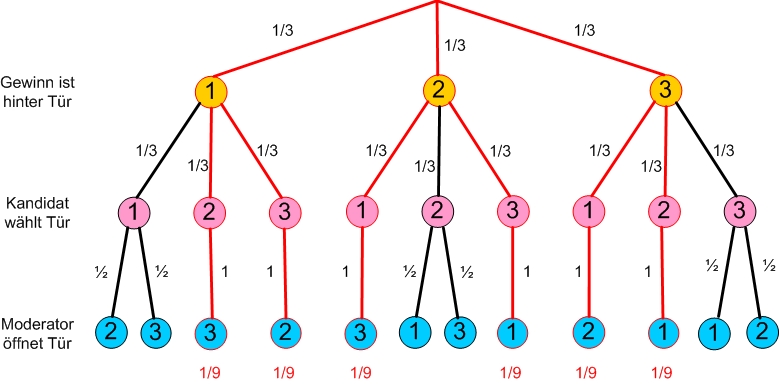
- Addiere die Wahrscheinlichkeiten der Pfade, bei denen der Kandidat gewinnt, wenn er prinzipiell die Tür wechselt. So erhälst du die Gewinnwahrscheinlichkeit „mit Wechsel“:
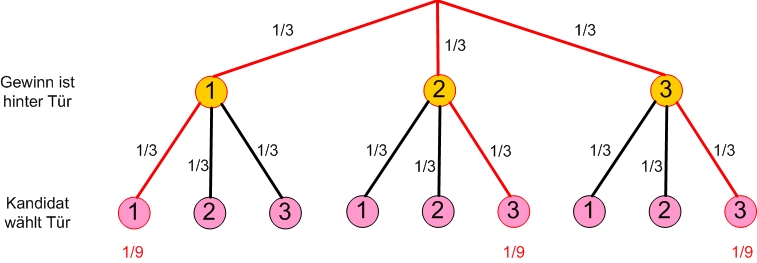
- Betrachten wir nun noch die Gegenwahrscheinlichkeit: die Gewinnwahrscheinlichkeit „ohne Wechsel“. Der Kandidat gewinnt in diesem Fall nur, wenn er sofort die richtige Tür wählt:
- Fazit: Wenn man die Türe wechselt verdoppelt sich die Gewinnwahrscheinlichkeit von auf !!!
Für Interessierte:
Interessiert dich das Ziegenproblem genauer, oder leuchtet dir die Lösung noch nicht ein?
- Öffne noch einmal das Ziegenproblem mit den Schweinchen. Du kannst die Anzahl der Türen erhöhen: Schiebe den Regler „Number of doors“ weiter nach rechts. Hast du eine Tür gewählt, öffnet der Moderator alle anderen Türen, bis auf die mit dem Hauptgewinn.
- Würdest du jetzt wecheln???
Vorlage:Rechtsklick Fenster Ziegenproblem, nur mit Schweinchen
- Du kannst jetzt auch unter dieser Seite die Erklärungen lesen.
Vorlage:Rechtsklick Fenster Ziegenproblem anschaulich erklärt
- Unter dem Wikipedia-Link kannst du dich noch genauer über die Hintergründe des Ziegenproblems informieren:
Vorlage:Rechtsklick Fenster Das Ziegenproblem![]()
Du hast den Lernpfad nun erfolgreich bewältigt. Vielen Dank fürs Mitmachen!