Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Efron: Unterschied zwischen den Versionen
Main>Florian Bogner (Lsg 4.2) |
Main>Florian Bogner (Lsg 4.4) |
||
| Zeile 69: | Zeile 69: | ||
{{Aufgaben-M|4.4|Bestimme die Gewinnwahrscheinlichkeiten aller verschiedenen Möglichkeiten. Übertrage die Tabelle in dein Heft und trage die Werte ein. Gibt es einen besten Würfel?}} | |||
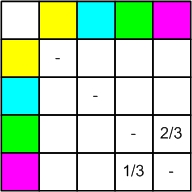
[[Datei:EfronTabelleLeer.jpg]] | |||
Tabelleneinträge: Wahrscheinlichkeit, dass Zeile gegen Spalte gewinnt. | |||
{{ | Lösungshilfe: {{versteckt|Hier ist noch einmal ein Beispiel. | ||
[[Datei:Efrongelbundblau.jpg|rechts|150px]] | |||
Wählt nun Pia zuerst den blauen Würfel, sucht sich danach Anna den gelben aus. | |||
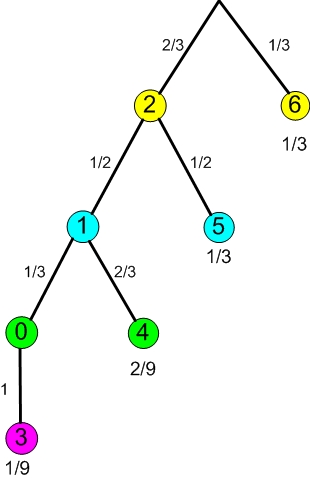
Das zugehörige Baumdiagramm sieht so aus: | |||
[[Datei:BaumEfrongelbundblau.jpg]] | |||
Noch einmal eine 36-Felder-Tafel: | |||
[[Datei:TafelEfrongelbundblau.jpg]] | |||
Der gelbe Würfel gewinnt mit einer Wahrscheinlichkeit von <math> \frac {24}{36} = \frac{2}{3}</math> gegen den blauen Würfel. | |||
}} | |||
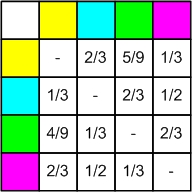
{{Lösung versteckt|[[Datei:EfronGewinntabelle.jpg]] | |||
Nein, es gibt keinen besten Würfel. Man findet zu jedem Würfel einen besseren, mit dem man mit einer Wahrscheinlichkeit von <math>\frac{2}{3}</math> gewinnt. | |||
Die beste Strategie zu gewinnen ist also '''höflich''' zu sein! | |||
}} | |||
'''Für Interessierte:''' | '''Für Interessierte:''' | ||
{{Aufgaben-M|4.5|Hans und Franz wollen bei Pia und Anna mitspielen. Wie groß ist die Wahrscheinlichkeit für jeden der Würfel, dass er gewinnt, wenn alle vier Würfel | {{Aufgaben-M|4.5|Hans und Franz wollen bei Pia und Anna mitspielen. Wie groß ist die Wahrscheinlichkeit für jeden der Würfel, dass er gewinnt, wenn alle vier Würfel geworfen werden?}} | ||
Lösungshilfe: {{versteckt|Jetzt musst du ein Baumdiagramm mit vier Stufen, die für die vier Würfel stehen, entwerfen. Zeichne so wenige Zweige wie möglich, damit es übersichtlich bleibt.}} | Lösungshilfe: {{versteckt|Jetzt musst du ein Baumdiagramm mit vier Stufen, die für die vier Würfel stehen, entwerfen. Zeichne so wenige Zweige wie möglich, damit es übersichtlich bleibt.}} | ||
| Zeile 100: | Zeile 124: | ||
Du hast übrigens die Pfadregeln kennengelernt. | |||
---- | ---- | ||
Version vom 3. September 2009, 21:07 Uhr
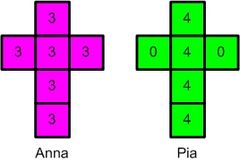
Die „Würfel von Efron“
Um dies herauszufinden, bastle dir die „Würfel von Efron“ ganz einfach nach. Nimm dazu beispielsweise vier helle Spielwürfel und beschrifte diese mit einem Folienstift so wie oben dargestellt, oder beklebe deine Würfel mit Papier. Jetzt spiele mit einem Freund oder einer Freundin nach den Spielregeln.
Lösungshinweise: Vorlage:Versteckt
Lösungshinweise: Vorlage:Versteckt
- Da Anna sicher eine 3 würfelt, gewinnt sie nur wenn Pia eine 0 würfelt.
- Nach Aufgabe 4.1 ist diese Wahrscheinlichkeit
- Das Ereignis „Pia gewinnt“ ist das Gegenereignis dazu und berechnet sich demnach folgendermaßen:
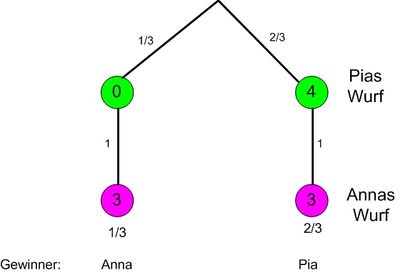
- Dies lässt sich auch aus dem folgenden Baumdiagramm erkennen:
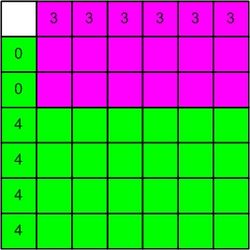
- Betrachte noch folgende 36-Felder-Tafel:
- Zählt man die Felder einfach ab, so folgt:
- Der grüne Würfel gewinnt mit einer Wahrscheinlichkeit von
- gegen den roten Würfel.
- Das stimmt mit unserem Baumdiagramm und der Rechnung überein!
Tabelleneinträge: Wahrscheinlichkeit, dass Zeile gegen Spalte gewinnt.
Lösungshilfe: Vorlage:Versteckt
Nein, es gibt keinen besten Würfel. Man findet zu jedem Würfel einen besseren, mit dem man mit einer Wahrscheinlichkeit von gewinnt.
Die beste Strategie zu gewinnen ist also höflich zu sein!
Für Interessierte:
Vorlage:Aufgaben-M
Lösungshilfe: Vorlage:Versteckt
Der gelbe Würfel gewinnt auf jeden Fall, falls er die 6 zeigt.
Dann sind die anderen Würfel uninteressant.
Falls er die 2 zeigt, muss der nächstbeste Würfel gesucht werden.
Als nächstes kann der blaue Würfel gewinnen, falls er 5 zeigt.
Wenn nicht, könnte der grüne Würfel gewinnen, falls er die 4 zeigt.
Hat bis jetzt keiner gewonnen, gewinnt der rote Würfel.
Du hast übrigens die Pfadregeln kennengelernt.