Flächeninhalt des Rechtecks

Flächeninhalt des Rechtecks

1. Arbeitsauftrag - Quiz über Rechtecke

Nun wollen wir zu Beginn erst einmal testen, was ihr denn noch über Vierecke wisst. Dazu könnt ihr jetzt ein Quiz machen. Quiz zum Viereck

2. Arbeitsauftrag - Kästchen zählen

Vorlage:Hinweis Zeit Ihr kennt bereits die verschiedenen geometrischen Figuren. Heute wollen wir uns mit dem Flächeninhalt von geometrischen Figuren beschäftigen.

Betrachtet dazu die Zeichnungen und ermittelt, aus wie vielen Kästchen die Rechtecke bestehen.

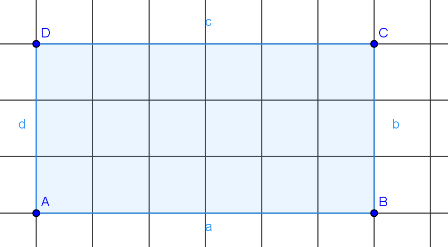
1. Rechteck

Hast du richtig gezählt?

Das Rechteck besteht aus ...

	16 Kästchen.
	18 Kästchen.
	20 Kästchen.

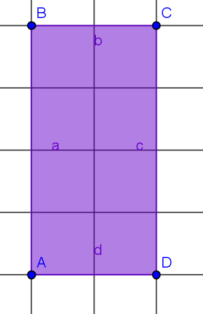
2. Rechteck

Hast du richtig gezählt?

Das Rechteck besteht aus ...

	8 Kästchen.
	6 Kästchen.
	7 Kästchen.

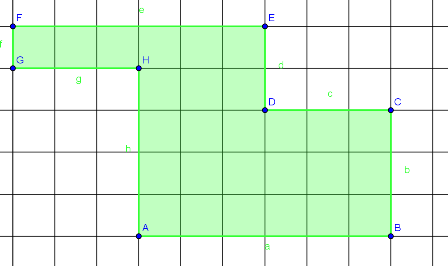
3. Rechteck

Hast du richtig gezählt?

Das Rechteck besteht aus ...

	8 1/2 Kästchen.
	9 Kästchen.
	8 Kästchen.

3. Arbeitsauftrag - Zeichnen

Vorlage:Hinweis Zeit Fertigt nun folgende Aufgabe in euerem Heft an: Zeichnet ein Rechteck mit Flächeninhalt 16 Kästchen.

Flächeninhalt eines Rechtecks

Ihr seht im nächsten Bild 3 verschiedene Rechtecke abgebildet:

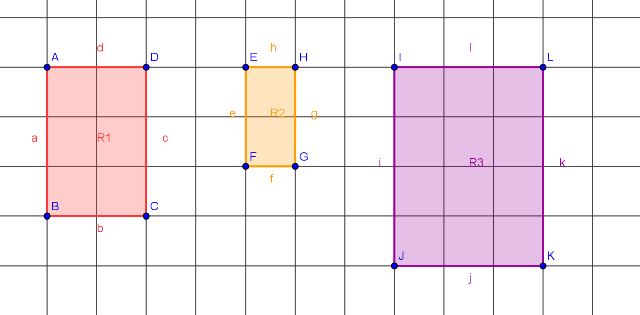
Wie ihr leicht sehen könnt, besteht das Rechteck R1 aus 6 Kästchen. Gleichzeitig sind die Seitenlängen des Rechtecks a = c = 3cm und b = d = 2cm.

Das Rechteck R2 besteht aus 2 Kästchen. Wie sind denn hier die Seitenlängen?

Das Rechteck R3 besteht aus 12 Kästchen. Könnt ihr auch hier die Seitenlängen angeben?

Was fällt euch dabei auf?

4. Arbeitsauftrag

Hefteintrag

Übertragt die Rechtecke in euer Heft. Schreibt dabei unter jedes Rechteck die Seitenlängen und den Flächeninhalt.

Aus unseren Beobachtungen sehen wir, dass die Anzahl der Kästchen eines Rechtecks

immer gleich des Produkts der beiden Seitenlängen ist.

Wir notieren:

Im Rechteck R1 haben wir die Seitenlängen a = 2 und b = 3 und der Flächeninhalt beträgt 2 x 3 = 6

Im Rechteck R2 haben wir die Seitenlängen e = 2 und f = 1 und der Flächeninhalt beträgt 2 x 1 = 2

Im Rechteck R3 haben wir die Seitenlängen i = 4 und j = 3 und der Flächeninhalt beträgt 4 x 3 = 12

Daher übertragen wir noch folgenden Satz in unserer Heft

Satz:

Flächeninhalt des Rechtecks

1. Die Fläche eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen.
2. Es gilt also: $F = a x b$

Ein anschauliches Beispiel

Zum Schluss könnt ihr nun noch beobachten, wie sich der Flächeninhalt eines Rechtecks ändert, wenn man die Seitenlängen verändert. Wenn ihr die Punkte der Schieberegler e und f nach links und rechts bewegt, ändert sich auch der Flächeninhalt des Rechtecks.

Weitere Aufgaben zum Flächeninhalt des Rechtecks

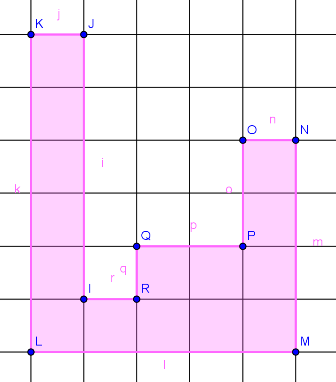
Andere geometrische Figuren

Wie könnte man den Flächeninhalt von diesen Figuren berechnen ohne die Kästchen zu zählen?

Bisher haben wir uns nur mit der Angabe des Flächeninhalt durch Kästchen beschäftigt. Nun wollen wir uns mit den Maßeinhalten bei Flächenberechnung beschäftigen.

Einheit	kurz	Umrechnung	Grafische Darstellung
Millimeter	mm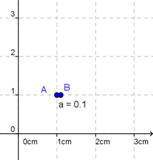
Zentimeter	cm	1 cm = 10 mm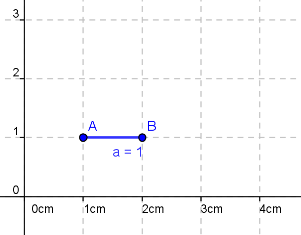
Dezimter: dm	dm	1 dm = 10 cm = 100 mm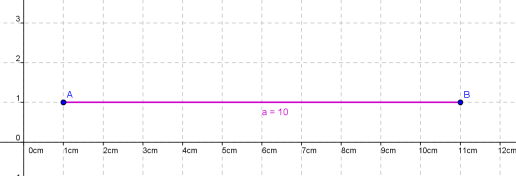
Meter	m	1 m = 10 dm = 100 cm = 1000 mm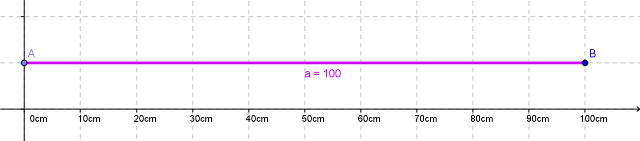
Kilometer	km	1 km = 1000 m = 10000 dm = 100000 cm = 1000000 mm	Datei:Kilometer.jpg

Check dein Wissen

1 Wie verändern sich der Flächeninhalt eines Rechtecks, wenn man eine Seitenlänge verdoppelt?

	Der Flächeninhalt bleibt gleich.
	Der Flächeninhalt verdoppelt sich
	Das Rechteck ist dann viermal so groß.

2 Der Umfang eines Rechtecks bleibt gleich wenn man eine beliebige Seitenlängen a verdoppelt und die andere Seitenlänge halbiert

	wahr
	falsch

3 Der Flächeninhalt eines Rechtecks bleibt gleich wenn man eine beliebige Seitenlängen a verdoppelt und die andere Seitenlänge halbiert

	wahr
	falsch

4 Die Werte von Flächeninhalt und Umfang sind beim Quadrat gleich groß

	wahr
	falsch

5 Der Umfang eines Rechtecks bleibt gleich, wenn man eine Seite um 2cm verkleinert, die andere Seite dafür aber um 2 cm verlängert. (Wichtig: Wir betrachten hier nur Rechtecke, bei denen beide Seiten mindestens 3 cm lang sind!!!)

	wahr
	falsch

6 Der Flächeninhalt eines Rechtecks bleibt gleich, wenn man eine Seite um 2cm verkleinert, die andere Seite dafür aber um 2 cm verlängert. (Wichtig: Wir betrachten hier nur Rechtecke, bei denen beide Seiten mindestens 3 cm lang sind!!!)

	wahr
	falsch

7 Die folgenden vier Fragen beziehen sich auf folgenden Sachverhalt: Ein Rechteck ist 4m lang und 9m breit. Welche Aussagen sind richtig?

Der Flächeninhalt beträgt 32m²

	wahr
	falsch

8 Der Umfang beträgt 26 cm²

	wahr
	falsch

9 Man kann 18 kleinere Rechtecke mit Flächeninhalt 2m² einbauen.

	wahr
	falsch

10 Ein Quadrat mit Seitenlänge 6m hat den gleichen Umfang.

	wahr
	falsch

Anwendungsaufgabe: Kinderzimmer

Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen.

Paul misst die beiden Kinderzimmer aus: Das erste ist 5 m lang und 4 m breit, das zweite 6 m lang und 3 m breit.

Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9."

Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an.

Für die ganz Schnellen bzw. für zu Hause

Klickt auf den folgenden Link und bearbeitet die Aufgaben zum Flächeninhalt. Vorlage:Hinweis Hausaufgabe1

Vorlage:Mitgewirkt