Lineare Funktionen/Station 2: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 72: | Zeile 72: | ||
{{3Spalten| | {{3Spalten| | ||
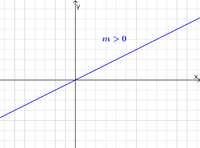
<math>m>0 </math> Gerade steigt nach rechts an | <math>m>0 </math> Gerade steigt nach rechts an | ||
[[Datei:Steigung positiv.png|200px|Steigung positiv]] | [[Datei:Steigung positiv.png|200px|Steigung positiv]] | ||
| | | | ||
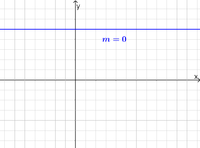
<math>m=0 </math> Gerade parallel zur x-Achse | <math>m=0 </math> Gerade parallel zur x-Achse | ||
[[Datei:Steigung Null.png|200px|Steigung Null]] | [[Datei:Steigung Null.png|200px|Steigung Null]] | ||
| | | | ||
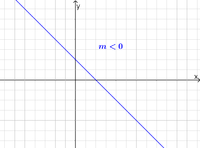
<math>m<0</math> Gerade fällt nach rechts ab | <math>m<0</math> Gerade fällt nach rechts ab | ||
[[Datei:Steigung negativ.png|200px|Steigung negativ]] | [[Datei:Steigung negativ.png|200px|Steigung negativ]] | ||
}} | }} | ||
Version vom 13. Juni 2018, 19:19 Uhr
Steigung einer Geraden
In Station 1 hast du dir noch einmal bewusst gemacht, dass Geraden im Koordinatensystem unterschiedlich steil verlaufen können.
Wie steil eine Gerade verläuft, gibt die sogenannte Steigung der Geraden an.
Wie du ebenfalls in Station 1 gesehen hast, enthält die Steigung einer Geraden wichtige Informationen darüber, wie schnell bzw. wie stark sich Größen in einer betrachteten Situation ändern.
In dieser Station lernst du, wie man die Steigung einer Geraden bestimmen und Geraden mit einer gewünschten Steigung zeichnen kann.
2.1 Für's Gefühl
Folgende App soll dir helfen, zunächst ein Gefühl dafür zu entwickeln, wie der Wert der Steigung mit der Lage der Geraden zusammenhängt.
Bewege den Schieberegler um die Steigung der Geraden zu verändern. Beobachte genau, wie zu einem Wert der Steigung die Gerade im Koordinatensystem verläuft! Wenn du fertig bist, scrolle nach unten, dann geht es weiter im Lernpfad.
Überprüfe, ob du die richtigen Erkenntnisse gezogen hast!
2.2 Wie bestimmt man die Steigung einer Geraden?
Nachdem du nun erfahren hast, wie der Wert der Steigung und die Lage einer Geraden im Koordinatensystem zusammenhängen, stellt sich jetzt die Frage, wie man denn den Wert der Steigung bestimmen kann!
Dein Cousin zeigt dir auf seinem Smartphone das unten dargestellte Foto. Er behauptet: "Diesen Berg bin ich gestern mit meinem Mountainbike hochgefahren!"
Was sagst du dazu? Wie stehst du zur Aussage deines Cousins?Mein Cousin ... (!...ist ein großer Lügner!) (...fährt oft Mountainbike, schon möglich, dass er so einen Berg raufgekommen ist.) (!... wäre höchstens da raufgekommen, wenn er geklettert wäre!)
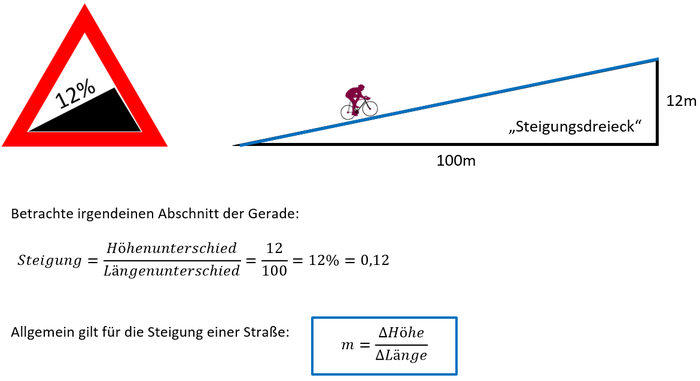
Um das Verkehrsschild zu verstehen, ist es wichtig zu wissen, wie denn eine Steigung überhaupt festgelegt ist.
Betrachte die "versteckte" Grafik. Erkläre in einem Satz, was eine Steigung von 100% ausdrückt und notiere diesen Satz in dein Schulheft.
Die Steigung von Geraden bestimmt man allgemein genauso wie die Steigung von Straßen, nämlich mithilfe von Steigungsdreiecken.
Um das genauer zu erforschen, bearbeite bitte folgende App:
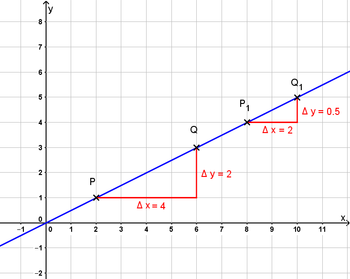
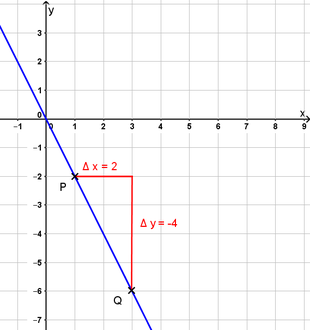
- Bewege die Punkte P und Q auf der Geraden. Beobachte, wie sich der Quotient zur Berechnung der Steigung dabei verändert.
- Verändere mit dem Schieberegler die Steigung der Geraden und versuche das Steigungsdreieck so einzustellen, dass die Koordinaten der Punkte P und Q gut abzulesen sind.
Prüfe dich!
Welche Antworten sind richtig? (!Die Steigung hängt davon ab, wo die Punkte P und Q auf der Geraden liegen.) (Je größer bei gleichem ist, desto größer ist die Steigung.) (Zur Berechnung der Steigung ist es vollkommen egal, wo auf der Gerade das Steigungsdreieck liegt.) (Das Steigungsdreieck ist immer rechtwinklig!)
Die Steigung einer Geraden bestimmt man mithilfe eines Steigungsdreiecks.
- Wähle zwei beliebige Punkte P und Q auf der Geraden aus, am besten so, dass man die Koordinaten gut ablesen kann.
- Lege das Steigungsdreieck in diesen Punkten an die Gerade an.
- Berechne die Steigung m:
Unterscheide drei Fälle:
Gerade steigt nach rechts an
Gerade parallel zur x-Achse
Gerade fällt nach rechts ab
| Beispiel 1 | Beispiel 2 | |
 |
 | |
| oder | ||
Schätze doch mal ab, wie groß die Steigung war, die dieser Audi Quattro vor 30 Jahren bereits erkommen hat!
Übung 4: Wie groß ist die Steigung?
Führe die Übung in der App durch. Notiere deine Überlegungen und Berechnungen ins Übungsheft!!In der App musst du Dezimalzahlen nicht mit Komma, sondern mit Punkt eintragen! Wenn es dir hilft, kannst du die Darstellungen auch in dein Heft übernehmen, um dort das Steigungsdreieck einzuzeichnen.
|
Probleme zu verstehen, wie man die Steigung bestimmt? Dann kannst du hier hier die Steigungsbestimmung nochmal Schritt für Schritt nachzuvollziehen! Keine Probleme? Dann kannst du einfach weitermachen! :)] |
2.3 Zeichnen einer Geraden unter Ausnutzung der Steigung
In diesem Kapitel beschäftigen wir uns mit der umgehehrten Fragestellung:
Überlege: Wie kannst du deine Kenntnisse nutzen, um eine Ursprungsgerade mit vorgegebener Steigung zu zeichnen, ohne dass du erste eine Wertetabelle anlegen musst?
Beispiel: Zeichne eine Ursprungsgerade mit der Steigung !
Gehe ganz grob umgekehrt vor wie oben:
- Du musst zunächst einen Punkt kennen, der auf der Geraden liegt (Tipp: Ursprungsgerade!)
- Da die Steigung gegeben ist, kennst du und .
- Damit kannst du vom gegebenen Punkt aus das Steigungsdreieck zeichnen und erhältst so einen zweiten Punkt.
- Da eine Gerade durch zwei Punkte festgelegt ist, musst du jetzt nur noch die beiden Punkte verbinden.
Du hast die Idee nicht verstanden? Kein Problem, in diesem Fall kannst du es dir hier nochmal ausführlich erklären lassen!
5.
- Zeichne in deinem Schulheft eine Ursprungsgerade mit der Steigung in ein Koordinatensystem ein.
- Schreibe in deinen eigenen Worten stichpunktartig auf, wie du allgemein vorgehen musst. Wenn du dir nicht sicher bist, kannst du dir die "Idee" oben anzeigen lassen.
Nicht sicher, ob deine Lösung stimmt? Hier ist ein ähnliches Beispiel ausführlich dargestellt!
Glückwunsch, du hast die zweite Station erfolgreich gemeistert! Es warten Aufgaben auf dich...! :)
