Lineare Funktionen/Station 1: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 97: | Zeile 97: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
{{Merke| | {{Box|1=Merke|2= | ||
Bei '''direkt proportionalen''' Zuordnungen <math>f: x \mapsto y </math> gilt <math>\frac{y}{x}=m</math> mit '''konstantem''' <math>m</math> ''(Proportionalitätskonstante).'' <br> | |||
Direkt proportionale Zuordnungen können also durch die Funktionsgleichung '''<math>\color{blue}y=m\cdot x</math>''' bzw. <math>\color{blue}f(x)=m\cdot x</math> beschrieben werden.<br>Man nennt sie deshalb auch <span style = "color:blue">proportionale Funktionen</span>. | Direkt proportionale Zuordnungen können also durch die Funktionsgleichung '''<math>\color{blue}y=m\cdot x</math>''' bzw. <math>\color{blue}f(x)=m\cdot x</math> beschrieben werden.<br>Man nennt sie deshalb auch <span style = "color:blue">proportionale Funktionen</span>. | ||
}} | |3=Merksatz}} | ||
{{Box|1=Aufgabe 1 Fortsetzung 1|2= | |||
'''d)''' | |||
*Nutze die Funktionsgleichung, um die Wassermenge zu den Zeitpunkten 0h, 3h, 1,5h und 8h zu berechnen. | |||
*Trage diese Punkte in ein Koordinatensystem ein, um den Graphen der Funktion zu zeichnen. | |||
*Ist es sinnvoll, die Punkte zu verbinden? Begründe! | |||
Verwende folgende '''Vorgaben:''' | Verwende folgende '''Vorgaben:''' | ||
| Zeile 113: | Zeile 116: | ||
:y-Achse: 1cm<math> \widehat{=}</math> 200m<sup>3</sup> | :y-Achse: 1cm<math> \widehat{=}</math> 200m<sup>3</sup> | ||
{{Lösung versteckt|1= | |||
mit <math>f(t)=m\cdot t</math> und m=120m<sup>3</sup>/h folgt: | mit <math>f(t)=m\cdot t</math> und m=120m<sup>3</sup>/h folgt: | ||
| Zeile 128: | Zeile 131: | ||
Ja, es macht Sinn, die Punkte zu verbinden, da zu jeder Zeit zwischen den gegebenen ebenfalls eine beistimmte Wassermege eingetreten ist. | Ja, es macht Sinn, die Punkte zu verbinden, da zu jeder Zeit zwischen den gegebenen ebenfalls eine beistimmte Wassermege eingetreten ist. | ||
}} | |||
|3=Arbeitsmethode}} | |||
Version vom 10. Juni 2018, 12:43 Uhr
Station 1: Proportionale Funktionen
Im Bergwerk
In tief gelegene Bergwerke dringt im Betrieb laufend Grundwasser ein. Daher benutzt man große Pumpen, um das Grundwasser wieder aus dem Berkwerk zu befördern und damit den Bergleuten ein Arbeiten im Trockenen zu ermöglichen.
In der Regel treten pro Stunde etwa 120m³ Grundwasser ein, die ständig abgepumpt werden müssen.
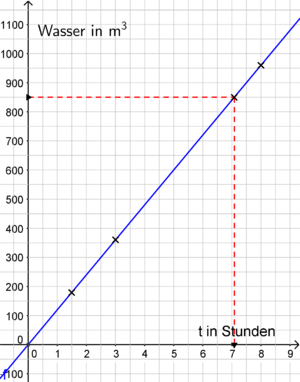
Plötzlich fallen die Pumpen aus! Die Kumpel werden sichtlich nervös, denn der Aufzug ist langsam und kann immer nur wenige Leute nach oben in Sicherheit bringen. Und jeder weiß, sobald 850m3 Wasser ins Bergwerk eindringen, fällt der Strom und damit der Aufzug aus. Doch ihr seid kühle Mathematiker und könnt herausfinden, wie lange für die Evakuierung noch Zeit bleibt.
Um auch sicherzugehen, dass ihr euch nicht verrechnet, wärmt ihr euch zunächst mit ein paar einfachern Aufgaben auf. Es geht ja schließlich um das Leben der Bergleute!
a) Wie viel Wasser dringt in einer halben Stunde in das Bergwerk ein? Begründe dein Ergebnis! Gib eine Zuordnungsvorschrift an, die die Situation beschreibt.
Aufgrund der direkten Proportionalität gilt:
1h 120m3
0,5h 60m3
Zuordnungsvorschrift: f: Zeit t (in h) --> Wassermenge w (in m3b) Berechne in einer Wertetabelle die eingedrungene Wassermenge nach 1,2,5 und 6 Stunden. Bestimme die Proportionalitätskonstante m.
Zeit in h
Heißt die Proportionalitätskonstante nicht c?
c) Nutze den Wert m, um die eingedrungene Wassermenge nach 4h, 5,5h und 1,63h zu berechnen.
Gib eine Funktionsgleichung bzw. einen Funktionsterm an,
wie man mit der Proportionalitätskonstante m die Wassermenge zu jeder Zeit t berechnen kann.
allgemeine Funktionsgleichung: oder
f(4h) = 120 m3 /h * 4h = 480 m3
f(5,5h) = 120 m3/h * 5,5h = 660m3
f(1,63h) = 120 m3/h * 1,63h = 195,6 m3Bei direkt proportionalen Zuordnungen gilt mit konstantem (Proportionalitätskonstante).
Man nennt sie deshalb auch proportionale Funktionen.
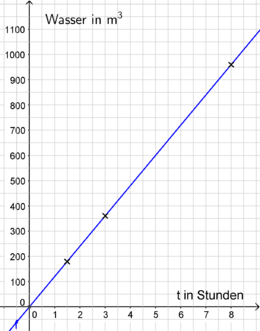
d)
- Nutze die Funktionsgleichung, um die Wassermenge zu den Zeitpunkten 0h, 3h, 1,5h und 8h zu berechnen.
- Trage diese Punkte in ein Koordinatensystem ein, um den Graphen der Funktion zu zeichnen.
- Ist es sinnvoll, die Punkte zu verbinden? Begründe!
Verwende folgende Vorgaben:
- x-Achse: 1cm 2h
- y-Achse: 1cm 200m3
Genug aufgewärmt, die Kumpel wollen endlich wissen, wie lange sie noch Zeit haben!!
<popup name="Lösung">
Nach ca. 7,1 Stunden muss spätestens der letzte Bergmann den Stollen verlassen haben, da dann der Aufzug ausfällt. </popup>
Ah, kein Stress,das ist ja noch genug Zeit. Bis du an der Reihe bist kannst du in aller Ruhe noch eine kleine Aufgabe lösen...
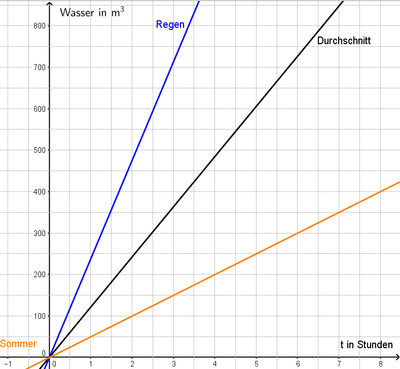
Nach einem regnerischen Herbstmonat dringen pro Stunde sogar 240m3 in das Bergwerk ein, in trockenen Sommermontaten hingegen nur 50m3.
- Gib für die beiden Fälle eine Funktionsgleichung an, die die Situation richtig beschreibt.
<popup name="Lösung">
- Herbst:
- Sommer:
</popup>
- Zeichne die Graphen zu den beiden Funktiongleichungen in dein Koordinatensystem aus Aufgabe 2.
<popup name="Tipp">
- Um die Graphen zu zeichnen musst du mithilfe der Funktionsgleichung zunächst Wertepaare berechnen (z.B. in einer Wertetabelle)
- Überlege: Wie viele Wertepaare/Punkte benötigst du, um den Graphen zeichnen zu können?
</popup>
- Beschreibe, was dir auffällt, wenn du die Graphen miteinander vergleichst.
- Erkläre in einem Satz, wie sich die Unterschiede erklären lassen!
<popup name="Lösung">
- Alle drei Graphen sind Ursprungsgeraden
- Die Geraden verlaufen unterschiedlich steil
Je größer die Zuflussmenge pro Zeit ist, also je größer die Proportionalitätskonstante ist, desto steiler verläuft die Gerade des zugehörigen Graphen.
</popup>
Allgemein:
Die Funktion mit der Funktionsgleichung beschreibt die direkte Proportionalität der beiden Variablen x und y.
Der Graph dieser Funktion ist eine Gerade durch den Ursprung des KS; dabei ist m die Steigung dieser Geraden.
Super, du hast die erste Station geschafft! Überprüfe in der Übungsstation doch gleich, ob du alles verstanden hast!