Kürzen von Brüchen

zurück zum Lernpfad Brüche erweitern

Das ist ja viel übersichtlicher, wenn man im Zähler und im Nenner nicht so große Zahlen stehen hat,
das findest du doch auch, oder?!

Station Los geht's, wir machen alles übersichtlicher!

Vorlage:Rechtsklick Fenster In diesem Zimmer liegt alles herum. Hilf mit, dann geht es schneller.

Nachdem du beim Zimmeraufräumen geholfen hast, kannst du dich mit deinen Freunden verabreden.
Vorlage:Rechtsklick Fenster Sortiere doch schon mal die Süßigkeiten, damit jeder das bekommt, was ihm schmeckt.

Du hast gesehen, dass du aus einem Bruch, wie   $\frac{6}{18}$   durch sortieren

oder aufräumen den Bruch   $\frac{1}{3}$   zaubern kannst.

Aber was steckt hier dahinter?

Dazu schau dir die folgende Aufgabe an.

Welcher Bruchteil ist zu Beginn blau gefärbt? Welcher Bruchteil ist gefärbt, wenn du das Kästchen drückst?

Damit die Zahlen im Zähler und im Nenner nicht so groß sind, kannst du einzelne Unterteilungen entfernen, aber nicht alle.

Willst du versuchen, ob du unnötige Unterteilungen entfernen kannst?

Vorlage:Rechtsklick Fenster Hier hast du die Möglichkeit, es herauszufinden.

Station Einführung Kürzen

Begriff Kürzen

Was du gerade gemacht und beobachtet hast, nennt sich Kürzen.

Beim Kürzen eines Bruches vergröberst du die gezeigten Bruchteile, indem du die unnötigen Unterteilungen entfernst.

Wie du gesehen hast, ändert sich auch beim Kürzen der Bruchteil nicht.

Kommt dir das bekannt vor?

Kürzen ist das Gegenteil von Erweitern, allerdings mit einigen Besonderheiten.

Die Rechnung, die dahinter steckt

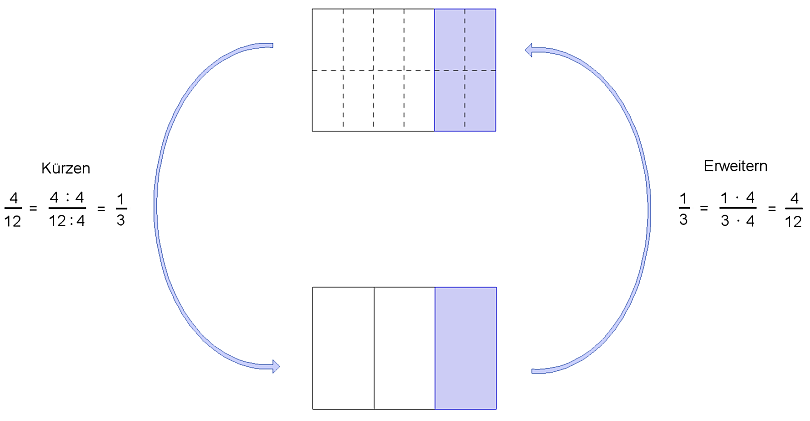
Hier hast du ein Rechteck. Von dem Rechteck sind   $\frac{12}{24}$   blau gefärbt.

Der Bruchteil lässt sich kürzen, dazu musst du den Schieberegler verschieben.

Bearbeite nun folgende Aufgaben und schreibe alles auf deinen Laufzettel, du wirst die Antworten noch brauchen.

Welche Zahlen sind zum Kürzen eingestellt? Kürze nun mit 2. Wie verändert sich der Zähler? Kürze als nächstes mit 6. Wie verändert sich der Nenner? Kürze zum Schluss mit 4. Wie verändern sich Zähler und Nenner? Überlege dir, warum es die 5 nicht auf dem Schieberegler gibt.

Quiz: Hast du alle Fragen richtig beantwortet?

Das waren ganz schön viele Fragen! Teste dich selbst, was und wieviel du richtig beantwortet hast.

Vorlage:Rechtsklick Fenster Hier geht's lang.

Station Kürzen

Schreibe dir den Merksatz in dein Heft:

  Ein Bruch wird gekürzt, indem man den Zähler und den Nenner durch die selbe Zahl dividiert.
  Diese Zahl ist ein gemeinsamer Teiler von Zähler und Nenner.
 
  Beispiel: $\frac{12}{18}=\frac{12 : 6}{18 : 6}=\frac{2}{3}$

Wie oft und mit welchen Zahlen kannst du einen Bruch kürzen?

Kreuze die Antwort an, von der du glaubst, sie sei richtig.

Wenn du alle Fragen beantwortet hast, klicke auf die Korrektur-Taste.

Dass die Zahl, mit der du kürzen kannst, ein gemeinsamer Teiler von Zähler und Nenner sein muss,

hast du schon festgestellt.

Wie viele gemeinsame Teiler von Zähler und Nenner findest du...

1   ...für den Bruch  $\frac{4}{8}$ ?

	zwei, nämlich 2 und 4
	einen, nämlich 4
	drei und zwar 1, 2 und 4

2   ...für den Bruch  $\frac{1}{8}$ ?

	zwei, nämlich 2 und 4
	einen, nämlich 1
	keinen

3 Die 1 ist immer ein gemeinsamer Teiler von Zähler und Nenner, denn jede Zahl ist durch 1 teilbar.
Was machst du, wenn du keinen gemeinsamen Teiler außer 1 findest?

	Ich kann zwar mit 1 kürzen, aber der Bruch ändert sich dadurch nicht.
	Das passiert nicht. Man findet immer noch weitere gemeinsame Teiler!

4 Kannst du mit 0 kürzen?

	Ja
	Nein

Das ist wichtig, bitte schreibe dir den folgenden Merksatz in dein Heft.

Vorlage:Versteckt

Wie kannst du einen Bruch vollständig kürzen?

Vorlage:Rechtsklick Fenster Finde es heraus!

Um einen Bruch vollständig zu kürzen, kürzt du solange mit gemeinsamen Teilern
von Zähler und Nenner, bis du keinen außer 1 mehr findest.

Die Zeit läuft ab jetzt...

In einer Stegreifaufgabe oder in einer Schulaufgabe ist die Zeit knapp!

Wenn du kürzen sollst, dann musst du dem Zähler und dem Nenner einen gemeinsamen Teiler ansehen.

Aber erinnerst du dich noch an die Teilbarkeitsregeln?

Sie können dir helfen einen gemeinsamen Teiler schneller zu sehen.

Jetzt solltest du fit sein und gemeinsame Teiler auch in kurzer Zeit finden können.

Station Übungen zum Kürzen

Bearbeite von links nach rechts alle vier Übungen.

Gibt es mehrere Aufgaben oder Schwierigkeiten zur Auswahl, dann musst du nur eine der Aufgaben bearbeiten.

Die Farben können dir bei deiner Entscheidung helfen:

leicht

mittelschwer

schwer

1. Übung		2. Übung		3. Übung		4. Übung
Kürze!		Mit welcher Zahl wurde gekürzt? oder Quiz: Findest du die passende Zahl?		Quiz: Richtig oder falsch gekürzt?		Kürze so weit wie möglich
Vorlage:Rechtsklick Fenster leicht		Vorlage:Rechtsklick Fenster Mit welcher Zahl wurde gekürzt?
Vorlage:Rechtsklick Fenster mittelschwer		Vorlage:Rechtsklick Fenster Quiz mittelschwer		Vorlage:Rechtsklick Fenster Findest du den Fehler?		Vorlage:Rechtsklick Fenster mittelschwer
		Vorlage:Rechtsklick Fenster Quiz schwer				Vorlage:Rechtsklick Fenster schwer

[[../Größenvergleich von Brüchen|weiter zum Lernpfad Brüche vergleichen]]