Einführung in quadratische Funktionen/Übungen 1: Unterschied zwischen den Versionen
Main>Martin Schendzielorz Keine Bearbeitungszusammenfassung |
Main>Martin Schendzielorz Keine Bearbeitungszusammenfassung |
||
| Zeile 142: | Zeile 142: | ||
'''Lösung zur Aufgabe 4:'''<br /> | '''Lösung zur Aufgabe 4:'''<br /> | ||
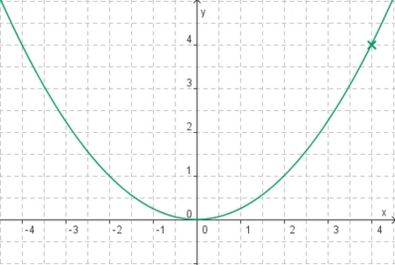
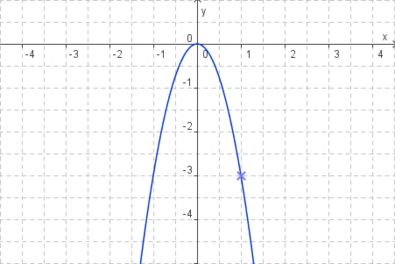
a) {{Lösung versteckt|1=:#Der Punkt (4/4) liegt auf der Parabel. Es gilt also 4 = a·4<sup>2</sup>. Damit ist a = 0,25. }} b) {{Lösung versteckt|1=:#Der Punkt (1/-3) liegt auf der Parabel. Es gilt also -3 = a·1<sup>2</sup> Damit ist a = - 3. }} | a) {{Lösung versteckt|1=:#Der Punkt (4/4) liegt auf der Parabel. Es gilt also 4 = a·4<sup>2</sup>. Damit ist a = 0,25. }} b) {{Lösung versteckt|1=:#Der Punkt (1/-3) liegt auf der Parabel. Es gilt also -3 = a·1<sup>2</sup> Damit ist a = - 3. }} | ||
== Schreibe dir nun die Aufgaben auf die du (und dein Partner evtl.) nicht lösen konntest bzw. deren Aufgabenstellung du nicht verstanden hast! Schreibe auf womit du dir schwer getan hast. == | |||
---- | ---- | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
Version vom 12. März 2010, 11:26 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3
| Die zulässige Höchstgeschwindigkeit beträgt innerhalb geschlossener Ortschaften 50 km/h. Unter idealen Bedingungen sollte ein Pkw in einer Gefahrensituation rechtzeitig vor Erreichen der Gefahrenstelle bremsen können. Der Wert der Bremsbeschleunigung aB und damit die Länge des Bremsweges ist aber u.a. abhängig von den Straßenverhältnissen. In der Tabelle sind einige Werte für die Bremsbeschleunigung eines Pkws auf einer asphaltierten Straße bei unterschiedlichen Witterungsverhältnissen angegeben.
Ordne dem gegebenen Bremsweg s die passende Bremsbeschleunigung aB und die Straßenverhältnisse zu. Tipp: Du kannst die Übung durch Rechnen, mit Hilfe eines GeoGebra-Applets oder durch Nachdenken lösen. |
|
| s = 13 m | aB = 7,4 m/s2 | trockener Asphalt |
| s = 18 m | aB = 5,4 m/s2 | nasser Asphalt |
| s = 80 m | aB = 1,2 m/s2 | Glatteis |
| s = 37 m | aB = 2,6 m/s2 | Neuschnee |
Aufgabe 2: Lückentext
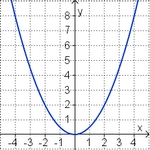
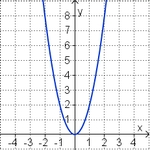
Die Graph der Funktion f mit f(x)=ax² heißt Parabel . Ist a = 1, so heißt der Graph Normalparabel.
Quadratische Funktionen mit dem Funktionsterm ax² liegen symmetrisch zur y-Achse.
Der Punkt S (0;0) heißt Scheitel .
Für a>0 gilt: Je größer a ist, desto steiler ist die Parabel.
Für a>0 gilt: Je kleiner a ist, desto weiter ist die Parabel.
Aufgabe 3: Zeichne die Graphen von folgenden Funktionen auf ein kariertes Blatt!
a) f(x)= x²
b) f(x)= 3x²
c) f(x)= -3x²
d) f(x)= 1/2 x²
e) f(x)= -1/2 x²
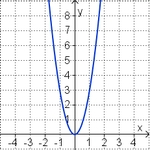
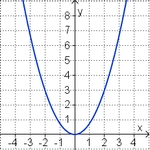
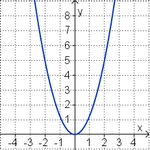
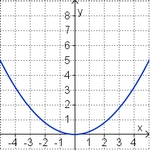
Aufgabe 5: Term und Graph zuordnen
Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 6: Multiple Choice
Kreuze die zutreffenden Aussagen an. Es sind jeweils mehrere Antworten richtig.
f(x) = 3,5x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|14] liegt auf dem Graphen.) (Der Punkt [14|2] liegt nicht auf dem Graphen.)
f(x) = - 0,5x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-2] liegt auf dem Graphen.) (!Der Punkt [2|2] liegt auf dem Graphen.)
f(x) = - 2x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.)
f(x) = 0,2x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.)
Lösung zur Aufgabe 3:
Lösung zur Aufgabe 4:
a)
- Der Punkt (4/4) liegt auf der Parabel. Es gilt also 4 = a·42. Damit ist a = 0,25.
b)
Schreibe dir nun die Aufgaben auf die du (und dein Partner evtl.) nicht lösen konntest bzw. deren Aufgabenstellung du nicht verstanden hast! Schreibe auf womit du dir schwer getan hast.

|
Als nächstes beschäftigst du dich mit dem Anhalteweg. |