Quadratische Funktionen erkunden/Quadratische Funktionen kennenlernen

Quadratische Funktionen erkunden

• Wiederholung
• Quadratische Funktionen im Alltag
• Quadratische Funktionen kennenlernen
• Die Parameter der Scheitelpunktform
• Die Scheitelpunktform
• Die Parameter der Normalform
• Die Normalform
• Von der Scheitelpunkt- zur Normalform
• Übungen

< Mathematik-digital

Quadratische Funktionen – was genau bedeutet das überhaupt?

Die Worte für sich kannst du schon einordnen. Ein Quadrat ist eine geometrische Figur bei der alle Seiten gleich lang sind. Was Funktionen sind, konntest du auf den letzten Seiten dieses Lernpfades ausführlich wiederholen.

Schauen wir uns doch einmal an, ob wir eine Verbindung zwischen Quadraten und Funktionen herstellen können, die uns schließlich zu Quadratischen Funktionen führt.

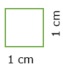
Dazu zeichnen wir ein Quadrat mit der Seitenlänge 1 cm und berechnen dessen Flächeninhalt:

A = 1 cm ⋅ 1 cm = 1² cm²= 1 cm²

Dasselbe können wir nun mit Quadraten der Seitenlängen 2 cm, 3 cm und 4 cm machen und die Werte in einer Tabelle zusammenfassen:

Seitenlänge	Fläche
1 cm	1 cm2
2 cm	4 cm2
3 cm	9 cm2
4 cm	16 cm2

Für ein beliebiges Quadrat kann man die Seitenlänge mit x bezeichnen. Mit der Formel für den Flächeninhalt des Quadrates ergibt sich dann A = x². Den Flächeninhalt kannst du als Funktion von x ansehen und f(x) = x² oder y = x² schreiben.

x	y = x2
1	1
2	4
3	9
4	16

Wie sieht der Graph dieser Funktion wohl aus?

Aufgabe 1

Für diese Aufgabe benötigst du dein Notizbuch .

a) Ergänze die Tabelle um weitere Werte, die dir helfen den passenden Graph in ein Koordinatensystem einzuzeichnen.

b) Zeichne den zugehörigen Graphen in ein Koordinatensystem.

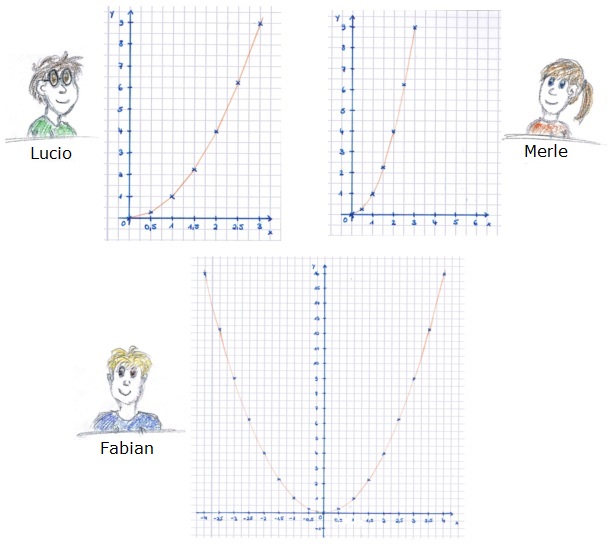
Lucio, Merle und Fabian haben unterschiedliche Lösungen zu dieser Aufgabe. Schaue dir ihre Lösungen an und vergleiche, ob eine davon deiner eigenen Lösung ähnelt. <popup name="Lösungen von Lucio, Merle und Fabian">

</popup>

Die drei diskutieren über ihre Lösungen und versuchen herauszufinden, wer von ihnen die richtige Lösung gefunden hat. Vielleicht haben ja auch mehrere recht?

Aufgabe 2

Für diese Aufgabe benötigst du dein Notizbuch .

Lies dir die Argumente von Lucio, Merle und Fabian durch und führe die Diskussion mit deinem Partner weiter. Beachtet dabei auch eure eigenen Lösungen von Aufgabe 1 und lasst sie in eure Diskussion mit einfließen. Wer hat die richtige Lösung gefunden?

Notiert eure Schlussfolgerungen in euren Notizbüchern. Dabei solltet ihr nicht nur die Lösung aufschreiben, sondern auch die Argumente, die euch dazu geführt haben.

Erstellt von Elena Jedtke