Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 40: | Zeile 40: | ||
{{Box|7. Zeichne die Gerade!| | {{Box|7. Zeichne die Gerade!| | ||
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks! | Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks! | ||
a) <math>f(x)=1,5\cdot x</math> | a) <math>f(x)=1,5\cdot x</math> | ||
b) <math>g(x)=-\frac{1}{4}\cdot x</math> | b) <math>g(x)=-\frac{1}{4}\cdot x</math> | ||
|Üben}} | |Üben}} | ||
Aktuelle Version vom 4. Januar 2025, 16:22 Uhr
5. Wie war das jetzt nochmal?
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
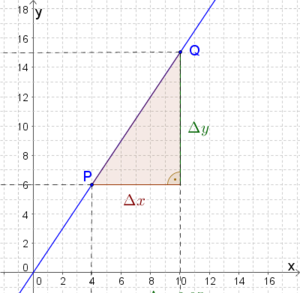
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
y x = (yQyP)(xQxP)(156)(104)1,5
Die Steigung der dargestellten Geraden ist 1,5
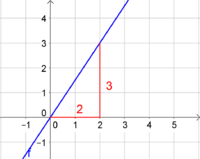
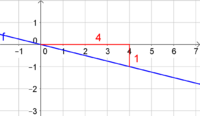
6. Wie groß ist die Steigung?
Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.
- Notiere dein Rechnungen und Überlegungen im Übungsheft.
- Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
Die lilafarbene Gerade gehört zu einer proportionalen Funktion, da sie durch den Ursprung verläuft.
Ihre Steigung ist .
Zur Berechnung der Steigung kann man z.B. die Punkte und verwenden.
7. Zeichne die Gerade!
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
a)
b)
Wandle zunächst die Steigung 1,5 in einen Bruch um!
a) 
Alles geschafft? Super, dann auf zu Station 3!
