Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 23: | Zeile 23: | ||
{{Box|6. Wie groß ist die Steigung?| | {{Box|6. Wie groß ist die Steigung?| | ||
[[Datei:Lernpfad lineare Funktionen Station 2 Übung 6.png|right| | [[Datei:Lernpfad lineare Funktionen Station 2 Übung 6.png|right|500px|Graphen linearer Funktionen]] | ||
Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung. | Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung. | ||
Version vom 4. Januar 2025, 16:21 Uhr
5. Wie war das jetzt nochmal?
Fülle den Lückentext aus, um die Steigung der Geraden zu berechnen.
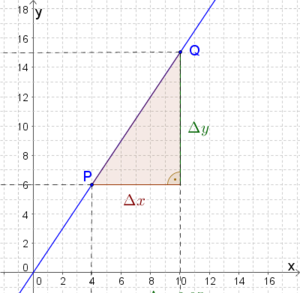
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
y x = (yQyP)(xQxP)(156)(104)1,5
Die Steigung der dargestellten Geraden ist 1,5
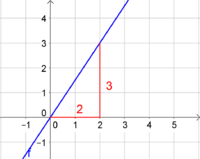
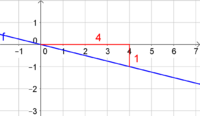
6. Wie groß ist die Steigung?
Die lilafarbene Gerade gehört zu einer proportionalen Funktion, da sie durch den Ursprung verläuft.
Ihre Steigung ist .
Zur Berechnung der Steigung kann man z.B. die Punkte und verwenden.
7. Zeichne die Gerade!
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
- a)
- b)
Wandle zunächst die Steigung 1,5 in einen Bruch um!
Alles geschafft? Super, dann auf zu Station 3!