Lineare Funktionen/Station 2/Übung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 30: | Zeile 30: | ||
|Üben}} | |Üben}} | ||
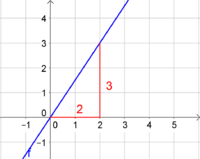
{{Lösung versteckt|1=<span style="color:blue">Die lilafarbene Gerade gehört zu einer proportionalen Funktion. Ihre Steiung ist <math>m=\frac{1}{3}</math> </span> | {{Lösung versteckt|1=<span style="color:blue">Die lilafarbene Gerade gehört zu einer proportionalen Funktion. Ihre Steiung ist <math>m=\frac{1}{3}</math> </span>. Zur Berechnung der Steigung kann man z.B. die Punkte O(0|0) und A(3|1) verwenden. }} | ||
Version vom 4. Januar 2025, 15:15 Uhr
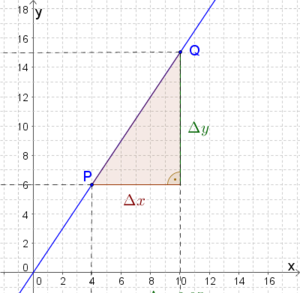
Die Steigung m berechnet man mithilfe des Steigungsdreiecks.
y x = (yQyP)(xQxP)(156)(104)1,5
Die Steigung der dargestellten Geraden ist 1,5
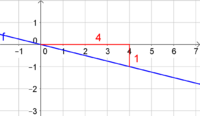
Finde in der Abbildung diejenige Gerade, die zu einer proportionalen Funktion passt, und berechne deren Steigung.
- Notiere dein Rechnungen und Überlegungen im Übungsheft.
- Gib die Koordinaten der Punkte an, die du zur Berechnung der Steigung verwendest.
Zeichne den Graphen der proportionalen Funktion mit Hilfe eines Steigungsdreiecks!
- a)
- b)
Doping für Schnelle
Du liegst gut in der Zeit?
Dann versuch doch, den armen Radfahrern zu helfen...!
Damit die Radfahrer wissen, wie viel Doping sie zur Tour de France mitnehmen sollen, müssen sie wissen, welche Steigungen im Mittel zu erwarten sind.
Bearbeite dazu die im Übungsheft Aufgabe 6 auf Seite 34.
Du weißt nicht wie du anfangen sollst?
"mittlere Steigung" bedeutet dass man annimmt, die Steigung verläuft gleichmäßig zwischen zwei Punkten.
Gleichmäßige Steigung wiederum heißt, du kannst die beiden Punkte mit einer ________ verbinden...Legt man den Koordinatenusrprung in den Punkt A so gilt:
mittlere Steigungen
Alles geschafft? Super, dann auf zu Station 3!