.../Hefteintrag Flächeninhalt eines Kreises

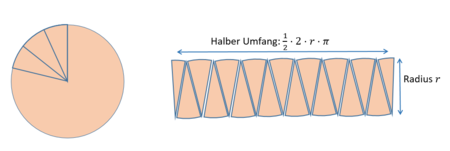
Übertrage den Merkekasten in dein Heft.

Merke

Wenn man sich einen Kreis in viele Stücke zerlegt denkt, kann man seinen Flächeninhalt aus Radius und Umfang berechnen. Für die Berechnung der Kreisfläche gilt dann:

$A= r^2 \cdot \pi$.

Übernehme auch die Skizze in dein Heft und ergänze deinen Hefteintrag um ein Beispiel.

Übungen

Aufgabe 2

Berechne die Kreisfläche. Runde auf zwei Nachkommastellen.

1. Der Radius des Kreises beträgt $r=3$cm.
2. Der Radius des Kreises beträgt $r=5$mm.
3. Der Radius des Kreises beträgt $d=12$cm.
4. Der Radius des Kreises beträgt $d=8$m.

Lösungen:

1. $A=(3cm)^2 \cdot \pi \approx 28,27cm^2$
2. $A= (5mm)^2 \cdot \pi \approx 78,54mm^2$
3. $A= (\frac{12cm}{2})^2 \cdot \pi \approx 113,1cm^2$
4. $A= (\frac{8m}{2})^2 \cdot \pi \approx 50,27m^2$

Aufgabe 3

Vergleiche die Pizzaangebote von Bella Italia. Bei welchem Angebot bekommt man am meisten Pizza für den günstigsten Preis?

Was kostet bei den drei Größen jeweils 1 cm² Pizza?

• kleine Pizza: $A=(9cm)^2 \cdot \pi \approx 254,47cm^2$, das sind bei einem Preis von 8,50€ etwa 3,3ct pro 1 cm² Pizza
• mittlere Pizza: $A=(12cm)^2 \cdot \pi \approx 452,39cm^2$, das sind bei einem Preis von 14€ etwa 3,1ct pro 1 cm² Pizza
• große Pizza: $A=(18cm)^2 \cdot \pi \approx 1017,87cm^2$, das sind bei einem Preis von 26,50€ etwa 2,6ct pro 1 cm² Pizza

Die große Pizza ist das günstigste Angebot. Die kleine Pizza ist im Vergleich etwas teurer als die mittlere Pizza.

zurück

Hier geht es zu Übungen rund um den Kreis

zurück

Hier geht es zu Übungen rund um den Kreis