Flächenberechnung von Rechteck und Quadrat: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(32 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Box|1=Lernpfad|2= Flächenberechnung von Rechteck und Quadrat |3=Lernpfad}}
{{Lernpfad-Navigation|
{{Lernpfad-Navigation|


Zeile 13: Zeile 10:
{{Box|Flächenmaße|Der Umfang ist eine Länge und wird mit Längenmaßen angegeben z.B. cm, dm, mm, .... Nun aber wird es um den Flächeninhalt gehen. In welcher Einheit eine Fläche angegeben wird, erfährst du beim Bearbeiten der nachfolgenden Aufgaben. |Arbeitsmethode}}
{{Box|Flächenmaße|Der Umfang ist eine Länge und wird mit Längenmaßen angegeben z.B. cm, dm, mm, .... Nun aber wird es um den Flächeninhalt gehen. In welcher Einheit eine Fläche angegeben wird, erfährst du beim Bearbeiten der nachfolgenden Aufgaben. |Arbeitsmethode}}
{{h5p-zum|id=9402|height=100}}
{{h5p-zum|id=9402|height=100}}
{{Box|Merke|Stoppe das Video von Folie 2 bei 2:10 und schreibe den Merktext ins Schulübungsheft. (Überschrift: Umwandlung von Flächenmaßen)
|Merksatz}}


{{Box|Geogebra Flächeninhalt|Sieh dir die Geogebra Datei an und experimentiere. Besprich mit einem Schulkollegen bzw. einer Schulkollegin, wie man die Fläche eines Rechtecks berechnen kann. https://www.geogebra.org/m/FexywbYW |Experimentieren}}
{{Box|Geogebra Flächeninhalt|Sieh dir die Geogebra Datei an und experimentiere. Besprich mit einem Schulkollegen bzw. einer Schulkollegin, wie man die Fläche eines Rechtecks berechnen kann. https://www.geogebra.org/m/FexywbYW |Experimentieren}}
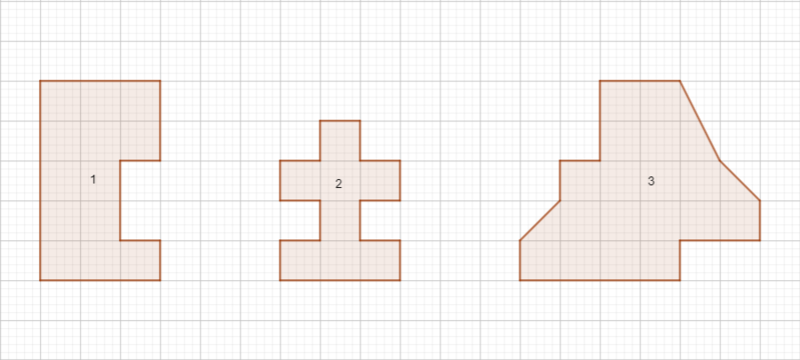
{{Box|Aufgabe|Ermittle entweder den Umfang u oder den Flächeninhalt A der Figuren. Ein Kästchen enstpricht der Größe eines Einheitsquadrates in cm<sup>2</sup>|Lösung}}
[[Datei:Umfang und Flächeninhalt unterscheiden.png|800px]]
<div class="lueckentext-quiz">
* Figur 1: A =  '''13()''' cm<sup>2</sup>
* Figur 2: u =  '''18()''' cm
* Figur 3: A =  '''19()''' cm<sup>2</sup>
</div>


{{Box|Video|Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an: https://studyflix.de/mathematik/flaecheninhalt-rechteck-2550 |Unterrichtsidee }}  
{{Box|Video|Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an: https://studyflix.de/mathematik/flaecheninhalt-rechteck-2550 |Unterrichtsidee }}  




{{Box|Merke|Scheibe den folgenden Merktext ins Geometrieheft. Überschrift: Flächeninhalt Rechteck und Quadrat.  
{{Box|Merke|Scheibe den folgenden Merktext ins Schulübungsheft. Überschrift: Flächeninhalt Rechteck und Quadrat.  


Jede Figur hat einen '''Flächeninhalt (A)'''. Das ist die Anzahl der Flächeneinheiten, die in der Fläche enthalten sind. Die Fläche eines Rechtecks wird berechnet mit der Formel:  
Jede Figur hat einen '''Flächeninhalt (A)'''. Das ist die Anzahl der Flächeneinheiten, die in der Fläche enthalten sind. Die Fläche eines Rechtecks wird berechnet mit der Formel:  


<math>A = a \times b </math>
<math>A = a * b </math>


[[Datei:Rechteck Fläche.png|250px]]
[[Datei:Rechteck Fläche.png|300px]]


|Merksatz}}
|Merksatz}}
Zeile 39: Zeile 52:
Die Fläche eines Quadrats wird berechnet mit der Formel:  
Die Fläche eines Quadrats wird berechnet mit der Formel:  


<math>A = a \times a </math>
<math>A = a * a </math>


[[Datei:Fläche Quadrat.png]]
[[Datei:Fläche Quadrat.png|250px]]


  |Merksatz}}
  |Merksatz}}




{{Box|Üben|Was musst du berechnen? Fläche oder Umfang? |Üben}}
{{Box|Üben|Textaufgaben. Versuche die Textaufgaben zu lösen. Zeige deine Ergebnisse anschließend der Lehrperson|Üben}}
Rechenaufgaben --> Was muss ich berechnen? Umfang oder Flächeninhalt? Ergebnis
 
# Ein rechteckiges Grundstück ist 43,3 m lang und 37,8 m breit. Bereche den Flächeninhalt des Grundstücks.
{{Lösung versteckt| 1636,74 m<sup>2</sup> |Lösung |Lösung}}
 
# Ein Fußballfeld kann verschieden groß sein. Die Länge beträgt zwischen 90 m und 120 m, die Breite zwischen 45 m und 90 m. Bestimme den Flächeninhalt des größtmöglichen und des kleinstmöglichen Fußballfeldes.
{{Lösung versteckt| 10800 m<sup>2</sup>;  4050  m<sup>2</sup>|Lösung |Lösung}}
 
# Ein quadratisches Grundstück mit einer Seitenlänge von 23,4 m soll mit Pflastersteinen ausgelegt werden. Berechne zuert den Flächeninhalt des Grundstücks. Berechne danach die Kosten für die Pflastersteine, wenn der Quadratmeterpreis 7,20 € beträgt und 5 Quadratmeter Pflastersteine als Reserve zusätzlich gekauft werden.
{{Lösung versteckt| Fläche: 547,56 m<sup>2</sup> Kosten: 3978,43 € |Lösung |Lösung}}
 
# Ein rechteckiges Grundstück wird verkauft. Das Grundstück ist 84 m lang und 72 m breit. Der Quadratmeterpreis beträgt 97,30€. Berechne den Grundstückspreis.
{{Lösung versteckt| 588 470,40 € |Lösung |Lösung}}
 
{{Fortsetzung|weiter=Expertenaufgaben für schnelle Rechenfüchse|}}

Aktuelle Version vom 24. Mai 2023, 06:10 Uhr

  1. Aktivierung des Vorwissens und Eigenschaften von Rechteck und Quadrat
  2. Konstruktionen von Rechteck und Quadrat
  3. Umfang von Rechteck und Quadrat
  4. Flächenberechnung von Rechteck und Quadrat
  5. Expertenaufgaben für schnelle Rechenfüchse

Flächenmaße
Der Umfang ist eine Länge und wird mit Längenmaßen angegeben z.B. cm, dm, mm, .... Nun aber wird es um den Flächeninhalt gehen. In welcher Einheit eine Fläche angegeben wird, erfährst du beim Bearbeiten der nachfolgenden Aufgaben.


Merke

Stoppe das Video von Folie 2 bei 2:10 und schreibe den Merktext ins Schulübungsheft. (Überschrift: Umwandlung von Flächenmaßen)

Geogebra Flächeninhalt
Sieh dir die Geogebra Datei an und experimentiere. Besprich mit einem Schulkollegen bzw. einer Schulkollegin, wie man die Fläche eines Rechtecks berechnen kann. https://www.geogebra.org/m/FexywbYW

Aufgabe
Ermittle entweder den Umfang u oder den Flächeninhalt A der Figuren. Ein Kästchen enstpricht der Größe eines Einheitsquadrates in cm2

Umfang und Flächeninhalt unterscheiden.png

  • Figur 1: A = 13() cm2
  • Figur 2: u = 18() cm
  • Figur 3: A = 19() cm2


Video
Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an: https://studyflix.de/mathematik/flaecheninhalt-rechteck-2550


Merke

Scheibe den folgenden Merktext ins Schulübungsheft. Überschrift: Flächeninhalt Rechteck und Quadrat.

Jede Figur hat einen Flächeninhalt (A). Das ist die Anzahl der Flächeneinheiten, die in der Fläche enthalten sind. Die Fläche eines Rechtecks wird berechnet mit der Formel:

Rechteck Fläche.png


Video
Sieh dir das Video zur Berechnung des Flächeninhalts eines Quadrats an: https://studyflix.de/mathematik/flaecheninhalt-quadrat-2552


Merke

Schreibe im bereits angefangenen Merktext weiter:

Die Fläche eines Quadrats wird berechnet mit der Formel:

Fläche Quadrat.png


Üben
Textaufgaben. Versuche die Textaufgaben zu lösen. Zeige deine Ergebnisse anschließend der Lehrperson
  1. Ein rechteckiges Grundstück ist 43,3 m lang und 37,8 m breit. Bereche den Flächeninhalt des Grundstücks.
1636,74 m2
  1. Ein Fußballfeld kann verschieden groß sein. Die Länge beträgt zwischen 90 m und 120 m, die Breite zwischen 45 m und 90 m. Bestimme den Flächeninhalt des größtmöglichen und des kleinstmöglichen Fußballfeldes.
10800 m2; 4050 m2
  1. Ein quadratisches Grundstück mit einer Seitenlänge von 23,4 m soll mit Pflastersteinen ausgelegt werden. Berechne zuert den Flächeninhalt des Grundstücks. Berechne danach die Kosten für die Pflastersteine, wenn der Quadratmeterpreis 7,20 € beträgt und 5 Quadratmeter Pflastersteine als Reserve zusätzlich gekauft werden.
Fläche: 547,56 m2 Kosten: 3978,43 €
  1. Ein rechteckiges Grundstück wird verkauft. Das Grundstück ist 84 m lang und 72 m breit. Der Quadratmeterpreis beträgt 97,30€. Berechne den Grundstückspreis.
588 470,40 €
Expertenaufgaben für schnelle Rechenfüchse
Abgerufen von „https://unterrichten.zum.de/index.php?title=Flächenberechnung_von_Rechteck_und_Quadrat&oldid=135015“