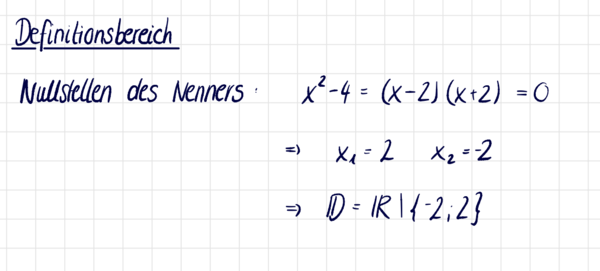Definitionsmenge: Unterschied zwischen den Versionen

Aktuelle Version vom 12. Dezember 2022, 09:36 Uhr

Für ganzrationale Funktionen ist die Definitionsmenge immer ganz $\mathbb{R}.$

Bei gebrochen rationalen Funktionen gibt es ggf. Definitionslücken bei den Nullstellen des Nenners.

Bestimme die Definitionsmenge der Beispielfunktion ${\displaystyle f(x)=\frac{x^3}{x^2-4} }$ im Heft.

@@ Zeile 1: / Zeile 1: @@
-Für ganzrationale Funktionen ist der Definitionsbereich immer ganz <math>\mathbb{R}.</math>
+Für ganzrationale Funktionen ist die Definitionsmenge immer ganz <math>\mathbb{R}.</math>
 Bei gebrochen rationalen Funktionen gibt es ggf. Definitionslücken bei den Nullstellen des Nenners.
+<span class="brainy hdg-ruler-pencil  fa-3x" "></span> Bestimme die Definitionsmenge der Beispielfunktion <math>f(x)=\frac{x^3}{x^2-4}
+</math>im Heft.
-{{Box||
+{{Lösung versteckt|[[Datei:Definitionsbereich.png|ohne|mini|600x600px]]|Lösung anzeigen|Lösung verbergen}}
-Definitionsbereich
-<math>x^2-4 = (x+2)(x-2) = 0
-</math><math>x_1= 2 \quad x_2=-2 </math><math>\Rightarrow</math>Definitionslücken bei  <math>x_1= 2 </math> und <math>x_2= -2 </math><math>\Rightarrow</math><math>\mathbb{D}=\mathbb{R}\setminus\{-2;2\}</math>|Unterrichtsidee }}
+<span class="brainy hdg-screen01  fa-3x" "></span>
+{{LearningApp
+| app = pv8yi5mcn22
+| height = 400px
+}}
+<br />
+{{Fortsetzung|vorher=zurück|vorherlink=Funktionsuntersuchung|weiter=Symmetrie|weiterlink=Symmetrieuntersuchung}}