Quantenphysik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| (115 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Einleitung== | ==Einleitung== | ||
Aussagen über quantenphysikalische Objekte werden mithilfe sehr komplizierter mathematischer Modelle getroffen, die weit über den Schulunterricht hinausgehen. Aber das gilt auch für die "klassischen" Forschungsbereiche der Physik, z.B. die {{wpde|Hamiltonsche_Mechanik|Hamiltonschen Bewegungsgleichungen}} oder die {{wpde|Navier-Stokes-Gleichungen}}, mit denen die Bewegungen von Gasen und Flüssigkeiten beschrieben werden. Im einen wie im anderen Fall kann man sich aber mit grafischen Darstellungen helfen, | Aussagen über quantenphysikalische Objekte werden mithilfe sehr komplizierter mathematischer Modelle getroffen, die weit über den Schulunterricht hinausgehen. Aber das gilt auch für die "klassischen" Forschungsbereiche der Physik, z.B. die {{wpde|Hamiltonsche_Mechanik|Hamiltonschen Bewegungsgleichungen}} oder die {{wpde|Navier-Stokes-Gleichungen}}, mit denen die Bewegungen von Gasen und Flüssigkeiten beschrieben werden. Im einen wie im anderen Fall kann man sich aber mit grafischen Darstellungen helfen, die von den Betrachtern intuitiv erfasst werden. | ||
Die Quantenphysik überrascht mit Begriffen, die aus der Perspektive der klassischen Physik sehr fremdartig wirken, z.B. {{wpde|Verschränkung}}, {{wpde|Tunneln}} und {{wpde|Unschärferelation}}. Man liest, mit der Quantenphysik sei der Zufall in die Physik eingebrochen, und sehr bekannt ist {{wpde|Albert Einsteins}} Widerstand gegen die Quantenphysik und seine zumeist verkürzt zitierte Formulierung: ''Gott würfelt nicht.''<ref>Albert Einstein schrieb 1926 in einem Brief an Max Born: | |||
''Die Quantenmechanik ist sehr achtunggebietend. Aber eine innere Stimme sagt mir, daß das noch nicht der wahre Jakob ist. Die Theorie liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher. Jedenfalls bin ich überzeugt, daß der nicht würfelt.'' | |||
Näheres siehe: https://de.wikipedia.org/wiki/Gott_w%C3%BCrfelt_nicht</ref> Aber den Zufall kann auch die klassische Physik nicht vertreiben, denn in ihr sind physikalische Messwerte als {{wpde|reelle Zahlen}} definiert; das sind Zahlen mit unendlich vielen regellos auftretenden Stellen hinter dem Komma, die niemals wirklich genau erfasst werden können. Das hat zur Folge, dass Voraussagen - beispielsweise über das {{wpde|Wetter}} - immer nur für eine begrenzte Zukunft zuverlässig sein können, denn irgendwann werden die feinen Unterschiede, die man nicht hat messen können, für die weitere Entwicklung ausschlaggebend sein.<ref>Siehe dazu Ilya Prigogine, Isabelle Stengers: ''Dialog mit der Natur'' München (Piper) deutsch 6. Aufl. 1990; sieselben: ''Das Paradox der Zeit'' deutsch München (Piper) 1993.</ref> | |||
Dieser Lernpfad zur Quantenphysik möchte zweierlei vermeiden: | |||
*Es geht nicht darum, Mathematische Methoden zu vermitteln, die man sich mit der Schulmathematik nicht erarbeiten kann. Für Physikstudenten steht ja eine reiche Auswahl an Lehrbüchern bereit.<ref>Meine Lehrbücher waren: | |||
Gerhard Gerlich: ''Eine neue Einführung in die statistischen und mathematischen Methoden des Quantentheorie'', Braunschweig (vieweg) 1977 | |||
Das Vorlesungsskript von Heinrich Mitter ''Quantentheorie'' Mannheim (BI Hochschultaschenbücher) 1969, das heute [https://docplayer.org/13447805-Heinrich-mitter-quantentheorie-vorlesungen-ueber-theoretische-physik-iii.html Online zur Verfügung steht]. Die legendären Vorlesungen von Richard Feynman (1918-1988) stehen heute ebenfalls in der Bearbeitung seiner Schüler online zur Verfügung: https://www.feynmanlectures.caltech.edu/</ref> | |||
*Es ist mir zu wenig, nur die Phänomene zu benennen ohne die logischen Konzepte, die ihrer mathematischen Beschreibung zugrundliegen. Wer diese nicht berechnen kann, kann doch wenigstens ihre grafische Veranschaulichung erfassen und so ein gewisses Verständnis erzielen. Dazu braucht man einen Einstieg, und den habe ich gewählt bei der Frage: '''Was ist eine Messung?''' Denn das unterscheidet seit {{wpde|Galileo Galilei|Galileo Galileis}} Zeiten Physik von alltäglichem Hinschauen: '''Die zahlenmäßige Erfassung eines Ausschnittes der Wirklichkeit mit dem Ziel der Berechnung der Zusammenhänge.''' | |||
==Eine Messung== | |||
Vor einiger Zeit – ich bin nicht stolz darauf - bekam ich von der Stadt Grünberg einen Brief, aus dem ich einen Ausschnitt zeige: | |||
[[Datei:Bussgeldbescheid.JPG]] | |||
Über die Messung, die in diesem Fall durchgeführt worden ist, stehen im Bescheid einige für unser Thema relevante Informationen: | |||
*Es sind Laserstrahlen hergestellt worden, deren spezifische Eigenschaft, {{wpde|Kohärenz}}, nur mit Mitteln der Quantenphysik verstanden werden kann. Und das kann man verallgemeinern: Gleichgültig ob wir mit Hilfe von Licht etwas "sehen", mithilfe chemischer Prozesse etwas "schmecken" oder "riechen" oder ob wir mechanische Reizungen "fühlen" oder "hören" - immer ist die Quantenphysik im Spiel. | |||
*Eine klassische Messgröße, die Geschwindigkeit eines Fahrzeugs, konnte zu einem bestimmten Zeitpunkt an einem bestimmten Ort mit so großer Genauigkeit festgestellt und der Person des Autofahrers zugeordnet werden, dass mir kein Gericht Recht geben wird, wenn ich meine Ordnungswidrigkeit leugnen wollte. Deshalb wird es am einfachsten und risikoärmsten sein, den Bußgeldbescheid zu bezahlen. | |||
{{Box|Aufgabe| | |||
* Benenne ein anderes Beispiel einer Messung | |||
* Beschreibe möglichst exakt, was derjenige tut, der die Messung durchführt. | |||
* Versuche, die quantenphysikalischen Objekte zu benennen, die in dem Messvorgang beteiligt sind (z.B. Licht, Chemie) | |||
* Gib an, welche Konsequenzen die Messung hat, wie genau sie dazu sein muss und welche Folgen Fehler haben können. | |||
|Aufgabe}} | |||
[[Datei:Klassische Messung.jpg|750px]] | |||
{{Box|Details| | |||
Wir machen uns klar, was bei der {{wpde|Lidar|Geschwindigkeitsmessung mit einem Lasergerät}} passiert: | |||
* Das Messgerät beschießt das fahrende Auto mit Lichtteilchen, von denen einige so reflektiert werden, dass sie zum Messgerät zurückkehren, welches automatisch die Geschwindigkeit bestimmt. | |||
* Das Auto wird fotografiert und anhand des Nummernschildes identifiziert, sodass der Strafzettel den richtigen Autobesitzer erreicht, und das Foto ermöglicht die Identifikation des Fahrers. | |||
* Weil masselose Lichtteilchen, verglichen mit einem tonnenschweren Auto, sehr wenig Energie transportieren, kann man im Falle einer Verkehrskontrolle davon ausgehen, dass die Messmethode die gemessene Geschwindigkeit nicht beeinflusst und weder das Nummerschild noch das Portraitfoto manipuliert. | |||
|Kurzinfo}} | |||
{{Box|Zum Nachdenken| | |||
Was ändert sich, wenn das Beobachtungsobjekt kein tonnenschweres Auto ist, sondern eines des leichtesten, kleinsten, flüchtigsten Teilchen der Natur? | |||
|Aufgaben}} | |||
{{H5p-zum|id=13167|height=232}} | |||
==Das Atom== | |||
{{Box|Historisches| | |||
{{wpde|Empedokles}} aus Agrigent (495-435 v.C.) hatte den Philosophenstreit, ob alle Dinge nun aus dem Wasser, dem Feuer oder dem Hauch entstanden seien, dadurch beendet, dass er alle vier '''''Elemente''''' - Erde, Wasser, Feuer und Luft (heute sprechen wir von {{wpde|Aggregatzustand|Aggregatzuständen}}) - zu Grundbestandteilen allen Daseins erklärt hatte. | |||
{{wpde|Demokrit}} von Abdera (460-370) baute auf diesen Überlegungen auf und postulierte, die vier Elemente müssten aus unteilbaren Teilchen bestehen, die er ''atomoi'' nannte, zu deutsch: ''Unteilbare'' <Teilchen>. Er stellte sich diese Atome als winzig kleine geometrisch sehr regelmäßige "Bauklötzchen" vor: Kugeln, Würfel, Zylinder, Kegel, die sich im vollkommen leeren Raum bewegen. Später hat man {{wpde|platonischer Körper|die fünf regelmäßigen ''platonischen'' Körper}} den Elementen zugeordnet: der Erde den Würfel, dem Wasser den Ikosaeder, der Luft den Oktaeder und dem Feuer die Pyramide. Der Dodekaeder sollte die Himmelsmaterie bilden, die ''fünfte essentia, von deren Natur wir nichts wissen''. | |||
|Kurzinfo}} | |||
{{Box|Kritik| | |||
Schon {{wpde|Aristoteles}} aus Stagira (399-322) kritisierte die Atomtheorie, weil er Bewegung in einem vollkommen leeren Raum für unmöglich hielt. Auch konnte sich niemand vorstellen, wie die ''Atome'' Kontakt miteinander aufnehmen und sich zu größeren Körpern verbinden sollten. Sie können ja keine "Ärmchen" haben, mit denen sich sich "unterhaken". | |||
|Hervorhebung}} | |||
{{Box|Aufgabe| | |||
Denke darüber nach, | |||
* warum die Atomtheorie des Demokrit so verführerisch ist, | |||
* und warum es nicht stimmen kann, dass die Welt aus lauter "Bauklötzchen" besteht, die wir wegen ihrer Kleinheit nie zu sehen bekommen und warum das auch unbefriedigend wäre. | |||
|Aufgabe}} | |||
[[Datei:Kanonenmessung.jpg|750px]] | |||
{{Box|Gedankenexperiment| | |||
Stell Dir vor, du gehörst zu einer Riesenwelt. Für die Riesen sind Objekte von der Größenordnung von Autos das Kleinste, was sie wahrnehmen können. | |||
* Was können die Riesen tun, um etwas über Autos herauszufinden? | |||
* Was werden sie nie herausbekommen können? | |||
|Experiment}} | |||
Die Riesen könnten eine aus ihrer Perspektive winzige Kanone herstellen und die Autos damit beschießen. Aus unserer Zwergenperspektive wird nach der Kollision nichts mehr sein, wie es war: | |||
*Kugel und Auto werden sich zu Trümmerteilen verformen. | |||
*Ihre Geschwindigkeiten und Bewegungsrichtungen werden sich stark verändern. | |||
Die Riesen sehen nur punktförmige Objekte, die sich z.B. auf einem Fotosensor bemerkbar machen. Wenn sie das Experiment mit verschiedenen Parametern durchführen, können sie sicher etwas über die Masse und die Geschwindigkeit der beteiligten Objekte sagen und den Ort der Kollision bestimmen. | |||
[[Datei:Gedankenexperiment Hindernis.jpg|750px]] | |||
Die Riesen könnten das Verhalten von Autos auch an fest montierten Objekten studieren und feststellen, dass die Objekte vor dem Objekt stehen bleiben oder es mit reduzierter Geschwindigkeit passieren. Welchen Reim werden sie sich darauf machen? | |||
{{Box|Schlussfolgerung| | |||
Diese Riesen werden niemals Bußgeldbescheide verschicken. | |||
* Da für sie Autos unteilbar sind, können sie in und an ihnen weder Fahrer noch Nummernschild sehen und das einzelne Auto nicht identifizieren und nachverfolgen. | |||
* Wem sollten sie Bußgeldbescheid schicken, denn das Auto ist nach der Kollision kaputt, und der Fahrer wird nicht mehr in der Lage sein, Strafe zu zahlen. | |||
|Hervorhebung}} | |||
==Wasserstoff== | |||
Die "Kanonenkugeln" der Quantenphysiker sind Photonen, übersetzt etwa ''Lichtteilchen''. {{wpde|Photon|Photonen}} übermitteln nicht nur das Licht, sondern auch Wärme und Radiosignale, Röntgen- und Gammastrahlen. Zwei unserer fünf Sinne, Tastsinn und Gehör, verarbeiten mechanische Signale. Damit eine Wahrnehmung zustandekommt, müssen die Schallwellen und Texturen zuerst in chemische und elektrische Signale verwandelt werden, und dabei spielen wieder die Photonen eine Rolle. Der Gesichtssinn wandelt Photonen durch die Netzhaut direkt in Signale um, die das Nervensystem verarbeiten kann; Geruch und Geschmack verarbeiten chemische Eigenschaften der Stoffe, die von der Nasenschleimhaut oder der Zunge durch Photonenaustausch erfasst werden. | |||
Aber wir sehen und riechen '''mithilfe''' der Photonen. Wir nehmen die Lichtteilchen selbst '''nicht''' wahr, und wir reden über die wahrgenommenen Objekte, nicht über die Mechanismen der Wahrnehmung. Wir sagen: ''Die Rose ist rot'' oder ''Die Suppe ist zu salzig'', ohne uns Gedanken darüber zu machen, auf wie komplizierten Wegen die Information über die Objekte zu uns gekommen ist. | |||
Diese Ignoranz können sich Atomforscher nicht leisten. Sie benötigen eine Theorie des Lichtes, um ermitteln zu können, was sie mithilfe des Lichtes in der atomaren Welt „sehen“. | |||
{{Box|Voraussetzung| | |||
Zwei Elemente der Licht-Theorie werden unten vorausgesetzt: | |||
* Jedes Lichtteilchen transportiert {{wpde|Energie}}. | |||
* Die Energie ist proportional zu seiner {{wpde|Frequenz}} und umgekehrt proportional zur {{wpde|Wellenlänge}}. | |||
|Definition}} | |||
Das „Haustier“ der Quantenphysiker ist der {{wpde|Wasserstoff}}. {{wpde|Antoine Laurent de Lavoisier}} (1743-1794) hat dem Gas seinen Namen gegeben. {{wpde|Dmitri Iwanowitsch Mendelejew}} (1834-1907) wies ihm einen Platz in seinem {{wpde|Periodensystem}} zu: Ein reaktionsfreudiges Element mit dem leichtesten Atomgewicht von allen und der Ordnungszahl 1, weil nur ein Proton seinen Atomkern bildet. | |||
Da man dem Wasserstoffatom einen elektrisch negativ geladenen Bestandteil klauen kann, stellen wir es uns vor als "Zusammensetzung" aus einem positiv geladenen Teil – {{wpde|Proton}} genannt – und aus einem negativ geladenen – dem {{wpde|Elektron}}. Solche Wörter aus der Alltagssprache gehören in der Quantenphysik in Anführungszeichen, denn wenn ein Objekt unserer Alltagswelt aus mehreren kleineren "zusammengesetzt" ist, dann sind wir daran gewöhnt, das Objekt mit Schere, Messer, Schrauber oder Stemmeisen "zerlegen" zu können. Auch das Wasserstoffatom kann "zerlegt" werden, aber nicht, indem man ein Instrument "zwischen" Elektron und Proton bringt, sondern nur, indem man das Elektron "lockt". | |||
Wie sich Proton und Elektron im Wasserstoffatom verhalten, konnte die Quantenphysik aufklären, und das gehört zu ihren brillantesten Leistungen. Im Folgenden werden einige Aspekte der Theorie qualitativ dargestellt. Die mathematischen Rechenvorschriften der Theorie können im Bild veranschaulicht werden. Aus solchen Abbildungen geht zwar nicht hervor, wie die Physiker darauf gekommen sind, aber man kann damit schon erläutern, was sie meinen. | |||
[[Datei:Wasserstofflampe.jpg]] | |||
{{Box|Experiment| | |||
Um Wasserstoff besser kennen zu lernen, wird etwas Gas isoliert, in ein Röhrchen eingeschlossen und von beiden Seiten unter Strom gesetzt. | |||
Was, glaubst Du, wird geschehen? | |||
Wenn Druck und Spannung stimmen, wird das Gas blau-violett leuchten. Warum? | |||
|Experiment}} | |||
[[Datei:Wasserstofflampe Prinzip.jpg]] | |||
Wasserstoff besteht aus Ladungsträgern, positiv geladenen Protonen und negativ geladenen Elektronen. Wenn der Strom fließt, werden geladene Partikel vom gegensätzlich geladenen Pol angezogen und sich dahin auf den Weg machen. Es wird zu Rempeleien mit den Wasserstoffatomen kommen, die Elektronen werden entweder ganz aus dem Atom geschlagen oder auf eine andere Bahn um das Proton geworfen. Da bewegte geladene Partikel elektromagnetische Strahlung aussenden, erklärt sich so das Licht. | |||
"{{wpde|Licht}}" nennen wir den Teil elektromagnetischer Strahlung, den wir sehen können. Denn die Lichtteilchen, die die elektromagnetische Strahlung transportieren, unterscheiden sich darin, wieviel Energie sie mitbringen, die - wir erinnern uns - mit der Frequenz und der Wellenlänge zusammenhängt. | |||
[[Datei:Sichtbares Spektrum.jpg]] | |||
{{Box|Information| | |||
Licht ändert beim Übergang von Luft in Glas oder Wasser seine Richtung ein wenig; man sagt, es wird gebrochen. Lässt man Licht durch ein {{wpde|Prisma (Optik)|Prisma}} fallen, werden nicht alle Farben (mitdenken: Frequenzen, Wellenlängen) um den gleichen Winkel umgelenkt, sondern das Licht spaltet sich auf in seine Spektralfarben. Das {{wpde|Spektrum (Physik)|Spektrum}} einer Glühlampe oder der Sonne sieht dann so aus wie das Bild oben, das uns als Himmelserscheinung vertraut ist: der {{wpde|Regenbogen}}. | |||
Das Licht, das wir sehen können, hat eine Frequenz von höchstens 780 Terahertz; das entspricht einer Wellenlänge von 380 Nanometern und der Farbe blauviolett links, und es hat eine Frequenz von mindestens 785 Terahertz und eine Wellenlänge von 780 Nanometern; das ist das purpurrote Licht rechts. Dazwischen liegen alle anderen Farben in einer bestimmten Reihenfolge: Man spricht vom Farbenspektrum. | |||
|Kurzinfo}} | |||
Kommen wir zurück zur Wasserstoff-Entladungslampe. | |||
{{Box|Experiment| | |||
Man kann das Licht der Wasserstofflampe durch ein Prisma aufspalten, wie wird das aussehen? | |||
Wenn wir an die Rempelei zwischen den verschiedenen Ladungsträgern in dem Gas zurückdenken, dann müssten die erzeugten Photonen alle möglichen Energiebeträge mitnehmen: Manche Atome werden mittig getroffen; da knallts heftig, andere werden nur in einem mehr oder weniger flachen Winkel gestreift; da entsteht wenig Lichtenergie. Wir erwarten also ein kontinuierliches Farbenspektrum, vielleicht in dem Wellenlängenbereich ein wenig schmäler als das weiße Sonnenlicht; so könnte man die Farbigkeit der Wasserstofflampe erklären. | |||
|Experiment}} | |||
[[Datei:Wasserstoffspektrum mit Messwerten.jpg]] | |||
Was tatsächlich passiert ist etwas völlig anderes: Das Spektrum des Wasserstoffes besteht aus scharfen Linien und die dazwischenliegenden Farben kommen nicht vor. | |||
Schon 1888 formulierte der schwedische Physiker {{wpde|Johannes Rydberg|Janne Rydberg}} eine Formel, aus der man die Linien ableiten kann. Aber damit war natürlich noch nicht erklärt, warum das Wasserstoffspektrum nicht kontinuierlich ist, sondern aus Linien besteht, die eine mathematisch ableitbare Regelmäßigkeit besitzen. | |||
==Quantenphysikalische Zustände== | |||
[[Datei:Atommodelle_Thomson_Rutherford.jpg|800px]] | |||
{{Box|Historisches| | |||
{{wpde|Joseph John Thomson}} stellte sich 1903 das Atom nach Art eines Rosinenkuchens vor: Die Elektronen sollten sich im Proton aufhalten wie Rosinen in einem Rosinenkuchen, im Wasserstoffatom eine einzige Rosine, im Goldatom 79 Stück. | |||
{{wpde|Ernest Rutherford}} argumentierte, dass es dann nur eine Spektrallinie geben dürfte. Er konstruierte 1911 ein planetarisches Atommodell, nach dem sich die Elektronen um den Atomkern bewegen wie Planeten um ihre Sonne. | |||
|Kurzinfo}} | |||
{{H5p-zum|id=13471|height=232}} | |||
Die Physiker mussten sich also im ersten Viertel des 20. Jahrhunderts etwas vollkommen Neues überlegen. Dabei mussten sie eine Voraussetzung aufgeben, die bis dahin selbstverständlich hingenommen worden war, nämlich, dass alle physikalischen Objekte ''anschaulich'' sind. | |||
{{Box|Definition Anschaulichkeit| | |||
Unsere gesamte Wahrnehmung und unsere Handlungsmöglichkeit beruhen darauf, | |||
* dass wir uns in einer Zeit befinden, die von ''gestern'' nach ''morgen'', von ''eben noch'' bis ''jetzt gleich'' dahinfließt, | |||
* dass wir uns in einem Raum bewegen, in dem sich ''vorne'' und ''hinten'', ''oben'' und ''unten'', ''rechts'' und ''links'' voneinander unterscheiden lassen. | |||
* Zeit und Raum können wir durch Koordinatensysteme abbilden und allem, was sich darin befindet, durch reelle Zahlen einen Ort zuweisen. (Wir wissen, dass wir die reellen Zahlen nicht ''vollkommen genau'' messen können; aber für die praktischen Erfordernisse messen wir ''genau genug'', um zum Beispiel einen Satelliten sicher zum Mond zu bringen und wieder zurück. | |||
Die Anschaulichkeit ist ''Bedingung der Möglichkeit'' von Erfahrung und Handeln, wie {{wpde|Immanuel Kant}} in seiner Kritik der reinen Vernunft 1781 nachgewiesen hat. Allerdings sind weder die Welt insgesamt, noch ihre kleinsten Teilchen in einem anschaulichen Modell widerspruchsfrei zu beschreiben; das hat Kant auch bewiesen. | |||
|Definition}} | |||
===Welle-Teilchen-Dualismus=== | |||
Die Physik der Neuzeit hat mathematische Methoden entwickelt, um die verschiedenen Phänomene, die uns umgeben, zahlenmäßig zu erfassen (Messung) und zu berechnen: | |||
*Die '''Physik des Massenpunktes''' beschreibt Bewegungen, die man mit hinreichender Genauigkeit als Bewegungen eines punktförmigen Objektes ansehen kann (z.B. der Schwerpunkt einer Kugel). Zu diesem Formalismus gehören Begriffe wie Geschwindigkeit, Beschleunigung, Impuls, kinetische Energie. An einem bekannten Experiment zur Impulserhaltung, dem Verhalten der {{wpde|Kugelstoßpendel|Newtonwiege}} soll die Konzeption exemplarisch verdeutlicht werden. | |||
{{Box|Experiment| | |||
Die Newtonwiege besteht aus fünf gleich schweren Kugeln, die an gleich langen Fäden aufgehängt sind. | |||
Unter einem elastischen Stoß versteht man einen Zusammenstoß, bei dem (fast) keine Bewegungsenergie verloren geht. Dadurch kann bei der Newtonwiege die Impulserhaltung (Impuls gleich Masse mal Geschwindigkeit) besonders gut demonstriert werden. (Ein Kaugummi, an der richtigen Stelle auf eine Kugel geklebt, würde das Experiment völlig verändern.) Schau Dir jetzt die Experimente mit der Newtonwiege an und suche Dir wenigstens zwei davon aus, um die Impulserhaltung zu beschreiben. | |||
{{#ev:youtube|oKUvaYrQJCs}} | |||
|Experiment}} | |||
*Die '''Physik der Schwingungen und Wellen''' beschreibt Erscheinungen, die nur in größeren Ansammlungen von Materie auftreten. Zum Beispiel wird ein ins Wasser geworfener Stein Wellen erzeugen, das sind periodische Veränderungen der Wasserhöhe. Wenn du in eine Blockflöte bläst und Schallwellen erzeugst, entstehen periodische Druckschwankungen. Zur Physik der Schwingungen und Wellen gehören folgende Begriffe: | |||
**Frequenz (Zahl der Wellen pro Zeiteinheit) | |||
**Amplitude (Intensität der Schwingung) | |||
**Resonanz (Mitschwingen eines dazu fähigen Objektes) | |||
**Interferenz (Schwingungmuster, das durch die gegenseitige Beeinflussung zweier Wellen entsteht) | |||
Wer sich den Begriff "Interferenz" detailliert beschreiben lassen will, sieht sich folgendes Video an: | |||
{{#ev:youtube|__1Dyh6frwE}} | |||
Welle-Teilchen-Dualismus bedeutet nun, dass man zur Beschreibung eines Quantensystems (z.B. ein Elektron im Wasserstoffatom) '''die beiden Formalismen zur Berechnung eines Teilchens (Massenpunktes) und einer Welle in einem Formalismus zusammenfasst.''' | |||
===Komplexe Zahlen=== | |||
Die Mathematik hat ihre liebe Not mit den Umkehroperationen. | |||
Solange ich addiere und multipliziere, kann ich sicher sein, dass ich ein gültiges Ergebnis herausbekomme: 5 + 3 = 8 und 5 * 3 = 15. Das ist kinderleicht. Das funktioniert immer, egal, mit welchen beiden natürlichen Zahlen ich diese Operation durchführe. Nun sind wir aber vorwitzig und wollen zum Beispiel auch solche Fragen beantworten: Mit welcher Zahl muss ich 5 multiplizieren, um 15 herauszubekommen? Das ist immer noch einfach 15 / 5 = 3. Aber wenn ich mir diese Aufgabe stellen kann, kann ich auch eine andere Aufgabe hinschreiben: 15 / 0 = ? Gut, aufschreiben kann ich die Aufgabe, aber Sinn hat sie keinen. Wenn ich 15 Orangen habe und unter 3 Leuten aufteilen soll, kriegt jeder fünf. Wenn ich sechs Orangen habe und unter vier Leuten aufteile, muss ich zwei in der Mitte durchschneiden, und jeder bekommt eine ganze und eine halbe. Das hat alles Sinn. Aber wenn ich 15 Orangen habe und niemand da ist, der etwas davon kriegen soll, wie viel kriegt dann keiner? Das macht keinen Sinn. Also sollten wir die Aufgabenstellung "15 / 0" einfach verbieten. | |||
Eine Ebene höher geht es darum, Zahlen einmal oder öfter mit sich selbst zu multiplizieren. Die Umkehrfrage lautet dann zum Beispiel: Welche Zahl muss ich mit sich selbst multiplizieren, um 1 herauszubekommen? - Die Antwort ist leicht zu finden, denn 1 * 1 = 1. Aber diese Antwort ist nicht ausreichend, denn -1 * -1 = 1 gilt (Man erinnert sich ''Minus mal Minus gibt plus.'') ebenfalls. Es gilt also: | |||
<math>\surd 1 = 1 und \surd 1 = -1</math> | |||
Was ist jetzt, wenn wir die Aufgabe niederschreiben: "<math>\surd -1 = ?</math> ?" | |||
Wir können auch diese Aufgabenstellung einfach verbieten. Aber große Mathematiker wie {{wpde|Gerolamo Cardano}} (1501-1576) und {{wpde|Carl Friedrich Gauß}} (1777-1855) probierten aus, was passiert, wenn man der Aufgabe eine Lösung zuordnet durch die Definition: | |||
<math>\surd -1 = i</math> oder andersherum i * i = -1 | |||
Während eine ''reelle Zahl'' als Punkt auf einer ''Zahlengeraden'' vorgestellt wird, entsteht jetzt eine Zahlenebene: Eine ''komplexe Zahl hat also zwei Komponenten: Den gewöhnlichen reellen Anteil und einen ''imaginären Anteil'', eine reelle Zahl, multipliziert mit der imaginären Einheit <math>i = \surd -1</math>.'' | |||
[[Datei:KomplexeZahlen.jpg]] | |||
{{Box|Wichtig| | |||
Quantenphysikalische Zustände werden mit komplexen Zahlen beschrieben. Auf diese Weise hat man etwas mehr Platz, die Physik der Wellen und die Physik der Massenpunkte zusammen in den Zustandsgleichungen unterzubringen. Anderseits verzichtet man durch die komplexen Funktionen auf die Anschaulichkeit, denn Messergebnisse im Raum unserer Wahrnehmungen sind reell und nicht komplex. | |||
|Merksatz}} | |||
===Kohärenz=== | |||
Es hat ein bisschen gedauert, aber jetzt sind die Elemente zusammen, die gebraucht werden, um das Spektrum des Wasserstoffs zu interpretieren. Wie sich Elektronen in der Nähe des Atomkerns verhalten, können diejenigen, die sich damit auskennen, aus der {{wpde|Schrödinger-Gleichung}} ableiten. Die folgende Zeichnung veranschaulicht zwei Lösungen der Gleichung: | |||
[[Datei:Kugelsymmetrische Orbitale.jpg]] | |||
{{Box|Aufgabe| | |||
Schau Dir die Veranschaulichung in Ruhe an und gib Dir Rechenschaft darüber, was zu sehen ist. | |||
|Aufgabe}} | |||
'''Eigenschaften eines kohärenten Quantensystems''' | |||
#Das Bild ist '''nicht etwa ein Foto''' eines Wasserstoffatoms. Denn ein ungestörtes Atom sendet kein Licht aus und hat keinerlei Wechselwirkung mit seiner Umgebung. | |||
#Mathematisch kommt das darin zum Ausdruck, dass die Funktionswerte komplexe Zahlen sind, Messwerte aber relle Zahlen sein müssen. Diese komplexen Zahlen veranschaulicht die Zeichnung. | |||
#Im Wellenbild des Elektronenzustands kann man die Intensität der Färbung als Amplitude (Auslenkung) der Welle interpretieren. | |||
#Im Teilchenbild entspricht die Farbintensität der Wahrscheinlichkeit, dass sich das Elektron an dieser Stelle aufhält. | |||
#Anders als in Gleichnungen der klassischen Physik kommt in quantenphysikalischen Zustandsgleichungen das Plancksche Wirkungsquantum h = 6,23 * 10 <sup>-34</sup> Joule * Sekunde vor. Das ist die kleinste mögliche Wirkung, die ein physikalisches System auf seine Umgebung ausüben kann. | |||
#Ebenfalls neu ist, dass in quantenphysikalischen Gleichungen ganze Zahlen vorkommen, die Quantenzahlen. Die beiden oben abgebildeten Orbitale unterscheiden sich in der Hauptquantenzahl, die den Abstand zum Atomkern bestimmt. Die kleinste Elektronenschale hat die Hauptquantenzahl n=1, die nächstgrößere n=2 usw. | |||
#In der innersten Schale, in der das Elektron sich innerhalb von einem Zehnmilliardstel Millimeter um den Atomkern aufhält, ist nur Platz für ein einziges kugelsymmetrisches Orbital. | |||
#In den größeren Schalen ist mehr Platz. Das drückt sich darin aus, dass die Nebenquantenzahl, die Form und Symmetrieeigenschaften eines Orbitals bezeichnet, höchstens l=n-1 sein kann. Die Magnetquantenzahl wiederum kann m=-l, .. m=0 .. , m=l sein und bezeichnet die Ausrichtung der Symmetrieachse des Orbitals im Raum. | |||
#Unten ist ein hantelförmiges Orbital veranschaulicht, dessen Symmetrieachse von oben nach unten geht, es gibt zwei weitere so geformte Orbitale mit der Symmetrieachse von rechts nach links oder von vorne nach hinten durch die Bildebene. Zusammen mit dem kugelförmigen Orbital wird die zweite Schale also von insgesamt vier Orbitalen ausgefüllt. In der dritten Schale ist logischerweise noch mehr Platz für weitere Orbitalformen. | |||
#Im Wasserstoffatom gibt es nur ein Elektron, das sich in einem der Orbitale befinden kann, je nachdem wie viel Bewegungsenergie es hat. In den größeren Atomen können in jedem Orbital zwei Elektronen Platz finden, die sich im Spin unterscheiden, denn der kann s = + 1/2 oder s = -1/2 betragen. | |||
#Die Pauli-Regel sagt nämlich, dass sich alle Elektronenzustände in einem System in mindestens einer der vier Quantenzahlen n, l, m und / oder s unterscheiden müssen. | |||
#Das {{wpde|Periodensystem}} der chemischem Elemente lässt sich in seinem Aufbau dadurch erklären, dass die Elektronen, deren Zahl die {{wpde|Ordnungszahl}} des jeweiligen Elementes bestimmt, nacheinander die Orbitale auffüllen, die jeweils die geringste Bewegungsenergie besitzen. | |||
[[Datei:POrbital.jpg]] | |||
Ein gut zu verstehender Film erläutert das System der Quantenzahlen: | |||
{{#ev:youtube|X9U0Obzs5lQ}} | |||
===Messung (Störung)=== | |||
Wie schön und elegant ein physikalisches Modell auch sein mag, Physik wird erst daraus, wenn wir die Objekte des Modells nötigen können, Spuren in unserer Wahrnehmungswelt zu hinterlassen: Ausschläge eines Messgerätes, Spuren auf einem Foto oder eben Spektrallinien. | |||
{{Box|Denke nach| | |||
Bei der Betrachtung der Spektrallinien einer Wasserstoffgasentladung hatten wir uns darüber gewundert, dass es kein regenbogenartiges kontinuierliches Spektrum gibt, sondern diskrete Linien. | |||
Wenn du die Eigenschaften des kohärenten Quantenzustandes eines Elektrons in der Umgebung des Wasserstoffatoms noch einmal durchdenkst, kannst du dann diesen erstaunlichen Befund erklären? | |||
|Aufgabe}} | |||
[[Datei:Wasserstoffspektrum mit Messwerten.jpg]] | |||
{{Box|Erklärung| | |||
Die Vorstellung, was in dem stromdurchflossenen Glasrohr mit Wassestoffgas passiert, brauchen wir kaum zu korrigieren: Zwischen den zu den elektrischen Polen eilenden Ladungsträgern und den Wasserstoffatomen kommt es zu einer Rempelei, bei der die Elektronen aus der Bahn geworfen werden. | |||
Allerdings können sich die Elektronen nicht frei bewegen, sondern nur in den durch die Quantenzahlen festgelegten Orbitalen (es sei denn, die Bewegungsenergie reicht aus, das Elektron ganz vom Atomkern zu trennen.) | |||
Wenn die Elektronen dann vom Atom eingefangen werden oder von einer äußeren Schale (mit mehr Bewegungsenergie) auf eine weiter innen liegende "herunterfallen", geben sie die Energiedifferenz an ein Lichtteilchen, ein Photon ab. | |||
|Definition}} | |||
Einzelheiten: | |||
#Eine violette Linie bei einer Wellenlänge 410,2 nm entsteht, wenn das Elektron vom Atom eingefangen wird und das Orbital n = 2 besetzt. | |||
#Die blauviolette Linie bei der Wellenlänge 431 nm entsteht, wenn das Eletron von der Schale n = 5 auf die Schale n = 2 abstürzt. | |||
#Die blaugrüne Linie (486 nm) sendet ein Eletron aus, das vom Orbital n = 4 auf das Orbital n = 2 herunterfällt. | |||
#und die rote Linie (656,3 nm) sendet ein Elektron aus, das vom Orbital n = 3 zum Orbital n = 2 übergeht. | |||
#Wenn Elektronen auf das niedrigste Energieniveau (n = 1) herabfallen, wird so viel Energie frei, dass ultraviolette Strahlung entsteht, die wir mit bloßem Auge nicht sehen können. | |||
Die Universität Wuppertal bietet auf ihrer Seite eine detailliertere Erklärung an. <ref>http://www.hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/hyde.html#c4</ref> | |||
{{Box|Wie kann man die Messung mathematisch definieren?| | |||
Wellenfunktionen sind komplexe Funktionen, die Zustände in der Natur beschreiben, die niemand je zu sehen bekommt. | |||
Setzt man aber die Funktionen ins Quadrat, was passiert dann mit dem komplexen Anteil? | |||
|Frage}} | |||
{{Box|Quadratur des Rätsels| | |||
Ganz einfach: Da nach Definition i mal i gleich -1 ist, verschwindet der komplexe Anteil, und man erhält eine relle Zahl, die man als Messergebnis interpretieren und mit den Ergebnissen aus den Experimenten (z.B. dem Spektrum der Wasserstoffentladungslampe) vergleichen kann. | |||
Die Physiker sagen dann auch: Die Wellenfunktion bricht zusammen. | |||
Man kann es sich auch so klarmachen: Die Multiplikation der Wellenfunktion mit sich selbst beschreibt die Zerstörung des Quantensystems und den Übergang in ein anderes, und nur aus den Spuren der Zerstörung kann Erkenntnis über die Natur des vorher bestehenden und nachher entstandenen Systems gewonnen werden. | |||
Vergleiche noch mal mit der Situation der Riesen, die ihre Atome, unsere Autos, ja auch nur erkennen können, indem sie sie zerstören. | |||
|Lösung}} | |||
==Quantenphysikalische Begriffe und fragwürdige Aussagen dazu== | |||
Im Umgang mit der Quantenphysik kann man drei Ebenen unterscheiden: | |||
#Die erste Ebene brachte der Physiker David Mermin 1989 so auf den Punkt: ''Shut up and calculate!'' - Halt den Mund! Rechne! <ref>https://www.spektrum.de/kolumne/quantenphysik-ist-metaphysik-mit-physikalischen-mitteln/1703806</ref> In dieser Perspektive geht es darum, die Ergebnisse von Messungen durch Berechnung als Element der Theorie zu bestätigen, ohne sich über die Natur der Sache, die man da misst, in irgendeiner Weise Gedanken zu machen. Dazu zähle ich auch die Möglichkeiten, die Ergebnisse der Berechnungen und Messungen anschaulich zu präsentieren, wie es in den vorhergehenden Kapiteln versucht wurde. | |||
#Die zweite Ebene ist der Versuch der Physiker, die Objekte der Quantenphysik, meistens ausgehend von den Selbstverständlichkeiten der klassischen Physik, in irgendeiner Form in Begriffe zu fassen. Wenn oben von ''Wellenfunktion'', ''Aufenthaltswahrscheinlichkeit'' usw. gesprochen wurde, waren das schon Beispiele dieser Physik-internen '''Interpretation''', die über das bloße Berechnen und Messen hinausgehen. Weitere Begriffe gliedern in diesem Kapitel die Auseinandersetzung mit den mehr oder weniger zwingenden Folgerungen, die aus der Quantenphysik gezogen worden sind. | |||
#Die dritte Ebene der Interpretation möchte etwas darüber aussagen, was die Einführung der Quantenphysik für das Verhältnis des Menschen zur Natur, zur Welt, zu sich selbst, zur Wissenschaft und zur Religion bedeuten könnte. Es sind wissenschaftstheoretische, naturphilosophische und esotherische Perspektiven, ohne dass die Abgrenzung besonders scharf wäre. Wir ordnen die Auseinandersetzung mit solchen Aussagen unten denjenigen Begriffen zu, an denen sie sich am leichtesten aufhängen lassen. | |||
===Unschärfe=== | |||
Eine Messung kann nicht bestimmter sein, als der Gegenstand, den sie bestimmt. Die Warnung erinnert an Studenten, die drei Messwerte auf zwei Stellen hinter dem Komma gemessen haben, dann multiplizieren und glauben, das Resultat wäre auf sechs Nachkommastellen genau. | |||
{{Box|Grundsatz| | |||
Die Grenze der Bestimmbarkeit in der Natur ist das Plancksche Wirkungsquantum. | |||
Dieses beträgt 6,626 * 10<sup>-34</sup> Joule * Sekunde. | |||
|Merksatz}} | |||
Das Wirkungsquantum, das von {{wpde|Max Planck}} (1858-1947) am 14. Dezember 1900 eingeführt wurde,<ref>Wer Max Planck etwas näher kennen lernen will, dem sein das folgende Video (44 MIN) empfohlen: https://www.youtube.com/watch?v=H0oKzF7bh3I</ref> weshalb dieser Tag als Geburtstag der Quantenphysik gilt, beschreibt zunächst den Zusammenhang zwischen Frequenz (ny) und Energie (E) eines Photon: | |||
<blockquote>E = h * ny</blockquote> | |||
Das seinerzeit Verstörende an dieser Formel ist die Aussage, dass das Licht die Energie in "Paketen" transportiert. Zehn Jahre später entdeckte {{wpde|Robert Millikan}} (1868-1953) die Elementarladung.<ref>Erklärung seines Öltröpfchenexperimentes: https://www.youtube.com/watch?v=P1jMNiiOUW8 (Video 5 MIN)</ref> Das war die zweite Entdeckung einer "gequantelten" Messgröße. Die Bedeutung des Wirkungsquantums als Naturkonstante, die in allen atomaren Vorgängen eine Rolle spielt, hat sich erst nach und nach herausgestellt. | |||
{{wpde|Werner Heisenberg}} hat die {{wpde|Unschärferelation}} formuliert, die zum Ausdruck bringt, dass Messgrößen, deren Produkt eine Wirkung ist, nicht genauer bestimmt werden können als es dem Wirkungsquantum entspricht. Zwei Größen, deren Produkt eine Wirkung ist, sind zum Beispiel "Energie und Zeit", "Impuls und Ort". Heisenberg sprach von "komplementären Messgrößen", und sein Prinzip sagt aus, dass es keine Messmethode geben kann, die beide komplementären Messgrößen unendlich exakt bestimmt. Da das Wirkungsquantum eine so winzig kleine Größe hat, spielt das Unschärfeprinzip bei alltäglichen Messungen keine Rolle; irritierend für diejenigen, die von der klassischen Physik her kommen, ist allerdings die Tatsache, dass es nicht nur eine praktische, sondern auch eine prinzipielle Grenze der Messgenauigkeit gibt. | |||
{{Box|Zitat| | |||
Boff / Hathaway behaupten in ihrem preisgekrönten Werk ''Befreite Schöpfung'': | |||
''Ein .. Merkmal des Quantenmikrokosmos ist der Zufallscharakter oder die Unbestimmtheit. .. Die Welt des linearen Determinismus löst sich mit dieser neuen Wirklichkeit tatsächlich auf, jedenfalls auf subatomarer Ebene.'' <ref>Leonardo Boff/Mark Hathaway: ''Befreite Schöpfung'' aus dem Englischen von Bruno Kern, Kaevelaer 2016, ''113'' Gerhard Kruip weist in seiner Laudatio an Leonardo Boff zur Verleihung der Carl-Friedrich-von-Weizäcker Medaille 2016 ausdrücklich auf das Buch hin: https://www.cfvw.org/files/cfvw/pdf/laudatio_boff-gs.pdf</ref> | |||
|Zitat}} | |||
{{wpde|Determinismus}} bezeichnet die Vorstellung, dass jetzt schon fest steht, was in Zukunft geschieht. Bei {{wpde|Johannes Calvin}} (1509-1564) war es eine logische Folgerung aus der Allmacht und Allwissenheit Gottes, dass die Bestimmung des Menschen zu Heil oder Unheil schon immer in Gottes Ratschluss beschlossen sei und der Mensch selbst nur noch nach Anzeichen der Vorhersehung forschen konnte. Die Physik des 19. Jahrhunderts pflegte den Glauben, der auf {{wpde|Robert Boyle}} (1627-1692) zurückgeht, dass man nur einen Zustand der Welt exakt erfassen müsse, um alle Zustände zuvor und danach nach mathematischen Gesetzmäßigkeiten daraus ableiten zu können wie bei einem perfekten Uhrwerk. | |||
Die praktische Durchführung dieser Zurück- und Vorausberechnung scheitert an einer Reihe prinzipieller Hürden: Wie will man neben jedes "Atom" ein Messgerät stellen, und aus was sollen die Messgeräte denn bestehen? Wie kann man relle Zahlen, die dadurch definiert sind, dass sie unendlich viele unregelmäßig auftretende Stellen hinter dem Komma haben, je exakt bestimmen? | |||
Und es ist ja nicht so, dass die Quantenphysik mit geringerer Messgenauigkeit arbeitet als die Physik des neunzehnten Jahrhunderts, im Gegenteil: Die genauesten Messungen, die Menschen heute durchführen, sind ohne die Nutzung von Quantenphänomenen nicht denkbar. Zum Beispiel setzt das Globale Positionierungssystem {{wpde|GPS}}, mithilfe dessen jedes Smartphone "weiß", wo es sich gerade befindet, eine extrem genaue Messung der Zeit voraus, die nur mit Atomuhren realisiert werden kann. | |||
Es ist also nicht so, dass Vorhersagefähigkeiten, die die Menschen einmal besessen hätten, jetzt verschwunden wären. Richtig ist, dass eine Physik, die auf "Atome" und das Universum insgesamt anzuwenden zu Widersprüchen führt, durch Theorien ersetzt worden ist, die bislang widerspruchsfrei alle Experimente mit den kleinsten Bestandteilen der Materie erklären können, dafür aber den Nachteil der Unanschaulichkeit in Kauf nehmen. Das heißt: Es werden mathematisch Objekte definiert, die prinzipiell nicht in unserer Wahrnehmungswelt vorkommen können und sich nur durch Spuren in der Wahrnehmung verraten. | |||
===Verschränkung=== | |||
Ein Vorurteil sagt, dass Quantenphysik vor allem mit dem ganz Kleinen zu tun hat. "Klein" ist aber vor allem das Plancksche Wirkungsquantum. Um von einem Quantensystem sprechen zu können, muss man die Bestandteile davor schützen, durch Einwirkungen größer oder gleich dem Wirkungsquantum gestört zu werden. Unter dieser Voraussetzung können ungestörte Quantensysteme sehr groß werden, wie Anton Zeilinger durch seine Experimente mit polarisiertem Licht gezeigt hat.<ref>Eine Video zeigt die Experimente zur Quantenteleportation, die Anton Zeilinger mit seinen Studenten in Wien durchgeführt hat: https://www.youtube.com/watch?v=MgM4-4_Dr1w</ref> | |||
{{wpde|Supraleitung}} bedeutet, dass Strom ohne Widerstand fließt, weil die Ladungsträger durch extreme Kühlung in einem kohärenten Quantenzustand sind. Schaut man sich die supraleitenden Magnete am LHC in Genf an,<ref>in diesem Spektrum-Artikel ist ein Foto enthalten: https://www.spektrum.de/news/was-kommt-nach-dem-lhc/1733950</ref> dann sieht man, dass kohärente Systeme sehr groß sein können. | |||
Es kommt also nicht auf die Größe in Zentimetern an, sondern auf die Kohärenz, die Ungestörtheit des Quantensystems. | |||
{{Box|Zitat| | |||
Boff und Hathaway sagen: | |||
Das ''Phänomen, das man .. Quanten-Verschränkung nennt, tritt immer dann auf, wenn zwei Teilchen miteinander in Wechselwirkung treten. Von diesem Augenblick an bleiben sie für immer auf geheimnisvolle Weise miteinander verbunden. .. Das Phänomen der Verschränktheit'' verweist ''auf eine tiefe grundlegende Einheit, die den gesamten Kosmos auf Quantenebene verbindet.''<ref>Boff/Hathaway ''Befreite Schöpfung'', ''126''</ref> | |||
|Zitat}} | |||
"Auf geheimnisvolle Weise miteinander verbunden" bleiben verschränkte Teilchen natürlich nur so lange, wie sie nicht gestört werden. Jede Art von Wechselwirkung zerstört die Verschränkung. Das bedeutet auch, dass man die Verschränkung nicht zur Informationsübertragung nutzen kann. Die "grundlegende Einheit des gesamten Kosmos auf Quantenebene" mag eine inspirierende Vorstellung sein, Ergebnis eines denkbaren Experimentes ist sie nicht. Die Quantenphysik ist keine spirituelle Unternehmung. | |||
Das hindert die Physiker nicht daran, mit der Verschränkung zu experimentieren. Vielleicht werden diese Experimente einmal technische Anwendungen in der Quantenkryptografie, die eine absolut sichere Verschlüsselung von Daten verspricht, oder dem Quantencomputer finden. {{wpde|Anton Zeilinger}} (*1945) hat eine Vorlesung über seine bahnbrechenden Experimente und ihre möglichen technischen Anwendungen gehalten.<ref>Anton Zeilinger: ''Die zweite Quantenrevolution'' (Audiodatei mit Standbild 30 MIN): https://www.youtube.com/watch?v=RwOZGTFkDtY</ref> | |||
===Tunneln=== | |||
===Superposition=== | |||
<references /> | |||
Aktuelle Version vom 5. September 2022, 20:52 Uhr
Einleitung
Aussagen über quantenphysikalische Objekte werden mithilfe sehr komplizierter mathematischer Modelle getroffen, die weit über den Schulunterricht hinausgehen. Aber das gilt auch für die "klassischen" Forschungsbereiche der Physik, z.B. die Hamiltonschen Bewegungsgleichungen![]() oder die Navier-Stokes-Gleichungen
oder die Navier-Stokes-Gleichungen![]() , mit denen die Bewegungen von Gasen und Flüssigkeiten beschrieben werden. Im einen wie im anderen Fall kann man sich aber mit grafischen Darstellungen helfen, die von den Betrachtern intuitiv erfasst werden.
, mit denen die Bewegungen von Gasen und Flüssigkeiten beschrieben werden. Im einen wie im anderen Fall kann man sich aber mit grafischen Darstellungen helfen, die von den Betrachtern intuitiv erfasst werden.
Die Quantenphysik überrascht mit Begriffen, die aus der Perspektive der klassischen Physik sehr fremdartig wirken, z.B. Verschränkung![]() , Tunneln
, Tunneln![]() und Unschärferelation
und Unschärferelation![]() . Man liest, mit der Quantenphysik sei der Zufall in die Physik eingebrochen, und sehr bekannt ist Albert Einsteins
. Man liest, mit der Quantenphysik sei der Zufall in die Physik eingebrochen, und sehr bekannt ist Albert Einsteins![]() Widerstand gegen die Quantenphysik und seine zumeist verkürzt zitierte Formulierung: Gott würfelt nicht.[1] Aber den Zufall kann auch die klassische Physik nicht vertreiben, denn in ihr sind physikalische Messwerte als reelle Zahlen
Widerstand gegen die Quantenphysik und seine zumeist verkürzt zitierte Formulierung: Gott würfelt nicht.[1] Aber den Zufall kann auch die klassische Physik nicht vertreiben, denn in ihr sind physikalische Messwerte als reelle Zahlen![]() definiert; das sind Zahlen mit unendlich vielen regellos auftretenden Stellen hinter dem Komma, die niemals wirklich genau erfasst werden können. Das hat zur Folge, dass Voraussagen - beispielsweise über das Wetter
definiert; das sind Zahlen mit unendlich vielen regellos auftretenden Stellen hinter dem Komma, die niemals wirklich genau erfasst werden können. Das hat zur Folge, dass Voraussagen - beispielsweise über das Wetter![]() - immer nur für eine begrenzte Zukunft zuverlässig sein können, denn irgendwann werden die feinen Unterschiede, die man nicht hat messen können, für die weitere Entwicklung ausschlaggebend sein.[2]
- immer nur für eine begrenzte Zukunft zuverlässig sein können, denn irgendwann werden die feinen Unterschiede, die man nicht hat messen können, für die weitere Entwicklung ausschlaggebend sein.[2]
Dieser Lernpfad zur Quantenphysik möchte zweierlei vermeiden:
- Es geht nicht darum, Mathematische Methoden zu vermitteln, die man sich mit der Schulmathematik nicht erarbeiten kann. Für Physikstudenten steht ja eine reiche Auswahl an Lehrbüchern bereit.[3]
- Es ist mir zu wenig, nur die Phänomene zu benennen ohne die logischen Konzepte, die ihrer mathematischen Beschreibung zugrundliegen. Wer diese nicht berechnen kann, kann doch wenigstens ihre grafische Veranschaulichung erfassen und so ein gewisses Verständnis erzielen. Dazu braucht man einen Einstieg, und den habe ich gewählt bei der Frage: Was ist eine Messung? Denn das unterscheidet seit Galileo Galileis
 Zeiten Physik von alltäglichem Hinschauen: Die zahlenmäßige Erfassung eines Ausschnittes der Wirklichkeit mit dem Ziel der Berechnung der Zusammenhänge.
Zeiten Physik von alltäglichem Hinschauen: Die zahlenmäßige Erfassung eines Ausschnittes der Wirklichkeit mit dem Ziel der Berechnung der Zusammenhänge.
Eine Messung
Vor einiger Zeit – ich bin nicht stolz darauf - bekam ich von der Stadt Grünberg einen Brief, aus dem ich einen Ausschnitt zeige:
Über die Messung, die in diesem Fall durchgeführt worden ist, stehen im Bescheid einige für unser Thema relevante Informationen:
- Es sind Laserstrahlen hergestellt worden, deren spezifische Eigenschaft, Kohärenz
 , nur mit Mitteln der Quantenphysik verstanden werden kann. Und das kann man verallgemeinern: Gleichgültig ob wir mit Hilfe von Licht etwas "sehen", mithilfe chemischer Prozesse etwas "schmecken" oder "riechen" oder ob wir mechanische Reizungen "fühlen" oder "hören" - immer ist die Quantenphysik im Spiel.
, nur mit Mitteln der Quantenphysik verstanden werden kann. Und das kann man verallgemeinern: Gleichgültig ob wir mit Hilfe von Licht etwas "sehen", mithilfe chemischer Prozesse etwas "schmecken" oder "riechen" oder ob wir mechanische Reizungen "fühlen" oder "hören" - immer ist die Quantenphysik im Spiel. - Eine klassische Messgröße, die Geschwindigkeit eines Fahrzeugs, konnte zu einem bestimmten Zeitpunkt an einem bestimmten Ort mit so großer Genauigkeit festgestellt und der Person des Autofahrers zugeordnet werden, dass mir kein Gericht Recht geben wird, wenn ich meine Ordnungswidrigkeit leugnen wollte. Deshalb wird es am einfachsten und risikoärmsten sein, den Bußgeldbescheid zu bezahlen.
- Benenne ein anderes Beispiel einer Messung
- Beschreibe möglichst exakt, was derjenige tut, der die Messung durchführt.
- Versuche, die quantenphysikalischen Objekte zu benennen, die in dem Messvorgang beteiligt sind (z.B. Licht, Chemie)
- Gib an, welche Konsequenzen die Messung hat, wie genau sie dazu sein muss und welche Folgen Fehler haben können.
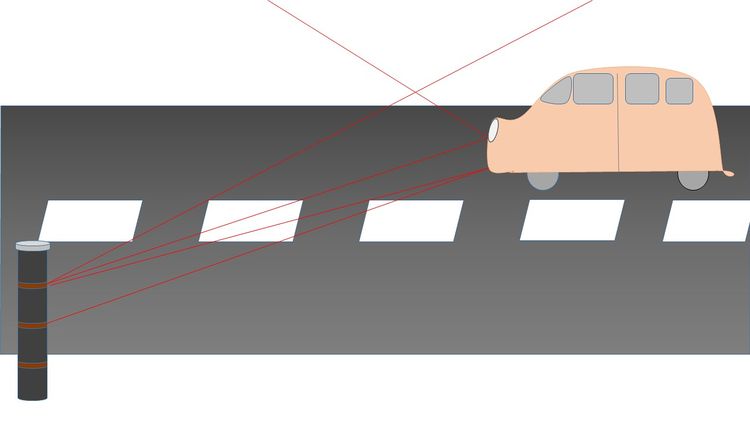
Wir machen uns klar, was bei der Geschwindigkeitsmessung mit einem Lasergerät![]() passiert:
passiert:
- Das Messgerät beschießt das fahrende Auto mit Lichtteilchen, von denen einige so reflektiert werden, dass sie zum Messgerät zurückkehren, welches automatisch die Geschwindigkeit bestimmt.
- Das Auto wird fotografiert und anhand des Nummernschildes identifiziert, sodass der Strafzettel den richtigen Autobesitzer erreicht, und das Foto ermöglicht die Identifikation des Fahrers.
- Weil masselose Lichtteilchen, verglichen mit einem tonnenschweren Auto, sehr wenig Energie transportieren, kann man im Falle einer Verkehrskontrolle davon ausgehen, dass die Messmethode die gemessene Geschwindigkeit nicht beeinflusst und weder das Nummerschild noch das Portraitfoto manipuliert.
Was ändert sich, wenn das Beobachtungsobjekt kein tonnenschweres Auto ist, sondern eines des leichtesten, kleinsten, flüchtigsten Teilchen der Natur?
Das Atom
Empedokles![]() aus Agrigent (495-435 v.C.) hatte den Philosophenstreit, ob alle Dinge nun aus dem Wasser, dem Feuer oder dem Hauch entstanden seien, dadurch beendet, dass er alle vier Elemente - Erde, Wasser, Feuer und Luft (heute sprechen wir von Aggregatzuständen
aus Agrigent (495-435 v.C.) hatte den Philosophenstreit, ob alle Dinge nun aus dem Wasser, dem Feuer oder dem Hauch entstanden seien, dadurch beendet, dass er alle vier Elemente - Erde, Wasser, Feuer und Luft (heute sprechen wir von Aggregatzuständen![]() ) - zu Grundbestandteilen allen Daseins erklärt hatte.
) - zu Grundbestandteilen allen Daseins erklärt hatte.
Demokrit![]() von Abdera (460-370) baute auf diesen Überlegungen auf und postulierte, die vier Elemente müssten aus unteilbaren Teilchen bestehen, die er atomoi nannte, zu deutsch: Unteilbare <Teilchen>. Er stellte sich diese Atome als winzig kleine geometrisch sehr regelmäßige "Bauklötzchen" vor: Kugeln, Würfel, Zylinder, Kegel, die sich im vollkommen leeren Raum bewegen. Später hat man die fünf regelmäßigen platonischen Körper
von Abdera (460-370) baute auf diesen Überlegungen auf und postulierte, die vier Elemente müssten aus unteilbaren Teilchen bestehen, die er atomoi nannte, zu deutsch: Unteilbare <Teilchen>. Er stellte sich diese Atome als winzig kleine geometrisch sehr regelmäßige "Bauklötzchen" vor: Kugeln, Würfel, Zylinder, Kegel, die sich im vollkommen leeren Raum bewegen. Später hat man die fünf regelmäßigen platonischen Körper![]() den Elementen zugeordnet: der Erde den Würfel, dem Wasser den Ikosaeder, der Luft den Oktaeder und dem Feuer die Pyramide. Der Dodekaeder sollte die Himmelsmaterie bilden, die fünfte essentia, von deren Natur wir nichts wissen.
den Elementen zugeordnet: der Erde den Würfel, dem Wasser den Ikosaeder, der Luft den Oktaeder und dem Feuer die Pyramide. Der Dodekaeder sollte die Himmelsmaterie bilden, die fünfte essentia, von deren Natur wir nichts wissen.
Schon Aristoteles![]() aus Stagira (399-322) kritisierte die Atomtheorie, weil er Bewegung in einem vollkommen leeren Raum für unmöglich hielt. Auch konnte sich niemand vorstellen, wie die Atome Kontakt miteinander aufnehmen und sich zu größeren Körpern verbinden sollten. Sie können ja keine "Ärmchen" haben, mit denen sich sich "unterhaken".
aus Stagira (399-322) kritisierte die Atomtheorie, weil er Bewegung in einem vollkommen leeren Raum für unmöglich hielt. Auch konnte sich niemand vorstellen, wie die Atome Kontakt miteinander aufnehmen und sich zu größeren Körpern verbinden sollten. Sie können ja keine "Ärmchen" haben, mit denen sich sich "unterhaken".
Denke darüber nach,
- warum die Atomtheorie des Demokrit so verführerisch ist,
- und warum es nicht stimmen kann, dass die Welt aus lauter "Bauklötzchen" besteht, die wir wegen ihrer Kleinheit nie zu sehen bekommen und warum das auch unbefriedigend wäre.
Stell Dir vor, du gehörst zu einer Riesenwelt. Für die Riesen sind Objekte von der Größenordnung von Autos das Kleinste, was sie wahrnehmen können.
- Was können die Riesen tun, um etwas über Autos herauszufinden?
- Was werden sie nie herausbekommen können?
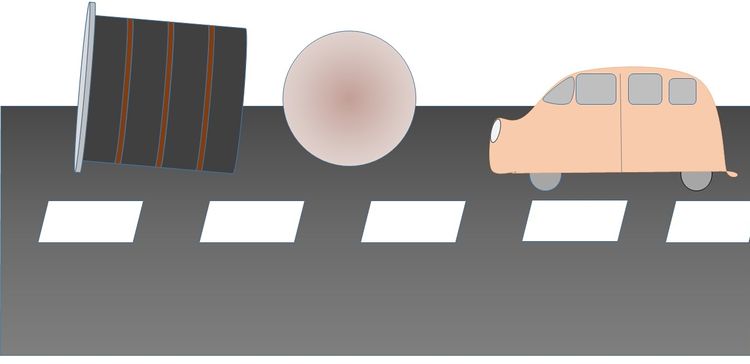
Die Riesen könnten eine aus ihrer Perspektive winzige Kanone herstellen und die Autos damit beschießen. Aus unserer Zwergenperspektive wird nach der Kollision nichts mehr sein, wie es war:
- Kugel und Auto werden sich zu Trümmerteilen verformen.
- Ihre Geschwindigkeiten und Bewegungsrichtungen werden sich stark verändern.
Die Riesen sehen nur punktförmige Objekte, die sich z.B. auf einem Fotosensor bemerkbar machen. Wenn sie das Experiment mit verschiedenen Parametern durchführen, können sie sicher etwas über die Masse und die Geschwindigkeit der beteiligten Objekte sagen und den Ort der Kollision bestimmen.
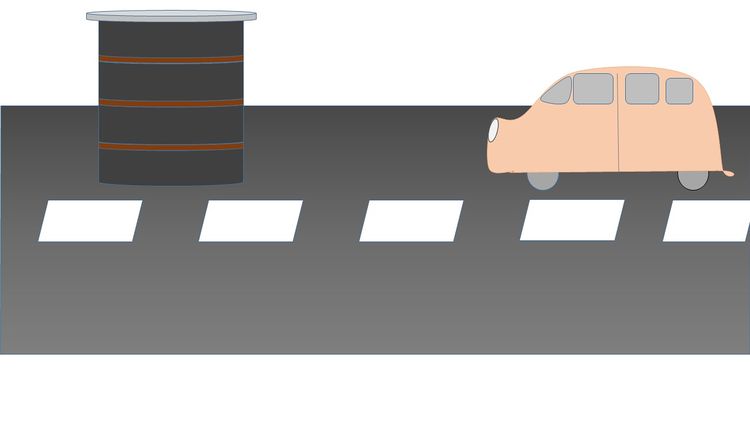
Die Riesen könnten das Verhalten von Autos auch an fest montierten Objekten studieren und feststellen, dass die Objekte vor dem Objekt stehen bleiben oder es mit reduzierter Geschwindigkeit passieren. Welchen Reim werden sie sich darauf machen?
Diese Riesen werden niemals Bußgeldbescheide verschicken.
- Da für sie Autos unteilbar sind, können sie in und an ihnen weder Fahrer noch Nummernschild sehen und das einzelne Auto nicht identifizieren und nachverfolgen.
- Wem sollten sie Bußgeldbescheid schicken, denn das Auto ist nach der Kollision kaputt, und der Fahrer wird nicht mehr in der Lage sein, Strafe zu zahlen.
Wasserstoff
Die "Kanonenkugeln" der Quantenphysiker sind Photonen, übersetzt etwa Lichtteilchen. Photonen![]() übermitteln nicht nur das Licht, sondern auch Wärme und Radiosignale, Röntgen- und Gammastrahlen. Zwei unserer fünf Sinne, Tastsinn und Gehör, verarbeiten mechanische Signale. Damit eine Wahrnehmung zustandekommt, müssen die Schallwellen und Texturen zuerst in chemische und elektrische Signale verwandelt werden, und dabei spielen wieder die Photonen eine Rolle. Der Gesichtssinn wandelt Photonen durch die Netzhaut direkt in Signale um, die das Nervensystem verarbeiten kann; Geruch und Geschmack verarbeiten chemische Eigenschaften der Stoffe, die von der Nasenschleimhaut oder der Zunge durch Photonenaustausch erfasst werden.
übermitteln nicht nur das Licht, sondern auch Wärme und Radiosignale, Röntgen- und Gammastrahlen. Zwei unserer fünf Sinne, Tastsinn und Gehör, verarbeiten mechanische Signale. Damit eine Wahrnehmung zustandekommt, müssen die Schallwellen und Texturen zuerst in chemische und elektrische Signale verwandelt werden, und dabei spielen wieder die Photonen eine Rolle. Der Gesichtssinn wandelt Photonen durch die Netzhaut direkt in Signale um, die das Nervensystem verarbeiten kann; Geruch und Geschmack verarbeiten chemische Eigenschaften der Stoffe, die von der Nasenschleimhaut oder der Zunge durch Photonenaustausch erfasst werden.
Aber wir sehen und riechen mithilfe der Photonen. Wir nehmen die Lichtteilchen selbst nicht wahr, und wir reden über die wahrgenommenen Objekte, nicht über die Mechanismen der Wahrnehmung. Wir sagen: Die Rose ist rot oder Die Suppe ist zu salzig, ohne uns Gedanken darüber zu machen, auf wie komplizierten Wegen die Information über die Objekte zu uns gekommen ist.
Diese Ignoranz können sich Atomforscher nicht leisten. Sie benötigen eine Theorie des Lichtes, um ermitteln zu können, was sie mithilfe des Lichtes in der atomaren Welt „sehen“.
Zwei Elemente der Licht-Theorie werden unten vorausgesetzt:
- Jedes Lichtteilchen transportiert Energie
 .
. - Die Energie ist proportional zu seiner Frequenz
 und umgekehrt proportional zur Wellenlänge
und umgekehrt proportional zur Wellenlänge .
.
Das „Haustier“ der Quantenphysiker ist der Wasserstoff![]() . Antoine Laurent de Lavoisier
. Antoine Laurent de Lavoisier![]() (1743-1794) hat dem Gas seinen Namen gegeben. Dmitri Iwanowitsch Mendelejew
(1743-1794) hat dem Gas seinen Namen gegeben. Dmitri Iwanowitsch Mendelejew![]() (1834-1907) wies ihm einen Platz in seinem Periodensystem
(1834-1907) wies ihm einen Platz in seinem Periodensystem![]() zu: Ein reaktionsfreudiges Element mit dem leichtesten Atomgewicht von allen und der Ordnungszahl 1, weil nur ein Proton seinen Atomkern bildet.
zu: Ein reaktionsfreudiges Element mit dem leichtesten Atomgewicht von allen und der Ordnungszahl 1, weil nur ein Proton seinen Atomkern bildet.
Da man dem Wasserstoffatom einen elektrisch negativ geladenen Bestandteil klauen kann, stellen wir es uns vor als "Zusammensetzung" aus einem positiv geladenen Teil – Proton![]() genannt – und aus einem negativ geladenen – dem Elektron
genannt – und aus einem negativ geladenen – dem Elektron![]() . Solche Wörter aus der Alltagssprache gehören in der Quantenphysik in Anführungszeichen, denn wenn ein Objekt unserer Alltagswelt aus mehreren kleineren "zusammengesetzt" ist, dann sind wir daran gewöhnt, das Objekt mit Schere, Messer, Schrauber oder Stemmeisen "zerlegen" zu können. Auch das Wasserstoffatom kann "zerlegt" werden, aber nicht, indem man ein Instrument "zwischen" Elektron und Proton bringt, sondern nur, indem man das Elektron "lockt".
. Solche Wörter aus der Alltagssprache gehören in der Quantenphysik in Anführungszeichen, denn wenn ein Objekt unserer Alltagswelt aus mehreren kleineren "zusammengesetzt" ist, dann sind wir daran gewöhnt, das Objekt mit Schere, Messer, Schrauber oder Stemmeisen "zerlegen" zu können. Auch das Wasserstoffatom kann "zerlegt" werden, aber nicht, indem man ein Instrument "zwischen" Elektron und Proton bringt, sondern nur, indem man das Elektron "lockt".
Wie sich Proton und Elektron im Wasserstoffatom verhalten, konnte die Quantenphysik aufklären, und das gehört zu ihren brillantesten Leistungen. Im Folgenden werden einige Aspekte der Theorie qualitativ dargestellt. Die mathematischen Rechenvorschriften der Theorie können im Bild veranschaulicht werden. Aus solchen Abbildungen geht zwar nicht hervor, wie die Physiker darauf gekommen sind, aber man kann damit schon erläutern, was sie meinen.
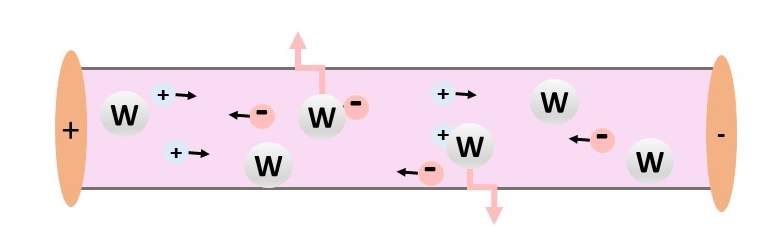
Um Wasserstoff besser kennen zu lernen, wird etwas Gas isoliert, in ein Röhrchen eingeschlossen und von beiden Seiten unter Strom gesetzt.
Was, glaubst Du, wird geschehen?
Wenn Druck und Spannung stimmen, wird das Gas blau-violett leuchten. Warum?
Wasserstoff besteht aus Ladungsträgern, positiv geladenen Protonen und negativ geladenen Elektronen. Wenn der Strom fließt, werden geladene Partikel vom gegensätzlich geladenen Pol angezogen und sich dahin auf den Weg machen. Es wird zu Rempeleien mit den Wasserstoffatomen kommen, die Elektronen werden entweder ganz aus dem Atom geschlagen oder auf eine andere Bahn um das Proton geworfen. Da bewegte geladene Partikel elektromagnetische Strahlung aussenden, erklärt sich so das Licht.
"Licht![]() " nennen wir den Teil elektromagnetischer Strahlung, den wir sehen können. Denn die Lichtteilchen, die die elektromagnetische Strahlung transportieren, unterscheiden sich darin, wieviel Energie sie mitbringen, die - wir erinnern uns - mit der Frequenz und der Wellenlänge zusammenhängt.
" nennen wir den Teil elektromagnetischer Strahlung, den wir sehen können. Denn die Lichtteilchen, die die elektromagnetische Strahlung transportieren, unterscheiden sich darin, wieviel Energie sie mitbringen, die - wir erinnern uns - mit der Frequenz und der Wellenlänge zusammenhängt.
Licht ändert beim Übergang von Luft in Glas oder Wasser seine Richtung ein wenig; man sagt, es wird gebrochen. Lässt man Licht durch ein Prisma![]() fallen, werden nicht alle Farben (mitdenken: Frequenzen, Wellenlängen) um den gleichen Winkel umgelenkt, sondern das Licht spaltet sich auf in seine Spektralfarben. Das Spektrum
fallen, werden nicht alle Farben (mitdenken: Frequenzen, Wellenlängen) um den gleichen Winkel umgelenkt, sondern das Licht spaltet sich auf in seine Spektralfarben. Das Spektrum![]() einer Glühlampe oder der Sonne sieht dann so aus wie das Bild oben, das uns als Himmelserscheinung vertraut ist: der Regenbogen
einer Glühlampe oder der Sonne sieht dann so aus wie das Bild oben, das uns als Himmelserscheinung vertraut ist: der Regenbogen![]() .
.
Das Licht, das wir sehen können, hat eine Frequenz von höchstens 780 Terahertz; das entspricht einer Wellenlänge von 380 Nanometern und der Farbe blauviolett links, und es hat eine Frequenz von mindestens 785 Terahertz und eine Wellenlänge von 780 Nanometern; das ist das purpurrote Licht rechts. Dazwischen liegen alle anderen Farben in einer bestimmten Reihenfolge: Man spricht vom Farbenspektrum.
Kommen wir zurück zur Wasserstoff-Entladungslampe.
Man kann das Licht der Wasserstofflampe durch ein Prisma aufspalten, wie wird das aussehen?
Wenn wir an die Rempelei zwischen den verschiedenen Ladungsträgern in dem Gas zurückdenken, dann müssten die erzeugten Photonen alle möglichen Energiebeträge mitnehmen: Manche Atome werden mittig getroffen; da knallts heftig, andere werden nur in einem mehr oder weniger flachen Winkel gestreift; da entsteht wenig Lichtenergie. Wir erwarten also ein kontinuierliches Farbenspektrum, vielleicht in dem Wellenlängenbereich ein wenig schmäler als das weiße Sonnenlicht; so könnte man die Farbigkeit der Wasserstofflampe erklären.
Was tatsächlich passiert ist etwas völlig anderes: Das Spektrum des Wasserstoffes besteht aus scharfen Linien und die dazwischenliegenden Farben kommen nicht vor.
Schon 1888 formulierte der schwedische Physiker Janne Rydberg![]() eine Formel, aus der man die Linien ableiten kann. Aber damit war natürlich noch nicht erklärt, warum das Wasserstoffspektrum nicht kontinuierlich ist, sondern aus Linien besteht, die eine mathematisch ableitbare Regelmäßigkeit besitzen.
eine Formel, aus der man die Linien ableiten kann. Aber damit war natürlich noch nicht erklärt, warum das Wasserstoffspektrum nicht kontinuierlich ist, sondern aus Linien besteht, die eine mathematisch ableitbare Regelmäßigkeit besitzen.
Quantenphysikalische Zustände
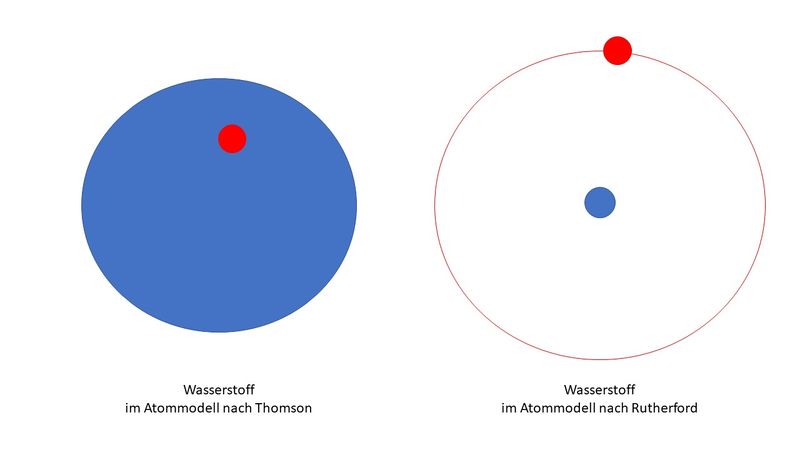
Joseph John Thomson![]() stellte sich 1903 das Atom nach Art eines Rosinenkuchens vor: Die Elektronen sollten sich im Proton aufhalten wie Rosinen in einem Rosinenkuchen, im Wasserstoffatom eine einzige Rosine, im Goldatom 79 Stück.
stellte sich 1903 das Atom nach Art eines Rosinenkuchens vor: Die Elektronen sollten sich im Proton aufhalten wie Rosinen in einem Rosinenkuchen, im Wasserstoffatom eine einzige Rosine, im Goldatom 79 Stück.
Ernest Rutherford![]() argumentierte, dass es dann nur eine Spektrallinie geben dürfte. Er konstruierte 1911 ein planetarisches Atommodell, nach dem sich die Elektronen um den Atomkern bewegen wie Planeten um ihre Sonne.
argumentierte, dass es dann nur eine Spektrallinie geben dürfte. Er konstruierte 1911 ein planetarisches Atommodell, nach dem sich die Elektronen um den Atomkern bewegen wie Planeten um ihre Sonne.
Die Physiker mussten sich also im ersten Viertel des 20. Jahrhunderts etwas vollkommen Neues überlegen. Dabei mussten sie eine Voraussetzung aufgeben, die bis dahin selbstverständlich hingenommen worden war, nämlich, dass alle physikalischen Objekte anschaulich sind.
Unsere gesamte Wahrnehmung und unsere Handlungsmöglichkeit beruhen darauf,
- dass wir uns in einer Zeit befinden, die von gestern nach morgen, von eben noch bis jetzt gleich dahinfließt,
- dass wir uns in einem Raum bewegen, in dem sich vorne und hinten, oben und unten, rechts und links voneinander unterscheiden lassen.
- Zeit und Raum können wir durch Koordinatensysteme abbilden und allem, was sich darin befindet, durch reelle Zahlen einen Ort zuweisen. (Wir wissen, dass wir die reellen Zahlen nicht vollkommen genau messen können; aber für die praktischen Erfordernisse messen wir genau genug, um zum Beispiel einen Satelliten sicher zum Mond zu bringen und wieder zurück.
Die Anschaulichkeit ist Bedingung der Möglichkeit von Erfahrung und Handeln, wie Immanuel Kant![]() in seiner Kritik der reinen Vernunft 1781 nachgewiesen hat. Allerdings sind weder die Welt insgesamt, noch ihre kleinsten Teilchen in einem anschaulichen Modell widerspruchsfrei zu beschreiben; das hat Kant auch bewiesen.
in seiner Kritik der reinen Vernunft 1781 nachgewiesen hat. Allerdings sind weder die Welt insgesamt, noch ihre kleinsten Teilchen in einem anschaulichen Modell widerspruchsfrei zu beschreiben; das hat Kant auch bewiesen.
Welle-Teilchen-Dualismus
Die Physik der Neuzeit hat mathematische Methoden entwickelt, um die verschiedenen Phänomene, die uns umgeben, zahlenmäßig zu erfassen (Messung) und zu berechnen:
- Die Physik des Massenpunktes beschreibt Bewegungen, die man mit hinreichender Genauigkeit als Bewegungen eines punktförmigen Objektes ansehen kann (z.B. der Schwerpunkt einer Kugel). Zu diesem Formalismus gehören Begriffe wie Geschwindigkeit, Beschleunigung, Impuls, kinetische Energie. An einem bekannten Experiment zur Impulserhaltung, dem Verhalten der Newtonwiege
 soll die Konzeption exemplarisch verdeutlicht werden.
soll die Konzeption exemplarisch verdeutlicht werden.
Die Newtonwiege besteht aus fünf gleich schweren Kugeln, die an gleich langen Fäden aufgehängt sind. Unter einem elastischen Stoß versteht man einen Zusammenstoß, bei dem (fast) keine Bewegungsenergie verloren geht. Dadurch kann bei der Newtonwiege die Impulserhaltung (Impuls gleich Masse mal Geschwindigkeit) besonders gut demonstriert werden. (Ein Kaugummi, an der richtigen Stelle auf eine Kugel geklebt, würde das Experiment völlig verändern.) Schau Dir jetzt die Experimente mit der Newtonwiege an und suche Dir wenigstens zwei davon aus, um die Impulserhaltung zu beschreiben.
- Die Physik der Schwingungen und Wellen beschreibt Erscheinungen, die nur in größeren Ansammlungen von Materie auftreten. Zum Beispiel wird ein ins Wasser geworfener Stein Wellen erzeugen, das sind periodische Veränderungen der Wasserhöhe. Wenn du in eine Blockflöte bläst und Schallwellen erzeugst, entstehen periodische Druckschwankungen. Zur Physik der Schwingungen und Wellen gehören folgende Begriffe:
- Frequenz (Zahl der Wellen pro Zeiteinheit)
- Amplitude (Intensität der Schwingung)
- Resonanz (Mitschwingen eines dazu fähigen Objektes)
- Interferenz (Schwingungmuster, das durch die gegenseitige Beeinflussung zweier Wellen entsteht)
Wer sich den Begriff "Interferenz" detailliert beschreiben lassen will, sieht sich folgendes Video an:
Welle-Teilchen-Dualismus bedeutet nun, dass man zur Beschreibung eines Quantensystems (z.B. ein Elektron im Wasserstoffatom) die beiden Formalismen zur Berechnung eines Teilchens (Massenpunktes) und einer Welle in einem Formalismus zusammenfasst.
Komplexe Zahlen
Die Mathematik hat ihre liebe Not mit den Umkehroperationen.
Solange ich addiere und multipliziere, kann ich sicher sein, dass ich ein gültiges Ergebnis herausbekomme: 5 + 3 = 8 und 5 * 3 = 15. Das ist kinderleicht. Das funktioniert immer, egal, mit welchen beiden natürlichen Zahlen ich diese Operation durchführe. Nun sind wir aber vorwitzig und wollen zum Beispiel auch solche Fragen beantworten: Mit welcher Zahl muss ich 5 multiplizieren, um 15 herauszubekommen? Das ist immer noch einfach 15 / 5 = 3. Aber wenn ich mir diese Aufgabe stellen kann, kann ich auch eine andere Aufgabe hinschreiben: 15 / 0 = ? Gut, aufschreiben kann ich die Aufgabe, aber Sinn hat sie keinen. Wenn ich 15 Orangen habe und unter 3 Leuten aufteilen soll, kriegt jeder fünf. Wenn ich sechs Orangen habe und unter vier Leuten aufteile, muss ich zwei in der Mitte durchschneiden, und jeder bekommt eine ganze und eine halbe. Das hat alles Sinn. Aber wenn ich 15 Orangen habe und niemand da ist, der etwas davon kriegen soll, wie viel kriegt dann keiner? Das macht keinen Sinn. Also sollten wir die Aufgabenstellung "15 / 0" einfach verbieten.
Eine Ebene höher geht es darum, Zahlen einmal oder öfter mit sich selbst zu multiplizieren. Die Umkehrfrage lautet dann zum Beispiel: Welche Zahl muss ich mit sich selbst multiplizieren, um 1 herauszubekommen? - Die Antwort ist leicht zu finden, denn 1 * 1 = 1. Aber diese Antwort ist nicht ausreichend, denn -1 * -1 = 1 gilt (Man erinnert sich Minus mal Minus gibt plus.) ebenfalls. Es gilt also:
Was ist jetzt, wenn wir die Aufgabe niederschreiben: " ?"
Wir können auch diese Aufgabenstellung einfach verbieten. Aber große Mathematiker wie Gerolamo Cardano![]() (1501-1576) und Carl Friedrich Gauß
(1501-1576) und Carl Friedrich Gauß![]() (1777-1855) probierten aus, was passiert, wenn man der Aufgabe eine Lösung zuordnet durch die Definition:
(1777-1855) probierten aus, was passiert, wenn man der Aufgabe eine Lösung zuordnet durch die Definition:
oder andersherum i * i = -1
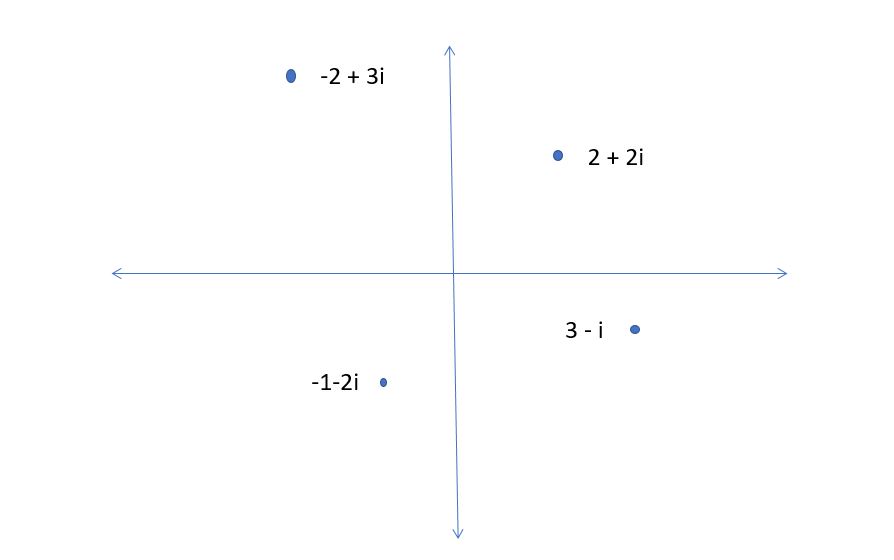
Während eine reelle Zahl als Punkt auf einer Zahlengeraden vorgestellt wird, entsteht jetzt eine Zahlenebene: Eine komplexe Zahl hat also zwei Komponenten: Den gewöhnlichen reellen Anteil und einen imaginären Anteil, eine reelle Zahl, multipliziert mit der imaginären Einheit .
Quantenphysikalische Zustände werden mit komplexen Zahlen beschrieben. Auf diese Weise hat man etwas mehr Platz, die Physik der Wellen und die Physik der Massenpunkte zusammen in den Zustandsgleichungen unterzubringen. Anderseits verzichtet man durch die komplexen Funktionen auf die Anschaulichkeit, denn Messergebnisse im Raum unserer Wahrnehmungen sind reell und nicht komplex.
Kohärenz
Es hat ein bisschen gedauert, aber jetzt sind die Elemente zusammen, die gebraucht werden, um das Spektrum des Wasserstoffs zu interpretieren. Wie sich Elektronen in der Nähe des Atomkerns verhalten, können diejenigen, die sich damit auskennen, aus der Schrödinger-Gleichung![]() ableiten. Die folgende Zeichnung veranschaulicht zwei Lösungen der Gleichung:
ableiten. Die folgende Zeichnung veranschaulicht zwei Lösungen der Gleichung:
Schau Dir die Veranschaulichung in Ruhe an und gib Dir Rechenschaft darüber, was zu sehen ist.
Eigenschaften eines kohärenten Quantensystems
- Das Bild ist nicht etwa ein Foto eines Wasserstoffatoms. Denn ein ungestörtes Atom sendet kein Licht aus und hat keinerlei Wechselwirkung mit seiner Umgebung.
- Mathematisch kommt das darin zum Ausdruck, dass die Funktionswerte komplexe Zahlen sind, Messwerte aber relle Zahlen sein müssen. Diese komplexen Zahlen veranschaulicht die Zeichnung.
- Im Wellenbild des Elektronenzustands kann man die Intensität der Färbung als Amplitude (Auslenkung) der Welle interpretieren.
- Im Teilchenbild entspricht die Farbintensität der Wahrscheinlichkeit, dass sich das Elektron an dieser Stelle aufhält.
- Anders als in Gleichnungen der klassischen Physik kommt in quantenphysikalischen Zustandsgleichungen das Plancksche Wirkungsquantum h = 6,23 * 10 -34 Joule * Sekunde vor. Das ist die kleinste mögliche Wirkung, die ein physikalisches System auf seine Umgebung ausüben kann.
- Ebenfalls neu ist, dass in quantenphysikalischen Gleichungen ganze Zahlen vorkommen, die Quantenzahlen. Die beiden oben abgebildeten Orbitale unterscheiden sich in der Hauptquantenzahl, die den Abstand zum Atomkern bestimmt. Die kleinste Elektronenschale hat die Hauptquantenzahl n=1, die nächstgrößere n=2 usw.
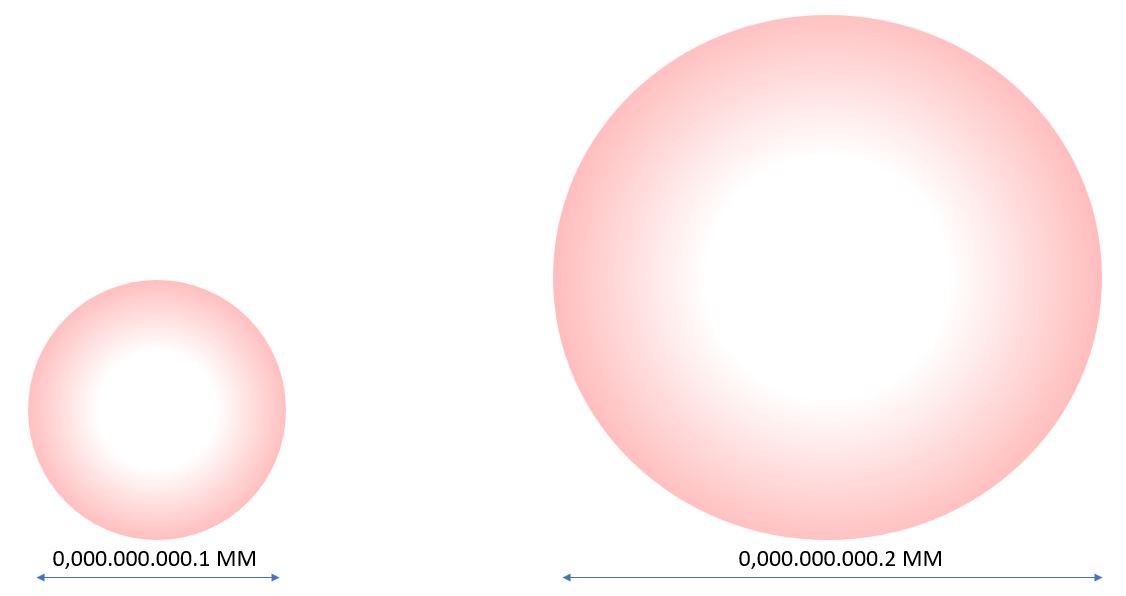
- In der innersten Schale, in der das Elektron sich innerhalb von einem Zehnmilliardstel Millimeter um den Atomkern aufhält, ist nur Platz für ein einziges kugelsymmetrisches Orbital.
- In den größeren Schalen ist mehr Platz. Das drückt sich darin aus, dass die Nebenquantenzahl, die Form und Symmetrieeigenschaften eines Orbitals bezeichnet, höchstens l=n-1 sein kann. Die Magnetquantenzahl wiederum kann m=-l, .. m=0 .. , m=l sein und bezeichnet die Ausrichtung der Symmetrieachse des Orbitals im Raum.
- Unten ist ein hantelförmiges Orbital veranschaulicht, dessen Symmetrieachse von oben nach unten geht, es gibt zwei weitere so geformte Orbitale mit der Symmetrieachse von rechts nach links oder von vorne nach hinten durch die Bildebene. Zusammen mit dem kugelförmigen Orbital wird die zweite Schale also von insgesamt vier Orbitalen ausgefüllt. In der dritten Schale ist logischerweise noch mehr Platz für weitere Orbitalformen.
- Im Wasserstoffatom gibt es nur ein Elektron, das sich in einem der Orbitale befinden kann, je nachdem wie viel Bewegungsenergie es hat. In den größeren Atomen können in jedem Orbital zwei Elektronen Platz finden, die sich im Spin unterscheiden, denn der kann s = + 1/2 oder s = -1/2 betragen.
- Die Pauli-Regel sagt nämlich, dass sich alle Elektronenzustände in einem System in mindestens einer der vier Quantenzahlen n, l, m und / oder s unterscheiden müssen.
- Das Periodensystem
 der chemischem Elemente lässt sich in seinem Aufbau dadurch erklären, dass die Elektronen, deren Zahl die Ordnungszahl
der chemischem Elemente lässt sich in seinem Aufbau dadurch erklären, dass die Elektronen, deren Zahl die Ordnungszahl des jeweiligen Elementes bestimmt, nacheinander die Orbitale auffüllen, die jeweils die geringste Bewegungsenergie besitzen.
des jeweiligen Elementes bestimmt, nacheinander die Orbitale auffüllen, die jeweils die geringste Bewegungsenergie besitzen.
Ein gut zu verstehender Film erläutert das System der Quantenzahlen:
Messung (Störung)
Wie schön und elegant ein physikalisches Modell auch sein mag, Physik wird erst daraus, wenn wir die Objekte des Modells nötigen können, Spuren in unserer Wahrnehmungswelt zu hinterlassen: Ausschläge eines Messgerätes, Spuren auf einem Foto oder eben Spektrallinien.
Bei der Betrachtung der Spektrallinien einer Wasserstoffgasentladung hatten wir uns darüber gewundert, dass es kein regenbogenartiges kontinuierliches Spektrum gibt, sondern diskrete Linien.
Wenn du die Eigenschaften des kohärenten Quantenzustandes eines Elektrons in der Umgebung des Wasserstoffatoms noch einmal durchdenkst, kannst du dann diesen erstaunlichen Befund erklären?
Die Vorstellung, was in dem stromdurchflossenen Glasrohr mit Wassestoffgas passiert, brauchen wir kaum zu korrigieren: Zwischen den zu den elektrischen Polen eilenden Ladungsträgern und den Wasserstoffatomen kommt es zu einer Rempelei, bei der die Elektronen aus der Bahn geworfen werden.
Allerdings können sich die Elektronen nicht frei bewegen, sondern nur in den durch die Quantenzahlen festgelegten Orbitalen (es sei denn, die Bewegungsenergie reicht aus, das Elektron ganz vom Atomkern zu trennen.)
Wenn die Elektronen dann vom Atom eingefangen werden oder von einer äußeren Schale (mit mehr Bewegungsenergie) auf eine weiter innen liegende "herunterfallen", geben sie die Energiedifferenz an ein Lichtteilchen, ein Photon ab.
Einzelheiten:
- Eine violette Linie bei einer Wellenlänge 410,2 nm entsteht, wenn das Elektron vom Atom eingefangen wird und das Orbital n = 2 besetzt.
- Die blauviolette Linie bei der Wellenlänge 431 nm entsteht, wenn das Eletron von der Schale n = 5 auf die Schale n = 2 abstürzt.
- Die blaugrüne Linie (486 nm) sendet ein Eletron aus, das vom Orbital n = 4 auf das Orbital n = 2 herunterfällt.
- und die rote Linie (656,3 nm) sendet ein Elektron aus, das vom Orbital n = 3 zum Orbital n = 2 übergeht.
- Wenn Elektronen auf das niedrigste Energieniveau (n = 1) herabfallen, wird so viel Energie frei, dass ultraviolette Strahlung entsteht, die wir mit bloßem Auge nicht sehen können.
Die Universität Wuppertal bietet auf ihrer Seite eine detailliertere Erklärung an. [4]
Wellenfunktionen sind komplexe Funktionen, die Zustände in der Natur beschreiben, die niemand je zu sehen bekommt.
Setzt man aber die Funktionen ins Quadrat, was passiert dann mit dem komplexen Anteil?
Ganz einfach: Da nach Definition i mal i gleich -1 ist, verschwindet der komplexe Anteil, und man erhält eine relle Zahl, die man als Messergebnis interpretieren und mit den Ergebnissen aus den Experimenten (z.B. dem Spektrum der Wasserstoffentladungslampe) vergleichen kann.
Die Physiker sagen dann auch: Die Wellenfunktion bricht zusammen.
Man kann es sich auch so klarmachen: Die Multiplikation der Wellenfunktion mit sich selbst beschreibt die Zerstörung des Quantensystems und den Übergang in ein anderes, und nur aus den Spuren der Zerstörung kann Erkenntnis über die Natur des vorher bestehenden und nachher entstandenen Systems gewonnen werden.
Vergleiche noch mal mit der Situation der Riesen, die ihre Atome, unsere Autos, ja auch nur erkennen können, indem sie sie zerstören.
Quantenphysikalische Begriffe und fragwürdige Aussagen dazu
Im Umgang mit der Quantenphysik kann man drei Ebenen unterscheiden:
- Die erste Ebene brachte der Physiker David Mermin 1989 so auf den Punkt: Shut up and calculate! - Halt den Mund! Rechne! [5] In dieser Perspektive geht es darum, die Ergebnisse von Messungen durch Berechnung als Element der Theorie zu bestätigen, ohne sich über die Natur der Sache, die man da misst, in irgendeiner Weise Gedanken zu machen. Dazu zähle ich auch die Möglichkeiten, die Ergebnisse der Berechnungen und Messungen anschaulich zu präsentieren, wie es in den vorhergehenden Kapiteln versucht wurde.
- Die zweite Ebene ist der Versuch der Physiker, die Objekte der Quantenphysik, meistens ausgehend von den Selbstverständlichkeiten der klassischen Physik, in irgendeiner Form in Begriffe zu fassen. Wenn oben von Wellenfunktion, Aufenthaltswahrscheinlichkeit usw. gesprochen wurde, waren das schon Beispiele dieser Physik-internen Interpretation, die über das bloße Berechnen und Messen hinausgehen. Weitere Begriffe gliedern in diesem Kapitel die Auseinandersetzung mit den mehr oder weniger zwingenden Folgerungen, die aus der Quantenphysik gezogen worden sind.
- Die dritte Ebene der Interpretation möchte etwas darüber aussagen, was die Einführung der Quantenphysik für das Verhältnis des Menschen zur Natur, zur Welt, zu sich selbst, zur Wissenschaft und zur Religion bedeuten könnte. Es sind wissenschaftstheoretische, naturphilosophische und esotherische Perspektiven, ohne dass die Abgrenzung besonders scharf wäre. Wir ordnen die Auseinandersetzung mit solchen Aussagen unten denjenigen Begriffen zu, an denen sie sich am leichtesten aufhängen lassen.
Unschärfe
Eine Messung kann nicht bestimmter sein, als der Gegenstand, den sie bestimmt. Die Warnung erinnert an Studenten, die drei Messwerte auf zwei Stellen hinter dem Komma gemessen haben, dann multiplizieren und glauben, das Resultat wäre auf sechs Nachkommastellen genau.
Die Grenze der Bestimmbarkeit in der Natur ist das Plancksche Wirkungsquantum.
Dieses beträgt 6,626 * 10-34 Joule * Sekunde.
Das Wirkungsquantum, das von Max Planck![]() (1858-1947) am 14. Dezember 1900 eingeführt wurde,[6] weshalb dieser Tag als Geburtstag der Quantenphysik gilt, beschreibt zunächst den Zusammenhang zwischen Frequenz (ny) und Energie (E) eines Photon:
(1858-1947) am 14. Dezember 1900 eingeführt wurde,[6] weshalb dieser Tag als Geburtstag der Quantenphysik gilt, beschreibt zunächst den Zusammenhang zwischen Frequenz (ny) und Energie (E) eines Photon:
E = h * ny
Das seinerzeit Verstörende an dieser Formel ist die Aussage, dass das Licht die Energie in "Paketen" transportiert. Zehn Jahre später entdeckte Robert Millikan![]() (1868-1953) die Elementarladung.[7] Das war die zweite Entdeckung einer "gequantelten" Messgröße. Die Bedeutung des Wirkungsquantums als Naturkonstante, die in allen atomaren Vorgängen eine Rolle spielt, hat sich erst nach und nach herausgestellt.
(1868-1953) die Elementarladung.[7] Das war die zweite Entdeckung einer "gequantelten" Messgröße. Die Bedeutung des Wirkungsquantums als Naturkonstante, die in allen atomaren Vorgängen eine Rolle spielt, hat sich erst nach und nach herausgestellt.
Werner Heisenberg![]() hat die Unschärferelation
hat die Unschärferelation![]() formuliert, die zum Ausdruck bringt, dass Messgrößen, deren Produkt eine Wirkung ist, nicht genauer bestimmt werden können als es dem Wirkungsquantum entspricht. Zwei Größen, deren Produkt eine Wirkung ist, sind zum Beispiel "Energie und Zeit", "Impuls und Ort". Heisenberg sprach von "komplementären Messgrößen", und sein Prinzip sagt aus, dass es keine Messmethode geben kann, die beide komplementären Messgrößen unendlich exakt bestimmt. Da das Wirkungsquantum eine so winzig kleine Größe hat, spielt das Unschärfeprinzip bei alltäglichen Messungen keine Rolle; irritierend für diejenigen, die von der klassischen Physik her kommen, ist allerdings die Tatsache, dass es nicht nur eine praktische, sondern auch eine prinzipielle Grenze der Messgenauigkeit gibt.
formuliert, die zum Ausdruck bringt, dass Messgrößen, deren Produkt eine Wirkung ist, nicht genauer bestimmt werden können als es dem Wirkungsquantum entspricht. Zwei Größen, deren Produkt eine Wirkung ist, sind zum Beispiel "Energie und Zeit", "Impuls und Ort". Heisenberg sprach von "komplementären Messgrößen", und sein Prinzip sagt aus, dass es keine Messmethode geben kann, die beide komplementären Messgrößen unendlich exakt bestimmt. Da das Wirkungsquantum eine so winzig kleine Größe hat, spielt das Unschärfeprinzip bei alltäglichen Messungen keine Rolle; irritierend für diejenigen, die von der klassischen Physik her kommen, ist allerdings die Tatsache, dass es nicht nur eine praktische, sondern auch eine prinzipielle Grenze der Messgenauigkeit gibt.
Boff / Hathaway behaupten in ihrem preisgekrönten Werk Befreite Schöpfung: Ein .. Merkmal des Quantenmikrokosmos ist der Zufallscharakter oder die Unbestimmtheit. .. Die Welt des linearen Determinismus löst sich mit dieser neuen Wirklichkeit tatsächlich auf, jedenfalls auf subatomarer Ebene. [8]
Determinismus![]() bezeichnet die Vorstellung, dass jetzt schon fest steht, was in Zukunft geschieht. Bei Johannes Calvin
bezeichnet die Vorstellung, dass jetzt schon fest steht, was in Zukunft geschieht. Bei Johannes Calvin![]() (1509-1564) war es eine logische Folgerung aus der Allmacht und Allwissenheit Gottes, dass die Bestimmung des Menschen zu Heil oder Unheil schon immer in Gottes Ratschluss beschlossen sei und der Mensch selbst nur noch nach Anzeichen der Vorhersehung forschen konnte. Die Physik des 19. Jahrhunderts pflegte den Glauben, der auf Robert Boyle
(1509-1564) war es eine logische Folgerung aus der Allmacht und Allwissenheit Gottes, dass die Bestimmung des Menschen zu Heil oder Unheil schon immer in Gottes Ratschluss beschlossen sei und der Mensch selbst nur noch nach Anzeichen der Vorhersehung forschen konnte. Die Physik des 19. Jahrhunderts pflegte den Glauben, der auf Robert Boyle![]() (1627-1692) zurückgeht, dass man nur einen Zustand der Welt exakt erfassen müsse, um alle Zustände zuvor und danach nach mathematischen Gesetzmäßigkeiten daraus ableiten zu können wie bei einem perfekten Uhrwerk.
(1627-1692) zurückgeht, dass man nur einen Zustand der Welt exakt erfassen müsse, um alle Zustände zuvor und danach nach mathematischen Gesetzmäßigkeiten daraus ableiten zu können wie bei einem perfekten Uhrwerk.
Die praktische Durchführung dieser Zurück- und Vorausberechnung scheitert an einer Reihe prinzipieller Hürden: Wie will man neben jedes "Atom" ein Messgerät stellen, und aus was sollen die Messgeräte denn bestehen? Wie kann man relle Zahlen, die dadurch definiert sind, dass sie unendlich viele unregelmäßig auftretende Stellen hinter dem Komma haben, je exakt bestimmen?
Und es ist ja nicht so, dass die Quantenphysik mit geringerer Messgenauigkeit arbeitet als die Physik des neunzehnten Jahrhunderts, im Gegenteil: Die genauesten Messungen, die Menschen heute durchführen, sind ohne die Nutzung von Quantenphänomenen nicht denkbar. Zum Beispiel setzt das Globale Positionierungssystem GPS![]() , mithilfe dessen jedes Smartphone "weiß", wo es sich gerade befindet, eine extrem genaue Messung der Zeit voraus, die nur mit Atomuhren realisiert werden kann.
, mithilfe dessen jedes Smartphone "weiß", wo es sich gerade befindet, eine extrem genaue Messung der Zeit voraus, die nur mit Atomuhren realisiert werden kann.
Es ist also nicht so, dass Vorhersagefähigkeiten, die die Menschen einmal besessen hätten, jetzt verschwunden wären. Richtig ist, dass eine Physik, die auf "Atome" und das Universum insgesamt anzuwenden zu Widersprüchen führt, durch Theorien ersetzt worden ist, die bislang widerspruchsfrei alle Experimente mit den kleinsten Bestandteilen der Materie erklären können, dafür aber den Nachteil der Unanschaulichkeit in Kauf nehmen. Das heißt: Es werden mathematisch Objekte definiert, die prinzipiell nicht in unserer Wahrnehmungswelt vorkommen können und sich nur durch Spuren in der Wahrnehmung verraten.
Verschränkung
Ein Vorurteil sagt, dass Quantenphysik vor allem mit dem ganz Kleinen zu tun hat. "Klein" ist aber vor allem das Plancksche Wirkungsquantum. Um von einem Quantensystem sprechen zu können, muss man die Bestandteile davor schützen, durch Einwirkungen größer oder gleich dem Wirkungsquantum gestört zu werden. Unter dieser Voraussetzung können ungestörte Quantensysteme sehr groß werden, wie Anton Zeilinger durch seine Experimente mit polarisiertem Licht gezeigt hat.[9]
Supraleitung![]() bedeutet, dass Strom ohne Widerstand fließt, weil die Ladungsträger durch extreme Kühlung in einem kohärenten Quantenzustand sind. Schaut man sich die supraleitenden Magnete am LHC in Genf an,[10] dann sieht man, dass kohärente Systeme sehr groß sein können.
bedeutet, dass Strom ohne Widerstand fließt, weil die Ladungsträger durch extreme Kühlung in einem kohärenten Quantenzustand sind. Schaut man sich die supraleitenden Magnete am LHC in Genf an,[10] dann sieht man, dass kohärente Systeme sehr groß sein können.
Es kommt also nicht auf die Größe in Zentimetern an, sondern auf die Kohärenz, die Ungestörtheit des Quantensystems.
Boff und Hathaway sagen: Das Phänomen, das man .. Quanten-Verschränkung nennt, tritt immer dann auf, wenn zwei Teilchen miteinander in Wechselwirkung treten. Von diesem Augenblick an bleiben sie für immer auf geheimnisvolle Weise miteinander verbunden. .. Das Phänomen der Verschränktheit verweist auf eine tiefe grundlegende Einheit, die den gesamten Kosmos auf Quantenebene verbindet.[11]
"Auf geheimnisvolle Weise miteinander verbunden" bleiben verschränkte Teilchen natürlich nur so lange, wie sie nicht gestört werden. Jede Art von Wechselwirkung zerstört die Verschränkung. Das bedeutet auch, dass man die Verschränkung nicht zur Informationsübertragung nutzen kann. Die "grundlegende Einheit des gesamten Kosmos auf Quantenebene" mag eine inspirierende Vorstellung sein, Ergebnis eines denkbaren Experimentes ist sie nicht. Die Quantenphysik ist keine spirituelle Unternehmung.
Das hindert die Physiker nicht daran, mit der Verschränkung zu experimentieren. Vielleicht werden diese Experimente einmal technische Anwendungen in der Quantenkryptografie, die eine absolut sichere Verschlüsselung von Daten verspricht, oder dem Quantencomputer finden. Anton Zeilinger![]() (*1945) hat eine Vorlesung über seine bahnbrechenden Experimente und ihre möglichen technischen Anwendungen gehalten.[12]
(*1945) hat eine Vorlesung über seine bahnbrechenden Experimente und ihre möglichen technischen Anwendungen gehalten.[12]
Tunneln
Superposition
- ↑ Albert Einstein schrieb 1926 in einem Brief an Max Born: Die Quantenmechanik ist sehr achtunggebietend. Aber eine innere Stimme sagt mir, daß das noch nicht der wahre Jakob ist. Die Theorie liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher. Jedenfalls bin ich überzeugt, daß der nicht würfelt. Näheres siehe: https://de.wikipedia.org/wiki/Gott_w%C3%BCrfelt_nicht
- ↑ Siehe dazu Ilya Prigogine, Isabelle Stengers: Dialog mit der Natur München (Piper) deutsch 6. Aufl. 1990; sieselben: Das Paradox der Zeit deutsch München (Piper) 1993.
- ↑ Meine Lehrbücher waren: Gerhard Gerlich: Eine neue Einführung in die statistischen und mathematischen Methoden des Quantentheorie, Braunschweig (vieweg) 1977 Das Vorlesungsskript von Heinrich Mitter Quantentheorie Mannheim (BI Hochschultaschenbücher) 1969, das heute Online zur Verfügung steht. Die legendären Vorlesungen von Richard Feynman (1918-1988) stehen heute ebenfalls in der Bearbeitung seiner Schüler online zur Verfügung: https://www.feynmanlectures.caltech.edu/
- ↑ http://www.hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/hyde.html#c4
- ↑ https://www.spektrum.de/kolumne/quantenphysik-ist-metaphysik-mit-physikalischen-mitteln/1703806
- ↑ Wer Max Planck etwas näher kennen lernen will, dem sein das folgende Video (44 MIN) empfohlen: https://www.youtube.com/watch?v=H0oKzF7bh3I
- ↑ Erklärung seines Öltröpfchenexperimentes: https://www.youtube.com/watch?v=P1jMNiiOUW8 (Video 5 MIN)
- ↑ Leonardo Boff/Mark Hathaway: Befreite Schöpfung aus dem Englischen von Bruno Kern, Kaevelaer 2016, 113 Gerhard Kruip weist in seiner Laudatio an Leonardo Boff zur Verleihung der Carl-Friedrich-von-Weizäcker Medaille 2016 ausdrücklich auf das Buch hin: https://www.cfvw.org/files/cfvw/pdf/laudatio_boff-gs.pdf
- ↑ Eine Video zeigt die Experimente zur Quantenteleportation, die Anton Zeilinger mit seinen Studenten in Wien durchgeführt hat: https://www.youtube.com/watch?v=MgM4-4_Dr1w
- ↑ in diesem Spektrum-Artikel ist ein Foto enthalten: https://www.spektrum.de/news/was-kommt-nach-dem-lhc/1733950
- ↑ Boff/Hathaway Befreite Schöpfung, 126
- ↑ Anton Zeilinger: Die zweite Quantenrevolution (Audiodatei mit Standbild 30 MIN): https://www.youtube.com/watch?v=RwOZGTFkDtY