Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Benutzer:HWollny/Quadratische Funktionen und ihre Graphen/Parameter e: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (72 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
= | =Stammgruppe 1, 2 und 3= | ||
{{Box|Info|Die Funktionen <math> | |||
}} | <gallery widths="200" heights="200" style="text-align:center"> | ||
Datei:En-11.png | |||
Datei:En-2.png | |||
Datei:En2.png | |||
Datei:En1.png | |||
</gallery> | |||
{{Box-spezial | |||
|Titel= Info | |||
|Inhalt= Die Funktionen, für die ihr Expertinnen und Experten seid, sind alles quadratische Funktionen der Form '''''<math>f(x)=x^2+e</math>'''''. | |||
Der Buchstabe '''e''' in der Funktionsgleichung wird '''Parameter''' genannt, d.h. wir können für e verschiedene Werte einsetzen und erhalten immer andere Funktionen. | |||
|Farbe= Üben | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #52A1AD | |||
|Hintergrund= #c4e3e8 | |||
}} | |||
<span class="brainy hdg-spech-bubbles fa-5x"></span> <u>Was passiert mit dem Graphen, wenn '''e''' sich verändert? </u> | |||
#Verändert in der GeoGebra-Datei mit Hilfe des Schiebereglers oder des Eingabefeldes die Größe des Parameters '''e''' und beobachtet, wie sich '''der Graph''' und die '''Funktionsgleichung''' verändern. | |||
#Diskutiert anschließend die Bedeutung des Parameters '''e''' in der Funktionsgleichung. | |||
<ggb_applet id="kkyrstwv" width="700" height="550" /> | |||
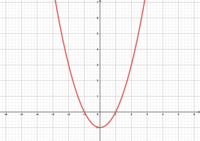
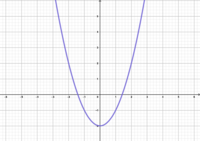
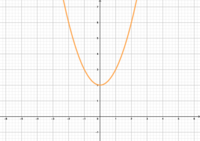
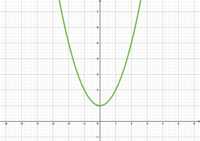
<span class="brainy hdg-spech-bubbles fa-5x"></span> '''<u>Welche Funktionsgleichung gehört zu welchem Graphen? </u>''' | |||
<gallery widths="200" heights="200" style="text-align:center"> | |||
Datei:En-11.png|mini|<small>Funktionsgleichung ?</small> | |||
Datei:En-2.png|mini|<small>Funktionsgleichung ?</small> | |||
Datei:En2.png|mini|<small>Funktionsgleichung ?</small> | |||
Datei:En1.png|mini|<small>Funktionsgleichung ?</small> | |||
</gallery> | |||
{{Box-spezial | |||
|Titel= <div align="center"> '''<math>f(x)=x^2-2</math>''' <span style="color:#C8C8C8"> hallo </span> <math>g(x)=x^2+1</math> <span style="color:#C8C8C8"> hallo </span> <math>h(x)=x^2+2</math> <span style="color:#C8C8C8"> hallo </span><math>k(x)=x^2-1</math> </div> | |||
|Inhalt= | |||
|Farbe= Üben | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #a0a0a0 | |||
|Hintergrund= #C8C8C8 | |||
}} | |||
#Ordnet gemeinsam euren Funktionsgraphen die passende Funktionsgleichung zu. Begründet kurz eure Entscheidungen. | |||
#Überprüft eure Zuordnung anschließend mithilfe von Geogebra. | |||
#Diskutiert die Lage der Graphen der Funktionen <math>f(x)=x^2+3</math> und <math>g(x)=x^2-4</math>, <span class="zum-farbe-Lernpfad">ohne</span> euch die Graphen anzuschauen. | |||
#Überprüft auch hier eure Vermutungen mithilfe von Geogebra. | |||
<ggb_applet id="kkyrstwv" width="700" height="550" /> | |||
<span class="brainy hdg-file02 fa-5x"></span> '''<u>Zusammenfassen der Erkenntnisse</u>''' | |||
Haltet eure Erkenntnisse über den Einfluss des Parameters '''e''' auf dem auf dem Arbeitsblatt zur Vorbereitung für die Expertenrunde fest. | |||
Nutzt als Beispiel die Funktion, für die ihr Expertin/Experte seid. | |||
<span class="brainy hdg-exclamation fa-2x"></span> | |||
*WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können. | |||
*Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus. | |||
<gallery widths="200" heights="200" style="text-align:center"> | |||
Datei:Vorbereitungsblatt.png | |||
</gallery> | |||
<span class="brainy hdg-space-shuttle fa-5x"></span> '''<u>Schon fertig?!</u>''' | |||
Ordnet zu, ob es sich bei der Funktion um eine nach oben oder nach unten verschobene Normalparabel handelt. | |||
Achtung: Manche Funktionen passen nicht dazu. | |||
{{LearningApp | |||
| app = pmpcrkoo522 | |||
| width = 100% | |||
| height = 400px | |||
}} | |||
Gebt den passenden Wert von '''e''' in den Funktionen an. | |||
{{LearningApp | |||
| app = p93zxk45n22 | |||
| width = 100% | |||
| height = 400px | |||
}} | |||
{{Fortsetzung | |||
|weiter=Parameter d | |||
|weiterlink=Benutzer:HWollny/Quadratische_Funktionen_und_ihre_Graphen/Parameter d | |||
|titel='''Lernpfad: Quadratische Funktionen und Ihre Gleichungen'''}} | |||
Aktuelle Version vom 18. August 2022, 18:47 Uhr
Stammgruppe 1, 2 und 3
Was passiert mit dem Graphen, wenn e sich verändert?
- Verändert in der GeoGebra-Datei mit Hilfe des Schiebereglers oder des Eingabefeldes die Größe des Parameters e und beobachtet, wie sich der Graph und die Funktionsgleichung verändern.
- Diskutiert anschließend die Bedeutung des Parameters e in der Funktionsgleichung.

Welche Funktionsgleichung gehört zu welchem Graphen?
- Ordnet gemeinsam euren Funktionsgraphen die passende Funktionsgleichung zu. Begründet kurz eure Entscheidungen.
- Überprüft eure Zuordnung anschließend mithilfe von Geogebra.
- Diskutiert die Lage der Graphen der Funktionen und , ohne euch die Graphen anzuschauen.
- Überprüft auch hier eure Vermutungen mithilfe von Geogebra.

Zusammenfassen der Erkenntnisse
Haltet eure Erkenntnisse über den Einfluss des Parameters e auf dem auf dem Arbeitsblatt zur Vorbereitung für die Expertenrunde fest. Nutzt als Beispiel die Funktion, für die ihr Expertin/Experte seid.
- WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können.
- Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus.
Schon fertig?!
Ordnet zu, ob es sich bei der Funktion um eine nach oben oder nach unten verschobene Normalparabel handelt. Achtung: Manche Funktionen passen nicht dazu.
Gebt den passenden Wert von e in den Funktionen an.
Lernpfad: Quadratische Funktionen und Ihre Gleichungen