Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Die Mittelsenkrechte: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Winkelhalbierende}}|Lernschritte einblenden|Lernschritte ausblenden}} | |||
__NOTOC__ | __NOTOC__ | ||
{{Box|1=Lernpfad|2=<h4>2. Streich: [[Mathematik-digital/Die Mittelsenkrechte|Die Mittelsenkrechte]]</h4> | {{Box|1=Lernpfad|2=<h4>2. Streich: [[Mathematik-digital/Die Mittelsenkrechte|Die Mittelsenkrechte]]</h4> | ||
===<u>Material:</u>=== | |||
*{{pdf|AB2_Mittelsenkrechte.pdf|Arbeitsblatt zur Mittelsenkrechten}} | *{{pdf|AB2_Mittelsenkrechte.pdf|Arbeitsblatt zur Mittelsenkrechten}}|3=Lernpfad}} | ||
{| | {| | ||
|[[bild:sägen.jpg|170px]] | |[[bild:sägen.jpg|170px]] | ||
| width="30px" | <br> | | width="30px" |<br> | ||
|''In der schönen Maienzeit,''<br> | |''In der schönen Maienzeit,''<br> | ||
''wenn die bayerischen Dorfesleut''<br> | ''wenn die bayerischen Dorfesleut''<br> | ||
| Zeile 24: | Zeile 24: | ||
''wo die Katzen oft 'rumschleichen''<br> | ''wo die Katzen oft 'rumschleichen''<br> | ||
''mittig zwischen den zwei Eichen'' | ''mittig zwischen den zwei Eichen'' | ||
| width = "30px" |<br> | | width="30px" |<br> | ||
| [[Bild:eichen.jpg|310px]] | |[[Bild:eichen.jpg|310px]] | ||
|} | |} | ||
| Zeile 41: | Zeile 41: | ||
==Was ist eine Mittelsenkrechte?== | ==Was ist eine Mittelsenkrechte?== | ||
{ | {{Box|1=Definition der Mittelsenkrechten|2= | ||
Eine Gerade heißt '''Mittelsenkrechte''' '''auf eine Strecke [AB]''', wenn sie durch den '''Mittelpunkt''' | Eine Gerade heißt '''Mittelsenkrechte''' '''auf eine Strecke [AB]''', wenn sie durch den '''Mittelpunkt''' | ||
der Strecke verläuft (die Strecke halbiert) und '''auf ihr senkrecht''' steht. | der Strecke verläuft (die Strecke halbiert) und '''auf ihr senkrecht''' steht. | ||
Sie wird mit '''m[AB]''' oder '''m<sub>AB</sub>''' bezeichnet. | Sie wird mit '''m[AB]''' oder '''m<sub>AB</sub>''' bezeichnet. | ||
Die Mittelsenkrechte auf eine Strecke ist eine '''Symmetrieachse''' dieser Strecke. | Die Mittelsenkrechte auf eine Strecke ist eine '''Symmetrieachse''' dieser Strecke. | ||
| | |3=Merksatz}} | ||
<ggb_applet width="350" height="250" id="g4rq8eww" showreseticon="true" /> | |||
{{Box|1=Notiere auf Deinem Arbeitsblatt|2= | {{Box|1=Notiere auf Deinem Arbeitsblatt|2= | ||
| Zeile 58: | Zeile 56: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
== Konstruktion der Mittelsenkrechten == | ==Konstruktion der Mittelsenkrechten== | ||
{{Box|1= | {{Box|1=|2= | ||
# Konstruieren mit Zirkel und Lineal die Mittelsenkrechte auf Deinem Arbeitsblatt! | # Konstruieren mit Zirkel und Lineal die Mittelsenkrechte auf Deinem Arbeitsblatt! | ||
# Notiere die besprochenen '''{{pdf|Konstruktion_Mittelsenkrecht.pdf|Konstruktionsschritte}}''' auf Dein Arbeitsblatt! | # Notiere die besprochenen '''{{pdf|Konstruktion_Mittelsenkrecht.pdf|Konstruktionsschritte}}''' auf Dein Arbeitsblatt! | ||
| Zeile 74: | Zeile 72: | ||
== Puzzle zur Mittelsenkrechten == | ==Puzzle zur Mittelsenkrechten== | ||
'''[http://inmare.cspsx.de/Mittelsenkrechte.htm Zuordungspuzzle]''': '''Ordne die jeweiligen "Schatzkarten" den Beschreibungen zu!'''<br><br> | '''[http://inmare.cspsx.de/Mittelsenkrechte.htm Zuordungspuzzle]''': '''Ordne die jeweiligen "Schatzkarten" den Beschreibungen zu!'''<br><br> | ||
== Wiederholung == | ==Wiederholung== | ||
''Für kühles Eis in der Sommerzeit,''<br> | ''Für kühles Eis in der Sommerzeit,''<br> | ||
| Zeile 84: | Zeile 82: | ||
''wo sie wohl eine Eisdiele hat?''<br> | ''wo sie wohl eine Eisdiele hat?''<br> | ||
<ggb_applet width="540" height="530" | <ggb_applet width="540" height="530" id="qn7qwndh" showtoolbar="true" showreseticon="true" /> | ||
{{Box|1=Aufgabe|2= | {{Box|1=Aufgabe|2= | ||
| Zeile 97: | Zeile 94: | ||
==Weitere Aufgaben und Hausaufgabe== | |||
== Weitere Aufgaben und Hausaufgabe == | |||
Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:<br> | Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:<br> | ||
'''S. 20 / Nr. 22, 23 und 25a)''' | '''S. 20 / Nr. 22, 23 und 25a)''' | ||
| Zeile 105: | Zeile 101: | ||
<div align="center"><font><b>''Dies nun war der zweite Streich und der dritte folgt zugleich!''</b></font></div> | <div align="center"><font><b>''Dies nun war der zweite Streich und der dritte folgt zugleich!''</b></font></div> | ||
{{Fortsetzung|weiter=Das Lot|weiterlink=Das_Lot}} | |||
{{ | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
[[Kategorie: | [[Kategorie:Lernpfad]] | ||
[[Kategorie: | [[Kategorie:Mathematik-digital]] | ||
[[Kategorie:Interaktive Übung]] | |||
Aktuelle Version vom 24. April 2022, 10:06 Uhr
Lernpfad
Aufgabe
Betrachte die obige Skizze der beiden Eichen.
- Überlege zunächst, welche besonderen Eigenschaften der Maibaum von Max und Moritz besitzen muss.
- Welche besonderen Eigenschaften besitzt die rote Gerade? Überlege wie man aufgrund ihrer geometrischen Eigenschaft diese konstruieren kann!
- Konstruiere (auf einem Notizblatt) zwischen zwei beliebigen Punkten eine Mittelsenkrechte!
- Überprüfe Deine Konstruktionsschritte anhand folgender animierten Konstruktion!
- Formuliere die einzelnen Konstruktionsschritte schriftlich auf einem Übungszettel! Überprüfe die Konstruktionsschritte mit Deinem Nachbarn!
Was ist eine Mittelsenkrechte?
Definition der Mittelsenkrechten
Eine Gerade heißt Mittelsenkrechte auf eine Strecke [AB], wenn sie durch den Mittelpunkt der Strecke verläuft (die Strecke halbiert) und auf ihr senkrecht steht. Sie wird mit m[AB] oder mAB bezeichnet.
Die Mittelsenkrechte auf eine Strecke ist eine Symmetrieachse dieser Strecke.
Notiere auf Deinem Arbeitsblatt
- Übertrage die Definition der Mittelsenkrechten auf Dein Arbeitsblatt!
- Wann kommt in der Natur oder im Alltag eine Mittelsenkrechte vor? Überlege Dir mindestens drei weitere Beispiele!
Konstruktion der Mittelsenkrechten
- Konstruieren mit Zirkel und Lineal die Mittelsenkrechte auf Deinem Arbeitsblatt!
- Notiere die besprochenen
 Konstruktionsschritte auf Dein Arbeitsblatt!
Konstruktionsschritte auf Dein Arbeitsblatt!
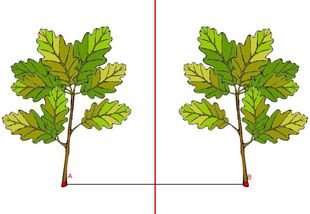
Aufgabe - Konstruktion mit Geogebra
- Öffne die
 GeoGebra-Datei mit zwei Eichen, am Punkt A und am Punkt B.
GeoGebra-Datei mit zwei Eichen, am Punkt A und am Punkt B. - Konstruiere die Mittelsenkrechte auf die Strecke [AB], die beide Eichen miteinander verbindet!
- Speichere die Datei unter dem Namen "Mittelsenkrechte_<<DeinName>>" im Klassenverzeichnis auf der Festplatte ab!

Puzzle zur Mittelsenkrechten
Zuordungspuzzle: Ordne die jeweiligen "Schatzkarten" den Beschreibungen zu!
Wiederholung
Für kühles Eis in der Sommerzeit,
sind Max und Moritz zu allem bereit.
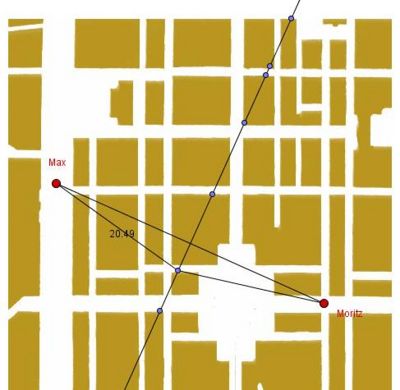
Rechts der Stadtplan ihrer Stadt,
wo sie wohl eine Eisdiele hat?

Aufgabe
Zeichne alle möglichen Eisdielen in den Stadtplan ein, die von Max und Moritz (Luftlinie!) gleich weit entfernt sind!
- Konstruiere die Menge aller Punkte, die von Max und Moritz (Luftlinie!) gleich weit entfernt sind!
- Weiß eingezeichnet sind die Straßen, braun mögliche Gebäudekomplexe. Trage in GeoGebra diejenigen Punkte ein, die (Luftlinie!) von Max und Moritz gleich weit entfernt sind und an denen sich eine Eisdiele befinden könnte!
- Wie weit ist die nächste Eisdiele (Luftlinie!) von beiden entfernt?
- Wer von beiden hat den weiteren Weg zur Eisdiele?
Weitere Aufgaben und Hausaufgabe
Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:
S. 20 / Nr. 22, 23 und 25a)
Dies nun war der zweite Streich und der dritte folgt zugleich!