Vera 8 interaktiv/Mathematik/Test A: Unterschied zwischen den Versionen
(angelegt) |
Keine Bearbeitungszusammenfassung |
||
| (127 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[http://www.iqb.hu-berlin.de/bista/aufbsp/vera8_2009/Mathematik_Testheft_A.pdf '''Testheft A zum Download'''] | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 1: Umkehraufgabe'''</big> | <big>'''Aufgabe 1: Umkehraufgabe'''</big> | ||
| Zeile 27: | Zeile 7: | ||
</div> | </div> | ||
<div class="rahmen"> | |||
<big>''' Aufgabe 2: Stadion'''</big> | |||
Ein Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze <br />und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €. | |||
Ein Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €. | |||
Wie viel Geld nimmt der Verein bei einem vollen Stadion ein? | Wie viel Geld nimmt der Verein bei einem vollen Stadion ein? | ||
{{Lösung versteckt | |||
'''120 700 Euro''' | |1='''120 700 Euro''' | ||
*5300 Sitzplätze · 14 Euro/Sitzplatz = 74200 Euro | |||
*9300 Stehplätze · 5 Euro/Stehplatz = 46500 Euro | |||
*74200 Euro + 46500 Euro = 120700 Euro | |||
}} | }} | ||
</div> | </div> | ||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 3: Basketball'''</big> | <big>'''Aufgabe 3: Basketball'''</big> | ||
| Zeile 56: | Zeile 32: | ||
</div> | </div> | ||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 4: Zapfsäule 1'''</big> | <big>'''Aufgabe 4: Zapfsäule 1'''</big> | ||
[[Bild:AufgabeA4_Zapfsäule.jpg|400px|center]] | [[Bild:AufgabeA4_Zapfsäule.jpg|400px|center]] | ||
Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. | Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. | ||
| Zeile 64: | Zeile 40: | ||
Kreuze die richtige Antwort an. | Kreuze die richtige Antwort an. | ||
(!15,80€) (!34,47€) (42,71€) (!73,-€) (!90,45€) | |||
</div> | |||
<div class="rahmen"> | |||
< | |||
<big>'''Aufgabe 4: Zapfsäule 2 '''</big> | <big>'''Aufgabe 4: Zapfsäule 2 '''</big> | ||
| Zeile 75: | Zeile 50: | ||
Erkläre, wie Petra zu dieser Aussage kommt. | Erkläre, wie Petra zu dieser Aussage kommt. | ||
{{Lösung versteckt | |||
|1=*1 Euro - 73 Cent = 27 Cent, das entspricht ca. 25% bzw. 1/4. | |||
*73 Cent pro Euro bedeutet 73% Steuern, also etwa 3/4. Also etwas 1/4 ohne Steuern. | |||
}} | }} | ||
</div> | </div> | ||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 5: Kreis'''</big> | <big>'''Aufgabe 5: Kreis'''</big> | ||
[[Bild:AufgabeA5_Kreis.jpg|200px|center]] | [[Bild:AufgabeA5_Kreis.jpg|200px|center]] | ||
| Zeile 89: | Zeile 63: | ||
Kreuze die richtige Lösung an. | Kreuze die richtige Lösung an. | ||
(!30%) (!45 | (!30%) (!45%) (!60%) (!70%) (75%) (!95%) | ||
</div> | </div> | ||
<div class="rahmen"> | |||
<big>'''Aufgabe 6: Gleichung '''</big> | |||
<big>'''Aufgabe 6 | |||
Du siehst hier folgende Aufgabe: 248 + 146 + 320 = | Du siehst hier folgende Aufgabe: 248 + 146 + 320 = | ||
| Zeile 101: | Zeile 74: | ||
Erkläre, warum das so ist, ohne das Ergebnis auszurechnen. | Erkläre, warum das so ist, ohne das Ergebnis auszurechnen. | ||
{{Lösung versteckt|1=zum Beispiel: | |||
* 248, 146, 320 sind gerade Zahlen. werden diese Zahlen addiert, dann ist auch das Ergebnis eine gerade Zahl'' | |||
* In den Zahlen sind nur gerade Zahlen.'' | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 7: Welche Zahl fehlt?'''</big> | |||
Trage die fehlende Zahl ein! | |||
'''1.''' [[Bild:AufgabeA7_Zahl1.jpg|300px]] | |||
'''2.''' [[Bild:AufgabeA7_Zahl2.jpg|300px]] | |||
{{Lösung versteckt | |||
| | |||
#49 | |||
#275 | |||
}} | |||
'''3.''' Timo schreibt die Zahl 64 zur 31. Das ist die richtige Lösung! Schreibe auf, wie Timo die Zahl 64 gefunden hat. | |||
[[Bild:AufgabeA7_Zahl3.jpg|300px]] | |||
{{Lösung versteckt| | |||
''"Obere Zahl mal 2 und dann plus 2"'' oder ''"Obere Zahl plus 1 und dann mal 2"'' | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 8: Ziffer 5'''</big> | |||
Peter hat nacheinander alle Zahlen von 1 bis 99 notiert. | |||
Wie oft hat er dabei die Ziffer 5 geschrieben? | |||
{{Lösung versteckt| | |||
20 mal | |||
}} | |||
Wie viele Ziffern hat Peter insgesamt geschrieben? | |||
{{Lösung versteckt| | |||
189 Ziffern | |||
}} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 9: Rechteck'''</big> | |||
Ein Rechteck ist 4 cm lang und 3 cm breit. | |||
[[Bild:AufgabeA9_Rechteck.jpg|300px|center]] | |||
Wie groß ist sein Flächeninhalt? | |||
Kreuze an. | |||
(12cm<sup>2</sup>) (!7 cm) (!7 cm<sup>2</sup>) (!12 cm) (!14 cm) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 10: Puzzleteile'''</big> | |||
Welches dieser Puzzleteile hat den größten Flächeninhalt? Kreuze an. | |||
(![[Bild:AufgabeA10_Puzzle1.jpg|100px]]) (![[Bild:AufgabeA10_Puzzle2.jpg|100px]]) (![[Bild:AufgabeA10_Puzzle3.jpg|100px]]) (![[Bild:AufgabeA10_Puzzle4.jpg|100px]]) ([[Bild:AufgabeA10_Puzzle5.jpg|100px]]) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 11: Saft'''</big> | |||
Für wie viele Gläser reicht die Flasche? | |||
[[Bild:AufgabeA11_Saft.jpg|300px]] | |||
{{Lösung versteckt| | |||
Die Flasche reicht für '''10''' Gläser Saft. | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 12: Das unmögliche Dreieck'''</big> | |||
Begründe, warum es kein Dreieck mit diesen Maßen geben kann. | |||
[[Bild:AufgabeA12_Dreieck.jpg|300px|center]] | |||
{{Lösung versteckt| | |||
z.B.: ''Das Dreieck ABC ist gleichschenklig und hat einen Innenwinkel von 60<sup>0</sup>. Folglich müsste dieses Dreieck gleichseitig sein. Daher müssten alle Seiten entweder 39,5 cm oder 45 cm lang sein.'' | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 13: Geld umrechnen'''</big> | |||
Rechne um: | |||
27 € 50 Cent = ..... '''Euro''' | |||
{{Lösung versteckt|1= | |||
27 € 50 Cent =''' 27,50 Euro''' | |||
}} | |||
1 € 1 Cent = ..... '''Cent''' | |||
{{Lösung versteckt|1= | |||
1 € 1 Cent = '''101 Cent''' | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 14: Minuten und Sekunden'''</big> | |||
Rechne die Zeitangaben um und fülle die Lücken aus. ''Beispiel: 95 s = '''1''' min '''35'''s'' | |||
..... s = 3 min 28 s | |||
{{Lösung versteckt | |||
|1='''208 s''' = 3 min 28 s | |||
}} | |||
136 s = ..... min ..... s | |||
{{Lösung versteckt | |||
|1=136 s = '''2''' min '''16''' s | |||
}} | |||
..... s = 8 min 20 s | |||
{{Lösung versteckt|1= | |||
'''500''' s = 8 min 20 s | |||
}} | |||
</div> | |||
<div class="zuordnungs-quiz"> | |||
<big>'''Aufgabe 15: Fehlendes Zeichen'''</big> | |||
Ordne zu: | |||
{| | |||
|<||5m ... 5,50 m||0, 8 cm ... 100 mm | |||
|- | |||
|>||20 cm ... 20 mm||700 cm ... 17 cm | |||
|- | |||
|=||180 cm ... 1,80 m||4 cm ... 40 mm | |||
|} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 16: Winkel im Dreieck'''</big> | |||
In einem gleichschenkligen Dreieck ist der Winkel <math>\gamma</math> an der Spitze dreimal so groß wie ein Basiswinkel <math>\alpha</math>. | |||
Wie groß sind die Winkel dieses Dreiecks? Kreuze die richtige Antwort an. | |||
(!<math>\alpha=30^\circ; \gamma = 90^\circ</math>) (!<math>\alpha=30^\circ; \gamma = 90^\circ</math>) (<math>\alpha=36^\circ; \gamma = 108^\circ</math>) (!<math>\alpha=22,5^\circ; \gamma = 135^\circ</math>) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 17: Nachbarseiten im Parallelogramm'''</big> | |||
Bei einem Parallelogramm ist eine Seite 40 cm lang und eine banachbarte Seite 90 cm. Wie groß ist der Umfang des Parallelogramms? | |||
Kreuze an. | |||
(!130 cm) (!170 cm) (260 cm) (!340 cm) (!360 cm) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 18: Fahrplan'''</big> | |||
Hier siehst du den Fahrplan von Köln mit dem Intervity IC 800 nach Hamburg. | |||
<div align="center"> | |||
{| class="wikitable" | |||
!Bahnhof | |||
!an | |||
!ab | |||
|- | |||
|Köln Hbf | |||
| | |||
|10:09 | |||
|- | |||
|Düsseldorf Hbf | |||
|10:30 | |||
|10:32 | |||
|- | |||
|Duisburg Hbf | |||
|10:44 | |||
|10:46 | |||
|- | |||
|Essen Hbf | |||
|10:57 | |||
|10:59 | |||
|- | |||
|Bochum Hbf | |||
|11:07 | |||
|11:09 | |||
|- | |||
|Dortmund Hbf | |||
|11:20 | |||
|11:24 | |||
|- | |||
|Münster (Westf) Hbf | |||
|11:53 | |||
|11:55 | |||
|- | |||
|Osnabrück Hbf | |||
|12:18 | |||
|12:20 | |||
|- | |||
|Bremen Hbf | |||
|13:13 | |||
|13:15 | |||
|- | |||
|Hamburg - Harburg | |||
|13:59 | |||
|14:01 | |||
|- | |||
|Hamburg Hbf | |||
|14:09 | |||
| | |||
|} | |||
</div> | |||
<br> | |||
#Wie lange braucht der Zug von Köln bis Hamburg Hbf? | |||
#Her Schmitz fährt von Essen nach Bremen. Wie lange braucht der Zug für diese Strecke? | |||
#Frau Krüger fährt von Köln nach Münster. Wie lange braucht der Zug für diese Strecke? | |||
#An welchem Bahnhof hält der Zug am längsten? | |||
{{Lösung versteckt| | |||
:#4 Stunden ''oder'' 240 Minuten | |||
:#2 Stunden 14 Minuten ''oder'' 134 Minuten | |||
:#1 Stunde 44 Minuten ''oder'' 104 Minuten | |||
:#Dortmund | |||
|Lösung anzeigen|Lösung verbergen}} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 19: Fadenaufgabe'''</big> | |||
Ein 34 Zentimeter langer Faden wird zu einem Rechteck gelegt. Die Breite des Rechteckes beträgt 8 Zentimeter. Wie lang ist das Rechteck? | |||
(!8 Zentimeter) (9 Zentimeter) (!13 Zentimeter) (!18 Zentimeter) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 20.1: Museum'''</big> | |||
Eine neue Sonderausstellung ist eröffnet worden. Die Besucherzahlen der ersten Woche kannst du der Grafik entnehmen: | |||
[[Bild:AufgabeA20_Museum.jpg|500px|center]] | |||
An welchem Wochentag kamen die meisten Besucher? | |||
{{Lösung versteckt| | |||
Freitag | |||
}} | }} | ||
</div> | </div> | ||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 20.2: Museum'''</big> | |||
Bestimme mit der Grafik aus 20.1, wie viele Personen im Schnitt pro Besuchstag die Ausstellung gesehen haben. | |||
Kreuze an, welcher Wert deinem Ergebnis am nächsten liegt. | |||
(!289) (!328) (337) (!344) (!381) | |||
</div> | </div> | ||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 21: Körpertemperatur'''</big> | |||
Oliver liegt im Krankenhaus. Da er mit hohem Fieber eingeliefert wurde, wird mehrmals am Tag seine Körpertemperatur gemessen. | |||
{| class="wikitable" | |||
! | |||
!6 Uhr | |||
!9 Uhr | |||
!12 Uhr | |||
!15 Uhr | |||
!20 Uhr | |||
|- | |||
|'''Sonntag''' | |||
| - | |||
| - | |||
|39,8<sup>0</sup> | |||
|39,7<sup>0</sup> | |||
|39,9<sup>0</sup> | |||
|- | |||
|'''Montag''' | |||
|38,5<sup>0</sup> | |||
|38,1<sup>0</sup> | |||
|38,0<sup>0</sup> | |||
|38,2<sup>0</sup> | |||
|38,5<sup>0</sup> | |||
|- | |||
|'''Dienstag''' | |||
|37,9<sup>0</sup> | |||
|37,9<sup>0</sup> | |||
|38,1<sup>0</sup> | |||
|38,3<sup>0</sup> | |||
|38,3<sup>0</sup> | |||
|- | |||
|'''Mittwoch''' | |||
|37,3<sup>0</sup> | |||
|37,5<sup>0</sup> | |||
|37,7<sup>0</sup> | |||
|37,6<sup>0</sup> | |||
|37,4<sup>0</sup> | |||
|} | |} | ||
Wann wurde die '''höchste''' Temperatur gemessen? Kreuze an. | |||
(!Montag, 6 Uhr) (!Montag, 9 Uhr) (!Dienstag, 15 Uhr) (Sonntag, 20 Uhr) | |||
Wann wurde die '''niedrigste''' Temperatur gemessen? Kreuze an. | |||
(!Montag, 12 Uhr) (!Dienstag, 6 Uhr) (Mittwoch, 6 Uhr) (!Mittwoch, 20 Uhr) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 22: Münzwurf'''</big> | |||
Wenn eine Münze geworfen wird, beträgt die Wahrscheinlichkeit, dass die Zahl oben liegt, <math>\frac{1}{2}</math>. | |||
[[Bild:AufgabeA22_Münzwurf.jpg|400px|center]] | |||
In drei aufeinander folgenden Würfen landet die Münze jedes Mal so, dass die Zahl oben ist. Welche der vier Aussagen trifft für den vierten Wurf zu? | |||
Kreuze die richtige Aussage an. | |||
(!Es ist wahrscheinlicher, dass der Adler oben liegt.) (!Es ist wahrscheinlicher, dass die Zahl oben liegt.) (Es ist gleich wahrscheinlich, dass Zahl oder Adler oben liegt.) (!Um die Frage zu beantworten, braucht man noch mehr Informationenen.) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 23: Spielsteine'''</big> | |||
Eine Kiste enthält 45 farbige Spielsteine: blaue, grüne und gelbe. Wenn die Wahrscheinlichkeit, einen gelben zu ziehen, <math>\frac{2}{5}</math> beträgt, wie viele gelbe Spielsteine sind dann in der Kiste? Kreuze an. | |||
(!2) (!5) (! 9) (18) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 24: Rotblauer Würfel'''</big> | |||
Jede der sechs Flächen eines Würfels ist angemalt. Einige Flächen sind rot und einige Flächen sind blau. Beim Würfeln ist die Wahrscheinlichkeit, dass eine rote Fläche oben liegen bleibt, <math>\frac{2}{3}</math>. Wie viele Flächen des Würfels sind rot angemalt? Kreuze an. | |||
(!eine) (!zwei) (! drei) (vier) (! fünf) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 25.1: Wertetabelle'''</big> | |||
Kevin berechnet folgende Wertetabelle einer linearen Funktion. Der letzte y-Wert fehlt noch. | |||
{| cellspacing="0" cellpadding="15" border="1" | |||
|'''x'''||2||3||4||5||6 | |||
|- | |||
|'''y'''||7||10||13||16||... | |||
|} | |||
Ermittle den fehlenden y-Wert und trage ihn in die Tabelle ein. | |||
{{Lösung versteckt| | |||
19 | |||
}} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 25.2: Wertetabelle'''</big> | |||
Welche Gleichung gehört zu der Wertetabelle, die Kevin berechnet hat (''siehe Aufgabe 25.1'')? Kreuze an. | |||
(!y = x + 5) (!y = x - 5) (! y = 4x - 1) (y = 3x + 1) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 26: Gleichung'''</big> | |||
Gegeben ist die Gleichung 6x = 4,2. Bestimme x. | |||
{{Lösung versteckt|1= | |||
x = 0,7 | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 27: Postkarten'''</big> | |||
Martin und Uta kaufen Postkarten. Die Postkarten haben alle den gleichen Preis. Uta kauft neun Karten, Martin kauft sechs Karten. | |||
Die Postkarten kosten zusammen 9,00€. Wie viel bezahlt Uta? | |||
{{Lösung versteckt|1= | |||
Uta bezahlt 5,40 Euro. | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 28: Koordinatensystem'''</big> | |||
1. Zeichne den Punkt A (2|3) in das Koordinatensystem ein. | |||
[[Bild:AufgabeA28_Koordinatensystem1.jpg|200px|center]] | |||
{{Lösung versteckt | |||
|'''1.''' [[Bild:AufgabeA28_Koordinatensystem1_Lös.jpg|200px|center]] | |||
}} | |||
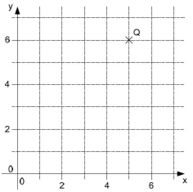
2. Trage die Koordinaten des Punktes Q ein. | |||
[[Bild:AufgabeA28_Koordinatensystem2.jpg|193px|center]] | |||
{{Lösung versteckt|1= | |||
'''2.''' Q(5/6) | |||
}} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 29: Spiegelung'''</big> | |||
[[Bild:AufgabeA29_Spiegelung.jpg|150px]] | |||
Das graue Dreieck wird an der Achse a gespiegelt. | |||
Welche der Figuren stellt das Ergebnis der Spiegelung dar? Kreuze an. | |||
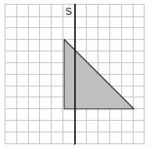
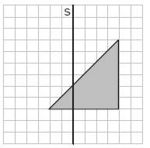
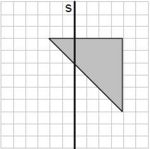
(![[Bild:AufgabeA29_Spiegelung1.jpg|150px]]) ([[Bild:AufgabeA29_Spiegelung2.jpg|150px]]) (![[Bild:AufgabeA29_Spiegelung3.jpg|150px]]) (![[Bild:AufgabeA29_Spiegelung4.jpg|150px]]) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
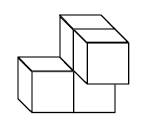
<big>'''Aufgabe 30: Würfelnetze'''</big> | |||
[[Bild:AufgabeA30_Würfelnetze.jpg|100px|left]] | |||
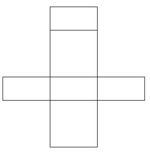
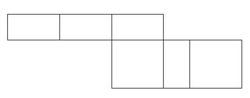
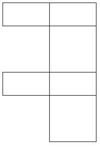
Welches der vier Netze ergibt beim Zusammenfalten den oben abgebildeten Würfel? Kreuze an. | |||
(![[Bild:AufgabeA30_Würfelnetze1.jpg|150px]]) (![[Bild:AufgabeA30_Würfelnetze2.jpg|150px]]) ([[Bild:AufgabeA30_Würfelnetze3.jpg|150px]]) (![[Bild:AufgabeA30_Würfelnetze4.jpg|150px]]) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 31: Symmetrieachsen im Trapez'''</big> | |||
Welche Zeichnung zeigt '''alle''' Symmetrieachsen eines gleichschenkligen (symmetrischen) Trapezes? Kreuze an. | |||
(![[Bild:AufgabeA31_Trapez1.jpg|150px]]) (![[Bild:AufgabeA31_Trapez2.jpg|150px]]) ([[Bild:AufgabeA31_Trapez3.jpg|150px]]) (![[Bild:AufgabeA31_Trapez4.jpg|150px]]) | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 32: Spiegelachse'''</big> | |||
Das Dreieck A'B'C' ist das Ergebnis einer Achsenspiegelung des Dreiecks ABC. | |||
Zeichne die Spiegelachse g ein. | |||
[[Bild:AufgabeA32_Spiegelachse.jpg|350px|center]] | |||
{{Lösung versteckt| | |||
[[Bild:AufgabeA32_Spiegelachse_Lös.jpg|350px|center]] | |||
}} | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 33: Parallelogramme'''</big> | |||
Welche dieser Aussagen, die für alle Parallelogramme gelten sollen, ist '''FALSCH'''? | |||
Kreuze an. | |||
(!Gegenüberliegende Seiten sind parallel.) | |||
(!Die Diagonalen halbieren sich gegenseitig.) | |||
(!Gegenüberliegende Winkel sind gleich groß.) | |||
(Es gibt genau eine Spiegelachse.) | |||
(!Gegenüberliegende Seiten sind gleich lang.) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 34: Kongruente Figuren'''</big> | |||
Gegeben ist eine Figur.[[Bild:AufgabeA34_Kongruenz.jpg|50px]] | |||
Welche der unten stehenden Figuren ist nicht kongruent (deckungsgleich) zu der oben gegebenen Figur? | |||
(![[Bild:AufgabeA34_Kongruenz1.jpg|90px]]) (![[Bild:AufgabeA34_Kongruenz2.jpg|90px]]) (![[Bild:AufgabeA34_Kongruenz3.jpg|80px]]) (![[Bild:AufgabeA34_Kongruenz4.jpg|90px]]) ([[Bild:AufgabeA34_Kongruenz5.jpg|80px]]) (![[Bild:AufgabeA34_Kongruenz46.jpg|80px]]) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 35: Würfel drehen'''</big> | |||
Dieser Körper wird in eine andere Lage gedreht: | |||
[[Bild:AufgabeA35_Würfel.jpg|150px]] | |||
Welches der folgenden Bilder zeigt den gedrehten Körper? Kreuze an. | |||
(![[Bild:AufgabeA35_Würfel1.jpg||150px]]) (![[Bild:AufgabeA35_Würfel2.jpg||150px]]) ([[Bild:AufgabeA35_Würfel3.jpg||150px]]) (![[Bild:AufgabeA35_Würfel4.jpg||150px]]) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 36: Spiegelschrift'''</big> | |||
[[Bild:AufgabeA36_Spiegelschrift.jpg|100px]] | |||
Du hältst dieses Schild so vor dich, dass jeder es lesen kann, und stehst vor einem Spiegel. Was siehst du? Kreuze an. | |||
(![[Bild:AufgabeA36_Spiegelschrift1.jpg|100px]]) (![[Bild:AufgabeA36_Spiegelschrift2.jpg|100px]]) (![[Bild:AufgabeA36_Spiegelschrift3.jpg|100px]]) (![[Bild:AufgabeA36_Spiegelschrift4.jpg|100px]]) | |||
([[Bild:AufgabeA36_Spiegelschrift5.jpg|100px]]) | |||
</div> | |||
<div class="multiplechoice-quiz"> | |||
<big>'''Aufgabe 37: Quadernetze'''</big> | |||
Welches der vier Netze ergibt beim Zusammenfalten '''keinen''' Quader? Kreuze an. | |||
(![[Bild:AufgabeA37_Quadernetz1.jpg|150px]]) (![[Bild:AufgabeA37_Quadernetz2.jpg|250px]]) ([[Bild:AufgabeA37_Quadernetz3.jpg|100px]]) (![[Bild:AufgabeA37_Quadernetz4.jpg|150px]]) | |||
</div> | |||
<div class="zuordnungs-quiz"> | |||
<big>'''Aufgabe 38: Gleichschenklige Dreiecke'''</big> | |||
Sind folgende Aussagen wahr oder falsch? | |||
<span style="background:yellow">Jedes gleichschenklige Dreieck ...</span> | |||
{| | |||
|wahr||... besitzt mindestens eine Symmetrieachse.||... hat mindestens zwei gleich große Winkel. | |||
|- | |||
|falsch||...besitzt drei gleich lange Seiten.||... hat immer einen rechten Winkel. | |||
|} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 39: Punkte und Abstände'''</big> | |||
Gegeben sind zwei Halbgeraden g und h und ein Punkt P. | |||
[[Bild:AufgabeA39_Abstand.jpg|300px|center]] | |||
Zeichne eine Senkrechte durch den Punkt P auf die Halbgerade g und eine Senkrechte durch den Punkt P auf die Halbgerade h. | |||
{{Lösung versteckt|1= | |||
[[Bild:AufgabeA39_Abstand_Lös.jpg|300px|center]] | |||
}} | |||
</div> | |||
<div class="rahmen"> | |||
<big>'''Aufgabe 40: Dreieck'''</big> | |||
In einem gleichschenkligen Dreieck ist die Basis doppelt so lang wie die Höhe. Wie groß sind die Winkel dieses Dreiecks? | |||
{{Lösung versteckt| | |||
45<sup>0</sup>, 45<sup>0</sup> und 90<sup>0</sup> | |||
}} | |||
</div> | |||
__NOEDITSECTION__ | |||
{{DEFAULTSORT:Mathematik/Test A}} | |||
[[Kategorie:Vera 8]] | |||
[[Kategorie:Vergleichsarbeiten]] | |||
[[Kategorie:Mathematik-digital]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 17:55 Uhr
Aufgabe 1: Umkehraufgabe
Zu welcher Zahl muss man 6345 addieren, um 8567 zu erhalten? (!2023) (2222) (!1987) (!14912)
Aufgabe 2: Stadion
Ein Fußballstadion hat 14600 Plätze, davon sind 5300 Sitzplätze
und 9300 Stehplätze. Ein Sitzplatz kostet 14,00 € und ein Stehplatz 5,00 €.
Wie viel Geld nimmt der Verein bei einem vollen Stadion ein?
120 700 Euro
- 5300 Sitzplätze · 14 Euro/Sitzplatz = 74200 Euro
- 9300 Stehplätze · 5 Euro/Stehplatz = 46500 Euro
- 74200 Euro + 46500 Euro = 120700 Euro
Aufgabe 3: Basketball
Bei einem Basketball-Turnier einer Hauptschule nehmen vier achte Klassen, fünf neunte Klassen und zwei zehnte Klassen teil.
Die Klassen werden in der Vorrunde in zwei Gruppen (Gruppe A und Gruppe B) aufgeteilt. Jede Klasse einer Gruppe spielt gegen jede andere Klasse dieser Gruppe. Fünf Klassen sind in der Gruppe A. Wie viele Spiele finden in der Vorrunde in Gruppe A statt? Kreuze an:
(!5 Spiele) (10 Spiele) (!15 Spiele) (!25 Spiele)
Aufgabe 4: Zapfsäule 1
Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. Wie viel erhält der Staat bei der dargestellten Tankfüllung an Steuern? Kreuze die richtige Antwort an.
(!15,80€) (!34,47€) (42,71€) (!73,-€) (!90,45€)
Aufgabe 4: Zapfsäule 2
Eine Tankstelle informiert mit dem Aufkleber "Je Euro 73 Cent Steuern" über die Steuerbelastung beim Benzinpreis. Petra stellt fest: "Wenn der Staat überhaupt keine Steuern auf Benzin mehr erheben würde, würde der Benzinpreis auf etwa ein Viertel des jetzigen Preises sinken."
Erkläre, wie Petra zu dieser Aussage kommt.
- 1 Euro - 73 Cent = 27 Cent, das entspricht ca. 25% bzw. 1/4.
- 73 Cent pro Euro bedeutet 73% Steuern, also etwa 3/4. Also etwas 1/4 ohne Steuern.
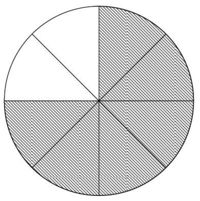
Aufgabe 5: Kreis
Wie viel Prozent des Kreises wurden eingefärbt?
Kreuze die richtige Lösung an. (!30%) (!45%) (!60%) (!70%) (75%) (!95%)
Aufgabe 6: Gleichung
Du siehst hier folgende Aufgabe: 248 + 146 + 320 =
Das Ergebnis der Aufgabe ist eine gerade Zahl.
Erkläre, warum das so ist, ohne das Ergebnis auszurechnen.
zum Beispiel:
- 248, 146, 320 sind gerade Zahlen. werden diese Zahlen addiert, dann ist auch das Ergebnis eine gerade Zahl
- In den Zahlen sind nur gerade Zahlen.
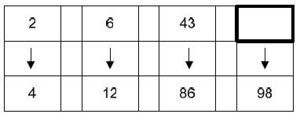
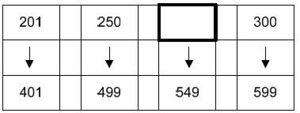
Aufgabe 7: Welche Zahl fehlt?
Trage die fehlende Zahl ein!
- 49
- 275
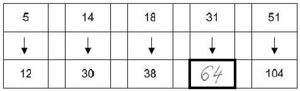
3. Timo schreibt die Zahl 64 zur 31. Das ist die richtige Lösung! Schreibe auf, wie Timo die Zahl 64 gefunden hat.
"Obere Zahl mal 2 und dann plus 2" oder "Obere Zahl plus 1 und dann mal 2"
Aufgabe 8: Ziffer 5
Peter hat nacheinander alle Zahlen von 1 bis 99 notiert.
Wie oft hat er dabei die Ziffer 5 geschrieben?
20 mal
Wie viele Ziffern hat Peter insgesamt geschrieben?
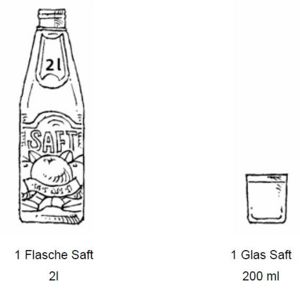
189 Ziffern
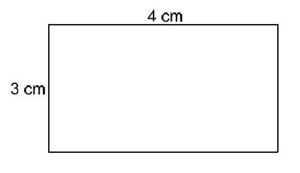
Aufgabe 9: Rechteck
Ein Rechteck ist 4 cm lang und 3 cm breit.
Wie groß ist sein Flächeninhalt?
Kreuze an.
(12cm2) (!7 cm) (!7 cm2) (!12 cm) (!14 cm)
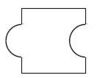
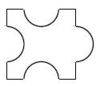
Aufgabe 10: Puzzleteile
Welches dieser Puzzleteile hat den größten Flächeninhalt? Kreuze an.
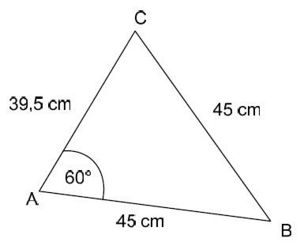
Aufgabe 12: Das unmögliche Dreieck
Begründe, warum es kein Dreieck mit diesen Maßen geben kann.
z.B.: Das Dreieck ABC ist gleichschenklig und hat einen Innenwinkel von 600. Folglich müsste dieses Dreieck gleichseitig sein. Daher müssten alle Seiten entweder 39,5 cm oder 45 cm lang sein.
Aufgabe 13: Geld umrechnen
Rechne um:
27 € 50 Cent = ..... Euro
1 € 1 Cent = ..... Cent
Aufgabe 14: Minuten und Sekunden
Rechne die Zeitangaben um und fülle die Lücken aus. Beispiel: 95 s = 1 min 35s
..... s = 3 min 28 s
136 s = ..... min ..... s
..... s = 8 min 20 s
Aufgabe 15: Fehlendes Zeichen
Ordne zu:
| < | 5m ... 5,50 m | 0, 8 cm ... 100 mm |
| > | 20 cm ... 20 mm | 700 cm ... 17 cm |
| = | 180 cm ... 1,80 m | 4 cm ... 40 mm |
Aufgabe 16: Winkel im Dreieck
In einem gleichschenkligen Dreieck ist der Winkel an der Spitze dreimal so groß wie ein Basiswinkel .
Wie groß sind die Winkel dieses Dreiecks? Kreuze die richtige Antwort an.
(!) (!) () (!)
Aufgabe 17: Nachbarseiten im Parallelogramm
Bei einem Parallelogramm ist eine Seite 40 cm lang und eine banachbarte Seite 90 cm. Wie groß ist der Umfang des Parallelogramms?
Kreuze an. (!130 cm) (!170 cm) (260 cm) (!340 cm) (!360 cm)
Aufgabe 18: Fahrplan
Hier siehst du den Fahrplan von Köln mit dem Intervity IC 800 nach Hamburg.
| Bahnhof | an | ab |
|---|---|---|
| Köln Hbf | 10:09 | |
| Düsseldorf Hbf | 10:30 | 10:32 |
| Duisburg Hbf | 10:44 | 10:46 |
| Essen Hbf | 10:57 | 10:59 |
| Bochum Hbf | 11:07 | 11:09 |
| Dortmund Hbf | 11:20 | 11:24 |
| Münster (Westf) Hbf | 11:53 | 11:55 |
| Osnabrück Hbf | 12:18 | 12:20 |
| Bremen Hbf | 13:13 | 13:15 |
| Hamburg - Harburg | 13:59 | 14:01 |
| Hamburg Hbf | 14:09 |
- Wie lange braucht der Zug von Köln bis Hamburg Hbf?
- Her Schmitz fährt von Essen nach Bremen. Wie lange braucht der Zug für diese Strecke?
- Frau Krüger fährt von Köln nach Münster. Wie lange braucht der Zug für diese Strecke?
- An welchem Bahnhof hält der Zug am längsten?
- 4 Stunden oder 240 Minuten
- 2 Stunden 14 Minuten oder 134 Minuten
- 1 Stunde 44 Minuten oder 104 Minuten
- Dortmund
Aufgabe 19: Fadenaufgabe
Ein 34 Zentimeter langer Faden wird zu einem Rechteck gelegt. Die Breite des Rechteckes beträgt 8 Zentimeter. Wie lang ist das Rechteck?
(!8 Zentimeter) (9 Zentimeter) (!13 Zentimeter) (!18 Zentimeter)
Aufgabe 20.1: Museum
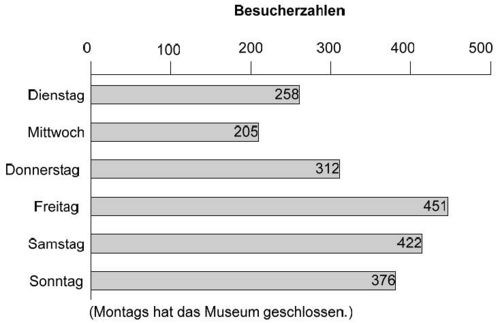
Eine neue Sonderausstellung ist eröffnet worden. Die Besucherzahlen der ersten Woche kannst du der Grafik entnehmen:
An welchem Wochentag kamen die meisten Besucher?
Freitag
Aufgabe 20.2: Museum
Bestimme mit der Grafik aus 20.1, wie viele Personen im Schnitt pro Besuchstag die Ausstellung gesehen haben.
Kreuze an, welcher Wert deinem Ergebnis am nächsten liegt.
(!289) (!328) (337) (!344) (!381)
Aufgabe 21: Körpertemperatur
Oliver liegt im Krankenhaus. Da er mit hohem Fieber eingeliefert wurde, wird mehrmals am Tag seine Körpertemperatur gemessen.
| 6 Uhr | 9 Uhr | 12 Uhr | 15 Uhr | 20 Uhr | |
|---|---|---|---|---|---|
| Sonntag | - | - | 39,80 | 39,70 | 39,90 |
| Montag | 38,50 | 38,10 | 38,00 | 38,20 | 38,50 |
| Dienstag | 37,90 | 37,90 | 38,10 | 38,30 | 38,30 |
| Mittwoch | 37,30 | 37,50 | 37,70 | 37,60 | 37,40 |
Wann wurde die höchste Temperatur gemessen? Kreuze an.
(!Montag, 6 Uhr) (!Montag, 9 Uhr) (!Dienstag, 15 Uhr) (Sonntag, 20 Uhr)
Wann wurde die niedrigste Temperatur gemessen? Kreuze an.
(!Montag, 12 Uhr) (!Dienstag, 6 Uhr) (Mittwoch, 6 Uhr) (!Mittwoch, 20 Uhr)
Aufgabe 22: Münzwurf Wenn eine Münze geworfen wird, beträgt die Wahrscheinlichkeit, dass die Zahl oben liegt, .
In drei aufeinander folgenden Würfen landet die Münze jedes Mal so, dass die Zahl oben ist. Welche der vier Aussagen trifft für den vierten Wurf zu?
Kreuze die richtige Aussage an.
(!Es ist wahrscheinlicher, dass der Adler oben liegt.) (!Es ist wahrscheinlicher, dass die Zahl oben liegt.) (Es ist gleich wahrscheinlich, dass Zahl oder Adler oben liegt.) (!Um die Frage zu beantworten, braucht man noch mehr Informationenen.)
Aufgabe 23: Spielsteine
Eine Kiste enthält 45 farbige Spielsteine: blaue, grüne und gelbe. Wenn die Wahrscheinlichkeit, einen gelben zu ziehen, beträgt, wie viele gelbe Spielsteine sind dann in der Kiste? Kreuze an.
(!2) (!5) (! 9) (18)
Aufgabe 24: Rotblauer Würfel
Jede der sechs Flächen eines Würfels ist angemalt. Einige Flächen sind rot und einige Flächen sind blau. Beim Würfeln ist die Wahrscheinlichkeit, dass eine rote Fläche oben liegen bleibt, . Wie viele Flächen des Würfels sind rot angemalt? Kreuze an.
(!eine) (!zwei) (! drei) (vier) (! fünf)
Aufgabe 25.1: Wertetabelle
Kevin berechnet folgende Wertetabelle einer linearen Funktion. Der letzte y-Wert fehlt noch.
| x | 2 | 3 | 4 | 5 | 6 |
| y | 7 | 10 | 13 | 16 | ... |
Ermittle den fehlenden y-Wert und trage ihn in die Tabelle ein.
19
Aufgabe 25.2: Wertetabelle
Welche Gleichung gehört zu der Wertetabelle, die Kevin berechnet hat (siehe Aufgabe 25.1)? Kreuze an.
(!y = x + 5) (!y = x - 5) (! y = 4x - 1) (y = 3x + 1)
Aufgabe 26: Gleichung
Gegeben ist die Gleichung 6x = 4,2. Bestimme x.
Aufgabe 27: Postkarten
Martin und Uta kaufen Postkarten. Die Postkarten haben alle den gleichen Preis. Uta kauft neun Karten, Martin kauft sechs Karten. Die Postkarten kosten zusammen 9,00€. Wie viel bezahlt Uta?
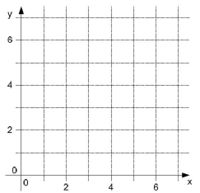
Aufgabe 28: Koordinatensystem
1. Zeichne den Punkt A (2|3) in das Koordinatensystem ein.
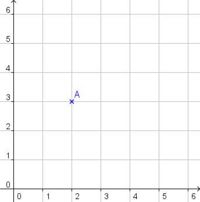
2. Trage die Koordinaten des Punktes Q ein.
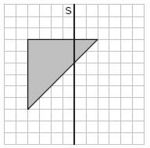
Aufgabe 29: Spiegelung
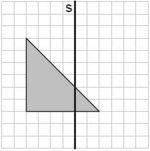 Das graue Dreieck wird an der Achse a gespiegelt.
Welche der Figuren stellt das Ergebnis der Spiegelung dar? Kreuze an.
Das graue Dreieck wird an der Achse a gespiegelt.
Welche der Figuren stellt das Ergebnis der Spiegelung dar? Kreuze an.
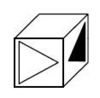
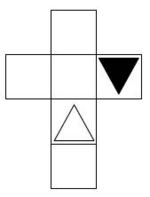
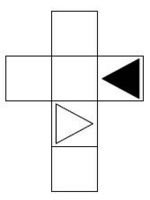
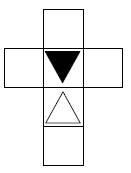
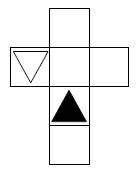
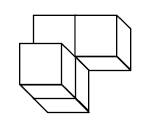
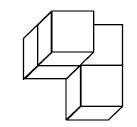
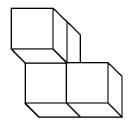
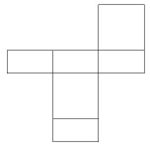
Aufgabe 30: Würfelnetze
Welches der vier Netze ergibt beim Zusammenfalten den oben abgebildeten Würfel? Kreuze an.
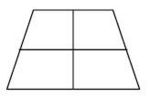
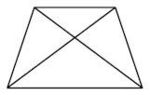
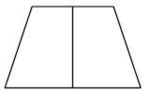
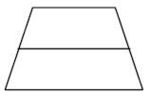
Aufgabe 31: Symmetrieachsen im Trapez
Welche Zeichnung zeigt alle Symmetrieachsen eines gleichschenkligen (symmetrischen) Trapezes? Kreuze an.
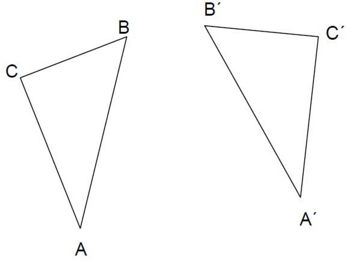
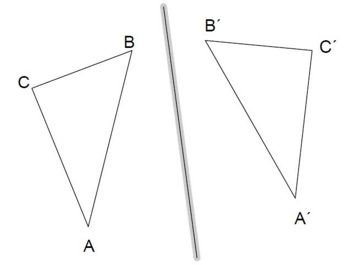
Aufgabe 32: Spiegelachse
Das Dreieck A'B'C' ist das Ergebnis einer Achsenspiegelung des Dreiecks ABC.
Zeichne die Spiegelachse g ein.
Aufgabe 33: Parallelogramme
Welche dieser Aussagen, die für alle Parallelogramme gelten sollen, ist FALSCH?
Kreuze an.
(!Gegenüberliegende Seiten sind parallel.) (!Die Diagonalen halbieren sich gegenseitig.) (!Gegenüberliegende Winkel sind gleich groß.) (Es gibt genau eine Spiegelachse.) (!Gegenüberliegende Seiten sind gleich lang.)
Aufgabe 34: Kongruente Figuren
Welche der unten stehenden Figuren ist nicht kongruent (deckungsgleich) zu der oben gegebenen Figur?
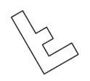
Aufgabe 35: Würfel drehen
Dieser Körper wird in eine andere Lage gedreht:
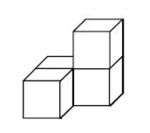
Welches der folgenden Bilder zeigt den gedrehten Körper? Kreuze an.
Aufgabe 36: Spiegelschrift
Du hältst dieses Schild so vor dich, dass jeder es lesen kann, und stehst vor einem Spiegel. Was siehst du? Kreuze an.
Aufgabe 37: Quadernetze
Welches der vier Netze ergibt beim Zusammenfalten keinen Quader? Kreuze an.
Aufgabe 38: Gleichschenklige Dreiecke
Sind folgende Aussagen wahr oder falsch?
Jedes gleichschenklige Dreieck ...
| wahr | ... besitzt mindestens eine Symmetrieachse. | ... hat mindestens zwei gleich große Winkel. |
| falsch | ...besitzt drei gleich lange Seiten. | ... hat immer einen rechten Winkel. |
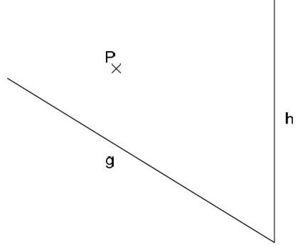
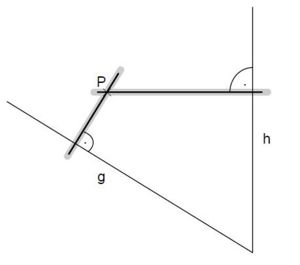
Aufgabe 39: Punkte und Abstände
Gegeben sind zwei Halbgeraden g und h und ein Punkt P.
Zeichne eine Senkrechte durch den Punkt P auf die Halbgerade g und eine Senkrechte durch den Punkt P auf die Halbgerade h.
Aufgabe 40: Dreieck
In einem gleichschenkligen Dreieck ist die Basis doppelt so lang wie die Höhe. Wie groß sind die Winkel dieses Dreiecks?
450, 450 und 900