Prozente und Prozentrechnung

Lernpfad

Herzlich willkommen im Lernpfad Prozente und Prozentrechnung!

Dieser Lernpfad soll dir dabei helfen, dein Wissen aus der Bruchrechnung auf die Prozentrechnung zu übertragen und deine Vorstellung von Prozenten auf- bzw. auszubauen.

Das Schöne daran ist, dass du vieles von dem, was du bereits aus der Bruchrechnung kennst, hier direkt anwenden kannst.

Am Ende dieses Lernpfades sollst du

• den Zusammenhang zwischen Brüchen und Prozenten kennen
• einfache Prozentaufgaben lösen können
• mit dem Prozentstreifen umgehen können
• die Fachbegriffe zur Prozentrechnung kennengelernt haben

Merke

Der Begriff "Prozent" heißt dabei nichts anderes als "von Hundert". Du hast es also im Prinzip mit nichts anderem zu tun, als einem Bruch, dessen Nenner immer 100 ist. Hier lernst du, wie du dein Wissen aus der Bruchrechnung in die Prozentrechnung übertragen kannst!

Also: Leg los!

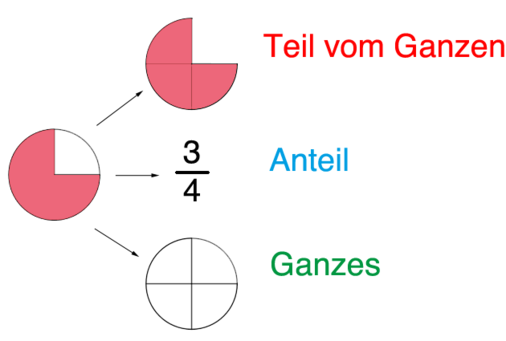
Wiederholung: Bruchteil, Anteil und Ganzes

Info

Zunächst rufen wir uns in Erinnerung, was der Bruchteil, der Anteil und das Ganze in der Bruchrechnung war. Im Rahmen der Bruchrechnung hast du schon einige Beispiele von Prozentsätzen kennengelernt. Wir schauen uns zunächst noch einmal die Begriffe aus der Bruchrechnung an!

Beispiel

In diesem Beispiel schauen wir uns noch einmal drei Viertel eines Kreises an.

Um einen Anteil nun in der Prozentschreibweise schreiben zu können, musst du den Bruch zunächst in einen Bruch mit dem Nenner 100 umwandeln, indem du ihn entsprechend erweiterst oder kürzt.

Brüche und Prozentsätze zuordnen

Üben

Zunächst siehst du in der folgenden Aufgabe einige Formen, von denen bestimmte Anteile farbig markiert sind. Gib die farbigen Anteile sowohl in der Bruch- als auch in der Prozentschreibweise an!
Wenn du mit einer Teilaufgabe fertig bist, kannst du mit dem Pfeil oben links zurück in das Menü gelangen.

Üben

In der folgenden Aufgabe siehst du einige Brüche und Prozentsätze, die du bestimmt schon kennst. Ordne den Brüche die entsprechenden Prozentsätze zu und überprüfe deine Ergebnisse am Ende mit einem Klick auf den blauen Haken unten rechts!

Üben

Ein wenig schwieriger wird es in der nächsten Aufgabe. Hier sollst du nun ohne Vorgabe von Werten die richtigen Prozentsätze in die Felder eintragen. Viel Erfolg!
Tipp: Bei einigen Aufgaben findest du oben links ein kleines Glühbirnensymbol. Solltest du beim Lösen der Aufgaben Hilfe benötigen, so erhältst du durch einen Klick darauf einen Hinweis!

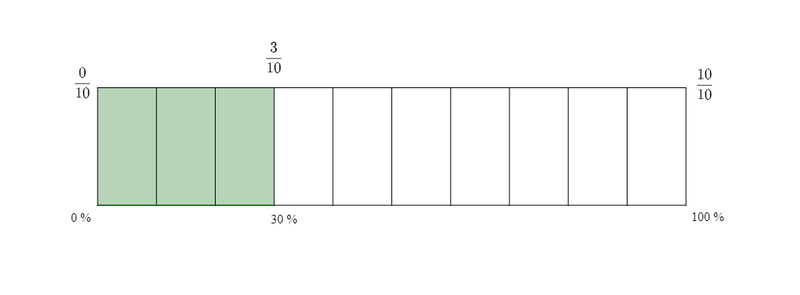
Arbeiten mit dem Bruch- und Prozentstreifen

Info

Bestimmt kennst du aus der Bruchrechnung noch Übungsmaterial Material wie z.B. den Bruchstreifen.
In der Prozentrechnung arbeitet man am besten mit dem Prozentstreifen.
Direkt unter diesem Text findest du einen interaktive Bruch- und Prozentstreifen, an denen du zunächst frei experimentieren kannst.
Wenn du den Mauszeiger auf das Fenster mit den Streifen führst, kannst du mit dem Mausrad auch weiter hinauszoomen, falls das Fenster für einen länger eingestellten Streifen zu klein sein sollte.

Üben

Zeichne dir nun einen solchen Prozentstreifen in dein Heft! Nutze dafür den Bruch 3/10 und ermittle die entsprechende Prozentschreibweise!
Du kannst deinen Prozentstreifen anschließend mit der Musterlösung vergleichen, indem du auf "Lösung anzeigen" klickst!

Üben

Bestimme nun mit dem interaktiven Bruch- und Prozentstreifen 2/5 von 120 kg!

Üben

Bestimme in dieser Aufgabe nun 3/10 von 150 m!

Üben

Versuche nun, die folgenden Aufgaben zu lösen. Du kannst dafür immer auf den interaktiven Bruch- und Prozentstreifen zurückgreifen!

Merke

In diesem Beispiel schauen wir uns noch einmal drei Viertel eines Kreises an.

In der Prozentrechnung gibt es nun andere Begriffe für das, was du bereits aus der Bruchrechnung kennst.
Das Ganze nennt sich hier der Grundwert (abgekürzt mit einem großen G), der Bruchteil entspricht dem Prozentwert (abgekürzt mit einem großen W) und der Anteil wird hier Prozentsatz (kurz p %)" genannt und nicht mehr als Bruch, sondern als Zahlenwert mit einem Prozentzeichen (%) dahinter angegeben.

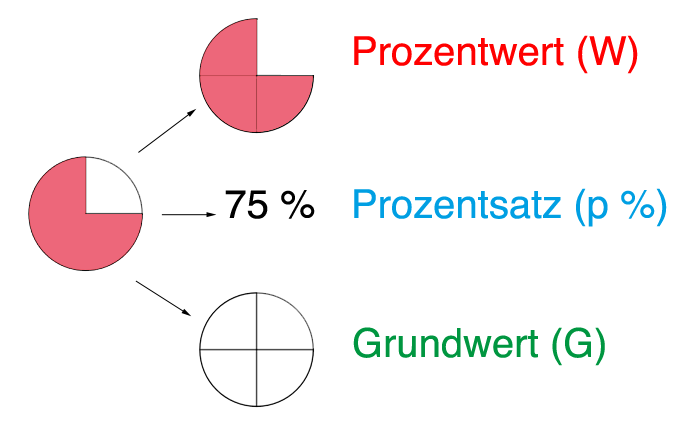
Den Prozentwert berechnen

Lückentext

Versuche zur Verinnerlichung nun, diesen Lückentext auszufüllen. Klicke dafür einfach in die entsprechenden Lückenfelder und wähle den Begriff aus, den du für richtig hältst. Überprüfe am Ende deine Eingaben durch einen Klick auf den blauen Haken unten rechts!