Größenvergleich von Brüchen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 63: | Zeile 63: | ||
|}--> | |}--> | ||
<br> | <br> | ||
<ggb_applet height="450" width=" | <ggb_applet height="450" width="700" id="vztvat2r" /> | ||
Waren deine Antworten richtig? Teste dich: | Waren deine Antworten richtig? Teste dich: | ||
Version vom 8. Oktober 2020, 10:00 Uhr
Station 1.Regel
Regel für Stammbrüche
- Damit du Brüche vergleichen kannst, gibt es drei Regeln, die dir dabei helfen können.
Aber gilt das nur für Stammbrüche?
Finde eine Regel
- Bearbeite nun folgende Aufgaben und schreibe dir deine Antworten auf deinen Laufzettel,
du wirst sie noch kontrollieren müssen.
- Verstelle wieder zuerst den Nenner und dann den Zähler.
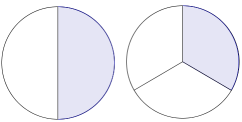
- Stelle den Bruch und ein. Welcher Bruch ist größer?
- Das Bruchpaar und hat den gleichen Zähler.
Vergleiche den Nenner des größeren mit dem Nenner des kleineren Bruches.

Waren deine Antworten richtig? Teste dich:
- ist der größere Bruch.
- Der Nenner des größeres Bruches ist kleiner als der Nenner des kleineren Bruches .
Die 1.Regel
Die Vermutung gilt also für alle Brüche, die einen gleichen Zähler haben.
Schreibe dir den Merksatz in dein Heft:
Station 2.Regel
Finde eine Regel
Verstelle wieder zuerst den Nenner und dann den Zähler.
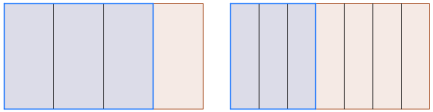
- Stelle den Bruch und ein. Welcher Bruch ist größer?
- Das Bruchpaar und hat den gleichen Nenner.
Vergleiche den Zähler des größeren mit dem Zähler des kleineren Bruches.

Waren deine Antworten richtig? Teste dich:
- ist der größere Bruch.
- Der Zähler des größeres Bruches ist größer als der Zähler des kleineren Bruches .
Die 2.Regel
Schreibe dir den Merksatz in dein Heft:
Station 3.Regel
Finde eine letzte Regel
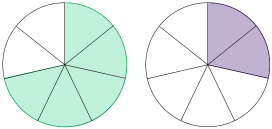
- Stelle den Bruch und ein. Welcher Bruch ist größer?
- Stelle den Bruch und ein. Welcher Bruch ist größer?

Waren deine Antworten richtig? Teste dich:
- ist der größere Bruch.
- ist der größere Bruch.
Aber da steckt doch keine Regel dahinter, oder?
Der Hauptnenner
- Schreibe dir den Merksatz in dein Heft:
Es gibt schon eine Regel für Brüche, die den gleichen Nenner haben: Die 2.Regel!
Die 3.Regel
- Schreibe dir den Merksatz in dein Heft:
Sind weder die Zähler noch die Nenner gleich, dann musst du die Brüche gleichnamig machen.
Wenn sie dann den gleichen Nenner, z.B. den Hauptnenner haben, kannst du die 2.Regel anwenden.
Der Bruch mit dem größeren Zähler ist größer.
Beispiel:
- Die beiden Brüche haben den Hauptnenner 18.
- Durch Erweitern auf den Hauptnenner, siehst du, dass und ist.
- Nach der 2.Regel weißt du, dass . Also ist .
Übungen zum Hauptnenner und zum Größenvergleich
Es gibt mehrere Aufgaben und Schwierigkeiten zur Auswahl. Wir empfehlen dir: Wähle zwei Übungen aus der Schwierigkeitsstufe "leicht" und "mittelschwer" aus, die du bearbeitest. Danach teste dich mit der Übung aus der Schwierigkeitsstufe "schwer".
MITTELSCHWER
<metakeywords>ZUM2Edutags,ZUM-Wiki,Größenvergleich von Brüchen,Mathematik-digital, Lernpfad, Bruch, Brüche, Bruchrechnung, Größenvergleich, interaktive Übungen, Mathematik, 6. Klasse</metakeywords>