Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Benutzer:PascalHänle/Folgen und Grenzwert: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|Aufgabe 2|'''a)''' Beschreibe die folgenden Folgen anhand des Applets für wachsende Patznummer n? Beschreibe die Gemeinsamkeiten und Unterschiede der vier Folgen. | {{Box|Aufgabe 2|'''a)''' Beschreibe die folgenden Folgen anhand des Applets für wachsende Patznummer n? Beschreibe die Gemeinsamkeiten und Unterschiede der vier Folgen. <br/> | ||
a_n | a_n https://www.geogebra.org/classic/bmcadppf <br/> | ||
b_n | b_n https://www.geogebra.org/classic/rdrfpfja<br/> | ||
c_n | c_n https://www.geogebra.org/classic/zcagqxnk<br/> | ||
d_n | d_n https://www.geogebra.org/classic/qb9zrvfn<br/> | ||
Version vom 13. September 2020, 17:32 Uhr
Folgen und Grenzwerte
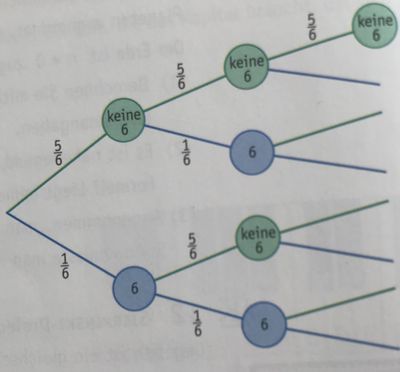
Beim Spiel Mensch ärgere Dich nicht benötigt man eine 6 um mit dem ersten Männchen ins Spiel einzusteigen.
Aufgabe 1
a) Wie groß ist die Wahrscheinlichkeit, dass drei Würfe, vier Würfe, fünf Würfe, …, n Würfe genügen, um ins Spiel zu kommen. Stelle hierzu eine Folge in expliziter Schreibweise auf.
Aufgabe 2
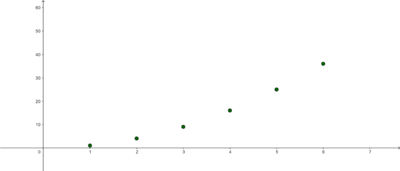
a) Beschreibe die folgenden Folgen anhand des Applets für wachsende Patznummer n? Beschreibe die Gemeinsamkeiten und Unterschiede der vier Folgen.
a_n https://www.geogebra.org/classic/bmcadppf
b_n https://www.geogebra.org/classic/rdrfpfja
c_n https://www.geogebra.org/classic/zcagqxnk
d_n https://www.geogebra.org/classic/qb9zrvfn
Aufgabe 3
Fasse Deine Erkenntnis aus Aufgabe 1 und 2 zusammen und formuliere eine Eigenschaft für Folgen wie aus Aufgabe 1 und 2.